Difference between revisions of "99 questions/70B to 73"
RossPaterson (talk | contribs) m (move data definition into 70C) |
m |
||
| (10 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
__NOTOC__ |
__NOTOC__ |
||
| − | This is part of [[H-99:_Ninety-Nine_Haskell_Problems|Ninety-Nine Haskell Problems]], based on [ |
+ | This is part of [[H-99:_Ninety-Nine_Haskell_Problems|Ninety-Nine Haskell Problems]], based on [https://prof.ti.bfh.ch/hew1/informatik3/prolog/p-99/ Ninety-Nine Prolog Problems]. |
| − | = |
+ | <h2 style="border:none">Multiway Trees</h2> |
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest. |
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest. |
||
| − | + | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p70.gif |
|
== Problem 70B == |
== Problem 70B == |
||
| + | <div style="border-bottom:1px solid #eee">(*) Check whether a given term represents a multiway tree. <span style="float:right"><small>(no solution needed)</small></span> |
||
| − | |||
| + | </div> |
||
| − | (*) Check whether a given term represents a multiway tree. |
||
| + | <br> |
||
In Prolog or Lisp, one writes a predicate to check this. |
In Prolog or Lisp, one writes a predicate to check this. |
||
Example in Prolog: |
Example in Prolog: |
||
| + | |||
<pre> |
<pre> |
||
?- istree(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])). |
?- istree(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])). |
||
| Line 21: | Line 23: | ||
</pre> |
</pre> |
||
| − | In Haskell, we define multiway trees as a datatype, as in the module [http://www.haskell.org/ghc/docs/latest/html/libraries/ |
+ | In Haskell, we define multiway trees as a datatype, as in the module [http://www.haskell.org/ghc/docs/latest/html/libraries/containers/Data-Tree.html Data.Tree]: |
| + | |||
<haskell> |
<haskell> |
||
data Tree a = Node a [Tree a] |
data Tree a = Node a [Tree a] |
||
deriving (Eq, Show) |
deriving (Eq, Show) |
||
</haskell> |
</haskell> |
||
| + | |||
Some example trees: |
Some example trees: |
||
| + | |||
<haskell> |
<haskell> |
||
tree1 = Node 'a' [] |
tree1 = Node 'a' [] |
||
| Line 42: | Line 47: | ||
] |
] |
||
</haskell> |
</haskell> |
||
| + | |||
The last is the tree illustrated above. |
The last is the tree illustrated above. |
||
| − | As in |
+ | As in Problem 54A, all members of this type are multiway trees; there is no use for a predicate to test them. |
| + | |||
| − | there is no use for a predicate to test them. |
||
== Problem 70C == |
== Problem 70C == |
||
| + | <div style="border-bottom:1px solid #eee">(*) Count the nodes of a multiway tree. <span style="float:right"><small>[[99 questions/Solutions/70C|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | (*) Count the nodes of a multiway tree. |
||
| + | <br> |
||
Example in Haskell: |
Example in Haskell: |
||
| − | <pre> |
||
| − | Tree> nnodes tree2 |
||
| − | 2 |
||
| − | </pre> |
||
| − | Solution: |
||
<haskell> |
<haskell> |
||
| − | nnodes |
+ | λ> nnodes tree2 |
| + | 2 |
||
| − | nnodes (Node _ ts) = 1 + sum (map nnodes ts) |
||
</haskell> |
</haskell> |
||
| − | == Problem 70 == |
||
| + | == Problem 70 == |
||
| − | (**) Tree construction from a node string. |
||
| + | <div style="border-bottom:1px solid #eee">(**) Construct a multiway tree from a node string. <span style="float:right"><small>[[99 questions/Solutions/70|Solutions]]</small></span> |
||
| + | </div> |
||
| + | <br> |
||
We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level. |
We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level. |
||
| Line 71: | Line 75: | ||
By this rule, the tree below (<tt>tree5</tt>) is represented as: <tt>afg^^c^bd^e^^^</tt> |
By this rule, the tree below (<tt>tree5</tt>) is represented as: <tt>afg^^c^bd^e^^^</tt> |
||
| − | + | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p70.gif |
|
Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. |
Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. |
||
Make your predicate work in both directions. |
Make your predicate work in both directions. |
||
| + | Example in Haskell: |
||
| − | Solution: |
||
| − | We could write separate printing and parsing functions, but the problem statement asks for a bidirectional function. |
||
| − | First we need a parser monad, with some primitives: |
||
<haskell> |
<haskell> |
||
| + | λ> stringToTree "afg^^c^bd^e^^^" |
||
| − | newtype P a = P { runP :: String -> Maybe (a, String) } |
||
| + | Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]] |
||
| + | λ> treeToString (Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]]) |
||
| − | instance Monad P where |
||
| + | "afg^^c^bd^e^^^" |
||
| − | return x = P $ \ s -> Just (x, s) |
||
| − | P v >>= f = P $ \ s -> do |
||
| − | (x, s') <- v s |
||
| − | runP (f x) s' |
||
| − | instance MonadPlus P where |
||
| − | mzero = P $ \ _ -> Nothing |
||
| − | P u `mplus` P v = P $ \ s -> u s `mplus` v s |
||
| − | |||
| − | charP :: P Char |
||
| − | charP = P view_list |
||
| − | where view_list [] = Nothing |
||
| − | view_list (c:cs) = Just (c, cs) |
||
| − | |||
| − | literalP :: Char -> P () |
||
| − | literalP c = do { c' <- charP; guard (c == c') } |
||
| − | |||
| − | spaceP :: P () |
||
| − | spaceP = P (\ s -> Just ((), dropWhile isSpace s)) |
||
</haskell> |
</haskell> |
||
| − | Next a <tt>Syntax</tt> type, combining printing and parsing functions: |
||
| − | <haskell> |
||
| − | data Syntax a = Syntax { |
||
| − | display :: a -> String, |
||
| − | parse :: P a |
||
| − | } |
||
| − | </haskell> |
||
| − | (We don't use a class, because we want multiple syntaxes for a given type.) |
||
| − | Some combinators for building syntaxes: |
||
| − | <haskell> |
||
| − | -- concatenation |
||
| − | (<*>) :: Syntax a -> Syntax b -> Syntax (a,b) |
||
| − | a <*> b = Syntax { |
||
| − | display = \ (va,vb) -> display a va ++ display b vb, |
||
| − | parse = liftM2 (,) (parse a) (parse b) |
||
| − | } |
||
| − | -- alternatives |
||
| − | (<|>) :: Syntax a -> Syntax b -> Syntax (Either a b) |
||
| − | a <|> b = Syntax { |
||
| − | display = either (display a) (display b), |
||
| − | parse = liftM Left (parse a) `mplus` liftM Right (parse b) |
||
| − | } |
||
| − | |||
| − | char :: Syntax Char |
||
| − | char = Syntax return charP |
||
| − | |||
| − | literal :: Char -> Syntax () |
||
| − | literal c = Syntax (const [c]) (literalP c) |
||
| − | |||
| − | space :: Syntax () |
||
| − | space = Syntax (const " ") spaceP |
||
| − | |||
| − | iso :: (a -> b) -> (b -> a) -> Syntax a -> Syntax b |
||
| − | iso a_to_b b_to_a a = Syntax { |
||
| − | display = display a . b_to_a, |
||
| − | parse = liftM a_to_b (parse a) |
||
| − | } |
||
| − | </haskell> |
||
| − | The last one maps a syntax using an isomorphism between types. |
||
| − | Some uses of this function: |
||
| − | <haskell> |
||
| − | -- concatenation, with no value in the first part |
||
| − | (*>) :: Syntax () -> Syntax a -> Syntax a |
||
| − | p *> q = iso snd ((,) ()) (p <*> q) |
||
| − | |||
| − | -- list of a's, followed by finish |
||
| − | list :: Syntax a -> Syntax () -> Syntax [a] |
||
| − | list a finish = iso toList fromList (finish <|> (a <*> list a finish)) |
||
| − | where toList (Left _) = [] |
||
| − | toList (Right (x, xs)) = x:xs |
||
| − | fromList [] = Left () |
||
| − | fromList (x:xs) = Right (x, xs) |
||
| − | </haskell> |
||
| − | Now we can define the syntax of depth-first presentations: |
||
| − | <haskell> |
||
| − | df :: Syntax (Tree Char) |
||
| − | df = iso toTree fromTree (char <*> list df (literal '^')) |
||
| − | where toTree (x, ts) = Node x ts |
||
| − | fromTree (Node x ts) = (x, ts) |
||
| − | </haskell> |
||
| − | We are using the isomorphism between <tt>Tree a</tt> and <tt>(a, [Tree a])</tt>. |
||
| − | Some examples: |
||
| − | <pre> |
||
| − | Tree> display df tree5 |
||
| − | "afg^^c^bd^e^^^" |
||
| − | Tree> runP (parse df) "afg^^c^bd^e^^^" |
||
| − | Just (Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]],"") |
||
| − | </pre> |
||
== Problem 71 == |
== Problem 71 == |
||
| + | <div style="border-bottom:1px solid #eee">(*) Determine internal path length of multiway tree. <span style="float:right"><small>[[99 questions/Solutions/71|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | (*) Determine the internal path length of a tree. |
||
| + | <br> |
||
We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree. By this definition, <tt>tree5</tt> has an internal path length of 9. |
We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree. By this definition, <tt>tree5</tt> has an internal path length of 9. |
||
Example in Haskell: |
Example in Haskell: |
||
| + | |||
| − | <pre> |
||
| + | <haskell> |
||
| − | Tree> ipl tree5 |
||
| + | λ> ipl tree5 |
||
9 |
9 |
||
| − | + | λ> ipl tree4 |
|
2 |
2 |
||
| − | </pre> |
||
| − | |||
| − | Solution: |
||
| − | <haskell> |
||
| − | ipl :: Tree a -> Int |
||
| − | ipl = ipl' 0 |
||
| − | where ipl' d (Node _ ts) = d + sum (map (ipl' (d+1)) ts) |
||
</haskell> |
</haskell> |
||
| + | |||
== Problem 72 == |
== Problem 72 == |
||
| + | <div style="border-bottom:1px solid #eee">(*) Construct bottom-up order sequence of multiway tree nodes. <span style="float:right"><small>[[99 questions/Solutions/72|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | (*) Construct the bottom-up order sequence of the tree nodes. |
||
| + | <br> |
||
Write a predicate bottom_up(Tree,Seq) which constructs the bottom-up sequence of the nodes of the multiway tree Tree. |
Write a predicate bottom_up(Tree,Seq) which constructs the bottom-up sequence of the nodes of the multiway tree Tree. |
||
Example in Haskell: |
Example in Haskell: |
||
| − | <pre> |
||
| − | Tree> bottom_up tree5 |
||
| − | "gfcdeba" |
||
| − | </pre> |
||
| − | Solution: |
||
<haskell> |
<haskell> |
||
| − | bottom_up |
+ | λ> bottom_up tree5 |
| + | "gfcdeba" |
||
| − | bottom_up (Node x ts) = concatMap bottom_up ts ++ [x] |
||
| − | </haskell> |
||
| − | A more efficient version using an accumulator: |
||
| − | <haskell> |
||
| − | bottom_up :: Tree a -> [a] |
||
| − | bottom_up t = bottom_up_aux t [] |
||
| − | where bottom_up_aux :: Tree a -> [a] -> [a] |
||
| − | bottom_up_aux (Node x ts) xs = foldr bottom_up_aux (x:xs) ts |
||
</haskell> |
</haskell> |
||
| + | |||
== Problem 73 == |
== Problem 73 == |
||
| + | <div style="border-bottom:1px solid #eee">(**) Lisp-like multiway tree representation. <span style="float:right"><small>[[99 questions/Solutions/73|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | (**) Lisp-like tree representation. |
||
| + | <br> |
||
There is a particular notation for multiway trees in Lisp. Lisp is a prominent functional programming language, which is used primarily for artificial intelligence problems. As such it is one of the main competitors of Prolog. In Lisp almost everything is a list, just as in Prolog everything is a term. |
There is a particular notation for multiway trees in Lisp. Lisp is a prominent functional programming language, which is used primarily for artificial intelligence problems. As such it is one of the main competitors of Prolog. In Lisp almost everything is a list, just as in Prolog everything is a term. |
||
| Line 228: | Line 133: | ||
The following pictures show how multiway tree structures are represented in Lisp. |
The following pictures show how multiway tree structures are represented in Lisp. |
||
| − | + | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p73.png |
|
Note that in the "lispy" notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The "lispy" representation of a multiway tree is a sequence of atoms and parentheses '(' and ')', which we shall collectively call "tokens". We can represent this sequence of tokens as a Prolog list; e.g. the lispy expression (a (b c)) could be represented as the Prolog list ['(', a, '(', b, c, ')', ')']. Write a predicate tree_ltl(T,LTL) which constructs the "lispy token list" LTL if the tree is given as term T in the usual Prolog notation. |
Note that in the "lispy" notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The "lispy" representation of a multiway tree is a sequence of atoms and parentheses '(' and ')', which we shall collectively call "tokens". We can represent this sequence of tokens as a Prolog list; e.g. the lispy expression (a (b c)) could be represented as the Prolog list ['(', a, '(', b, c, ')', ')']. Write a predicate tree_ltl(T,LTL) which constructs the "lispy token list" LTL if the tree is given as term T in the usual Prolog notation. |
||
| Line 235: | Line 140: | ||
Example in Haskell: |
Example in Haskell: |
||
| + | |||
| − | <pre> |
||
| + | <haskell> |
||
| − | Tree> display lisp tree1 |
||
| + | λ> display lisp tree1 |
||
"a" |
"a" |
||
| − | + | λ> display lisp tree2 |
|
"(a b)" |
"(a b)" |
||
| − | + | λ> display lisp tree3 |
|
"(a (b c))" |
"(a (b c))" |
||
| − | + | λ> display lisp tree4 |
|
"(b d e)" |
"(b d e)" |
||
| − | + | λ> display lisp tree5 |
|
"(a (f g) c (b d e))" |
"(a (f g) c (b d e))" |
||
| − | </ |
+ | </haskell> |
As a second, even more interesting exercise try to rewrite tree_ltl/2 in a way that the inverse conversion is also possible. |
As a second, even more interesting exercise try to rewrite tree_ltl/2 in a way that the inverse conversion is also possible. |
||
| − | Solution: |
||
| − | using the <tt>Syntax</tt> type used in problem 70 above: |
||
| − | <haskell> |
||
| − | lisp :: Syntax (Tree Char) |
||
| − | lisp = iso toTree fromTree |
||
| − | (literal '(' *> (char <*> list (space *> lisp) (literal ')')) <|> char) |
||
| − | where toTree (Left (x, ts)) = Node x ts |
||
| − | toTree (Right x) = Node x [] |
||
| − | fromTree (Node x []) = Right x |
||
| − | fromTree (Node x ts) = Left (x, ts) |
||
| − | </haskell> |
||
| − | Here we use the isomorphism between <tt>Tree a</tt> and <tt>Either (a, [Tree a]) a</tt>, where the list is non-empty. |
||
[[Category:Tutorials]] |
[[Category:Tutorials]] |
||
Latest revision as of 05:50, 11 June 2023
This is part of Ninety-Nine Haskell Problems, based on Ninety-Nine Prolog Problems.
Multiway Trees
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.
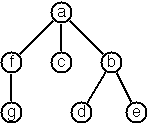
Problem 70B
In Prolog or Lisp, one writes a predicate to check this.
Example in Prolog:
?- istree(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])). Yes
In Haskell, we define multiway trees as a datatype, as in the module Data.Tree:
data Tree a = Node a [Tree a]
deriving (Eq, Show)
Some example trees:
tree1 = Node 'a' []
tree2 = Node 'a' [Node 'b' []]
tree3 = Node 'a' [Node 'b' [Node 'c' []]]
tree4 = Node 'b' [Node 'd' [], Node 'e' []]
tree5 = Node 'a' [
Node 'f' [Node 'g' []],
Node 'c' [],
Node 'b' [Node 'd' [], Node 'e' []]
]
The last is the tree illustrated above.
As in Problem 54A, all members of this type are multiway trees; there is no use for a predicate to test them.
Problem 70C
Example in Haskell:
λ> nnodes tree2
2
Problem 70
We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level.
By this rule, the tree below (tree5) is represented as: afg^^c^bd^e^^^

Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. Make your predicate work in both directions.
Example in Haskell:
λ> stringToTree "afg^^c^bd^e^^^"
Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]]
λ> treeToString (Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]])
"afg^^c^bd^e^^^"
Problem 71
We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree. By this definition, tree5 has an internal path length of 9.
Example in Haskell:
λ> ipl tree5
9
λ> ipl tree4
2
Problem 72
Write a predicate bottom_up(Tree,Seq) which constructs the bottom-up sequence of the nodes of the multiway tree Tree.
Example in Haskell:
λ> bottom_up tree5
"gfcdeba"
Problem 73
There is a particular notation for multiway trees in Lisp. Lisp is a prominent functional programming language, which is used primarily for artificial intelligence problems. As such it is one of the main competitors of Prolog. In Lisp almost everything is a list, just as in Prolog everything is a term.
The following pictures show how multiway tree structures are represented in Lisp.
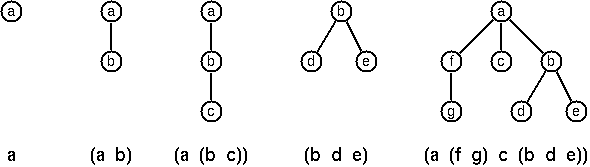
Note that in the "lispy" notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The "lispy" representation of a multiway tree is a sequence of atoms and parentheses '(' and ')', which we shall collectively call "tokens". We can represent this sequence of tokens as a Prolog list; e.g. the lispy expression (a (b c)) could be represented as the Prolog list ['(', a, '(', b, c, ')', ')']. Write a predicate tree_ltl(T,LTL) which constructs the "lispy token list" LTL if the tree is given as term T in the usual Prolog notation.
(The Prolog example given is incorrect.)
Example in Haskell:
λ> display lisp tree1
"a"
λ> display lisp tree2
"(a b)"
λ> display lisp tree3
"(a (b c))"
λ> display lisp tree4
"(b d e)"
λ> display lisp tree5
"(a (f g) c (b d e))"
As a second, even more interesting exercise try to rewrite tree_ltl/2 in a way that the inverse conversion is also possible.