Category theory/Natural transformation

Example: maybeToList

 map even $ maybeToList $ Just 5

yields the same as

 maybeToList $ fmap even $ Just 5

yields: both yield

 [False]

Commutative diagram

• Let $\mathcal{C}$, $\mathcal{D}$ denote categories.
• Let $\mathrm{\Phi },\mathrm{\Psi }:\mathcal{C}\to \mathcal{D}$ be functors.
• Let $X,Y\in \mathbf{O}\mathbf{b}(\mathcal{C})$. Let $f\in {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathcal{C}}(X,Y)$.

Let us define the $\eta :\mathrm{\Phi }\to \mathrm{\Psi }$ natural transformation. It associates to each object of $\mathcal{C}$ a morphism of $\mathcal{D}$ in the following way (usually, not sets are discussed here, but proper classes, so I do not use term “function” for this $\mathbf{O}\mathbf{b}(\mathcal{C})\to \mathbf{M}\mathbf{o}\mathbf{r}(\mathcal{D})$ mapping):

• $\mathrm{\forall }A\in \mathbf{O}\mathbf{b}(\mathcal{C})⟼{\eta }_A\in {\mathrm{H}\mathrm{o}\mathrm{m}}_{\mathcal{D}}(\mathrm{\Phi }(A),\mathrm{\Psi }(A))$. We call ${\eta }_A$ the component of $\eta$ at A.
• ${\eta }_Y\cdot \mathrm{\Phi }(f)=\mathrm{\Psi }(f)\cdot {\eta }_X$

Thus, the following diagram commutes (in $\mathcal{D}$):

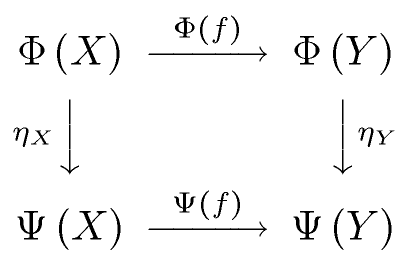
Vertical arrows: sides of objects

… showing how the natural transformation works.

$\eta :\mathrm{\Phi }\to \mathrm{\Psi }$

maybeToList :: Maybe a -> [a]

Left: side of X object

${\eta }_X:\mathrm{\Phi }(X)\to \mathrm{\Psi }(X)$

	maybeToList :: Maybe Int -> [Int]
Nothing	[]
Just 0	[0]
Just 1	[1]

Right: side of Y object

${\eta }_Y:\mathrm{\Phi }(Y)\to \mathrm{\Psi }(Y)$

	maybeToList :: Maybe Bool -> [Bool]
Nothing	[]
Just True	[True]
Just False	[False]

Horizontal arrows: sides of functors

$f:X\to Y$

 even :: Int -> Bool

Side of $\mathrm{\Phi }$ functor

$\mathrm{\Phi }(f):\mathrm{\Phi }(X)\to \mathrm{\Phi }(Y)$

	fmap even:: Maybe Int -> Maybe Bool
Nothing	Nothing
Just 0	Just True
Just 1	Just False

Side of $\mathrm{\Psi }$ functor

$\mathrm{\Psi }(f):\mathrm{\Psi }(X)\to \mathrm{\Psi }(Y)$

	map even:: [Int] -> [Bool]
[]	[]
[0]	[True]
[1]	[False]

Commutativity of the diagram

$\mathrm{\Psi }(f)\cdot {\eta }_X={\eta }_Y\cdot \mathrm{\Phi }(f)$

both paths span between

$\mathrm{\Phi }(X)\to \mathrm{\Psi }(Y)$

	Maybe Int -> [Bool]
	map even . maybeToList	maybeToList . fmap even
Nothing	[]	[]
Just 0	[True]	[True]
Just 1	[False]	[False]

Remarks

• even has a more general type (Integral a => a -> Bool) than described here
• Words “side”, “horizontal”, “vertical”, “left”, “right” serve here only to point to the discussed parts of a diagram, thus, they are not part of the scientific terminology.
• If You want to modifiy the #Commutative diagram, see its source code (in LaTeX using amscd).

External links

• The corresponding HaWiki article is not migrated here yet, so You can see it for more information.
• Wikipedia's Natural transformation article