Difference between revisions of "IcoGrid"
| (6 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
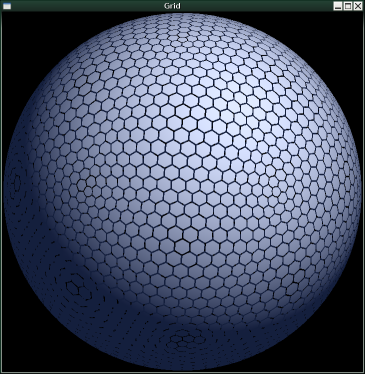
It's easier to show than to describe, so here is a screenshot of an OpenGL application I wrote to render a grid generated by IcoGrid: |
It's easier to show than to describe, so here is a screenshot of an OpenGL application I wrote to render a grid generated by IcoGrid: |
||
| − | [[Image:IcoGrid.png]] |
+ | [[Image:IcoGrid-small.png]] |
| + | |||
| + | ==Grid Overview== |
||
| + | |||
| + | The grid is layed out as twenty triangular hexagon grids fitted together to make an icosahedron. The points where file of these triangular grids meet are pentagons. The size of the grid is length of one of the sides of the triangular grids. Thus a grid of size S will have approximately (S^2)*10 cells. |
||
| + | |||
| + | Most of the library functions require the grid size as the first parameter. Cells are identified by integers from [0..N-1] for a grid with N cells. |
||
| + | |||
| + | ==Library Features== |
||
| + | |||
| + | Functions are provided to generate a list of all cells, a list of neighbors to a particular cell, a list of "triads" to which a cell belongs, and a list of all triads. |
||
| + | |||
| + | A "triad" (my own terminology) is a group of 3 cells that meet at a point. |
||
| + | |||
| + | Another useful function takes a cell ID and returns a vector, which is the center of that cell, as if the whole grid were mapped to a sphere centered at the origin with radius 1. |
||
| + | |||
| + | (I use GlomeVec for my vector library. One could substitute a different library with some minor modifications to the code.) |
||
| + | |||
| + | A function which I have not implemented is the reverse function, which takes any arbitrary point and returns the closest cell. I expect the easiest way to implement such a function efficiently is to sort the cells into a bounding volume hierarchy of some sort, then look up the point (after normalizing it to lie on the surface of the grid) in the BVH to get a small list of candidate cells, and then search the candidate cells for the closest one. |
||
| + | |||
| + | ==Limitations== |
||
| + | |||
| + | The cells aren't quite a uniform size. |
||
| + | |||
| + | The library saves its data in a lazy array indexed by grid size. Sizes larger than 1024 aren't supported. (A maximum-sized grid would then have about 10 million cells.) |
||
| + | |||
| + | ==Links== |
||
| + | |||
| + | * [http://hackage.haskell.org/package/IcoGrid IcoGrid on Hackage] |
||
| + | * [http://hackage.haskell.org/package/GlomeVec GlomeVec vector library on Hackage] |
||
Latest revision as of 03:35, 24 January 2010
IcoGrid (Icosohedron Grid) is a haskell library for generating grids of hexagons and pentagons wrapped around a sphere.
It's easier to show than to describe, so here is a screenshot of an OpenGL application I wrote to render a grid generated by IcoGrid:
Grid Overview
The grid is layed out as twenty triangular hexagon grids fitted together to make an icosahedron. The points where file of these triangular grids meet are pentagons. The size of the grid is length of one of the sides of the triangular grids. Thus a grid of size S will have approximately (S^2)*10 cells.
Most of the library functions require the grid size as the first parameter. Cells are identified by integers from [0..N-1] for a grid with N cells.
Library Features
Functions are provided to generate a list of all cells, a list of neighbors to a particular cell, a list of "triads" to which a cell belongs, and a list of all triads.
A "triad" (my own terminology) is a group of 3 cells that meet at a point.
Another useful function takes a cell ID and returns a vector, which is the center of that cell, as if the whole grid were mapped to a sphere centered at the origin with radius 1.
(I use GlomeVec for my vector library. One could substitute a different library with some minor modifications to the code.)
A function which I have not implemented is the reverse function, which takes any arbitrary point and returns the closest cell. I expect the easiest way to implement such a function efficiently is to sort the cells into a bounding volume hierarchy of some sort, then look up the point (after normalizing it to lie on the surface of the grid) in the BVH to get a small list of candidate cells, and then search the candidate cells for the closest one.
Limitations
The cells aren't quite a uniform size.
The library saves its data in a lazy array indexed by grid size. Sizes larger than 1024 aren't supported. (A maximum-sized grid would then have about 10 million cells.)