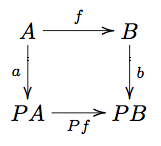Difference between revisions of "User:Michiexile/MATH198/Lecture 9"
Michiexile (talk | contribs) |
Michiexile (talk | contribs) |
||
| Line 1: | Line 1: | ||
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ. |
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ. |
||
| − | |||
| ⚫ | |||
===Recursion patterns=== |
===Recursion patterns=== |
||
| + | |||
| + | ((X, Y and Z)) identified in the paper ((Bananas et.c.)) a number of generic patterns for recursive programming that they had observed, catalogued and systematized. The aim of that paper is to establish a number of ''rules'' for modifying and rewriting expressions involving these generic recursion patterns. |
||
| + | |||
| + | As it turns out, these patterns are instances of the same phenomenon we saw last lecture: where the recursion comes from specifying a different algebra, and then take a uniquely existing morphism induced by initiality (or, as we shall see, finality). |
||
| + | |||
| + | Before we go through the recursion patterns, we need to establish a few pieces of theoretical language, dualizing the Eilenberg-Moore algebra constructions from the last lecture. |
||
| + | |||
| ⚫ | |||
| + | |||
| + | '''Definition''' If <math>P: C\to C</math> is an endofunctor, then a <math>P</math>-''coalgebra'' on <math>A</math> is a morphism <math>a: A\to PA</math>. |
||
| + | |||
| + | A ''morphism of coalgebras'': <math>f: a\to b</math> is some <math>f: A\to B</math> such that the diagram |
||
| + | :[[Image:CoalgebraMorphism.png]] |
||
| + | commutes. |
||
| + | |||
| + | Just as with algebras, we get a category of coalgebras. And the interesting objects here are the ''final coalgebras''. Just as with algebras, we have |
||
| + | |||
| + | '''Lemma''' (''Lambek'') If <math>a: A\to PA</math> is a final coalgebra, it is an isomorphism. |
||
| + | |||
| + | Finally, one thing that makes us care highly about these entities: in an appropriate category (such as <math>\omega-CPO</math>), initial algebras and final coalgebras coincide, with the correspondence given by inverting the algebra/coalgebra morphism. In Haskell not quite true (specifically, the final coalgebra for the lists functor gives us streams...). |
||
| + | |||
| + | Onwards to recursion schemes! |
||
====Catamorphisms==== |
====Catamorphisms==== |
||
| + | |||
| + | A ''catamorphism'' is the uniquely existing morphism from an initial algebra to a different algebra. We have to define maps down to the return value type for each of the constructors of the complex data type we're recursing over, and the catamorphism will deconstruct the structure (trees, lists, ...) and do a generalized ''fold'' over the structure at hand before returning the final value. |
||
| + | |||
| + | The intuition is that for catamorphisms we start essentially structured, and dismantle the structure. |
||
| + | |||
| + | '''Example''': the length function from last lecture. This is the catamorphism for the functor <math>P_A(X) = 1 + A\times X</math> given by the maps |
||
| + | <haskell> |
||
| + | u :: Int |
||
| + | u = 0 |
||
| + | |||
| + | m :: (A, Int) -> Int |
||
| + | m (a, n) = n+1 |
||
| + | </haskell> |
||
====Anamorphisms==== |
====Anamorphisms==== |
||
| + | |||
| + | An ''anamorphism'' is the categorical dual to the catamorphism. It is the canonical morphism from a coalgebra to the final coalgebra for that endofunctor. |
||
| + | |||
| + | Here, we start unstructured, and erect a structure, induced by the coalgebra structures involved. |
||
| + | |||
| + | '''Example''': we can write a recursive function |
||
| + | <haskell> |
||
| + | first :: Int -> [Int] |
||
| + | first 1 = [1] |
||
| + | first n = n : first (n - 1) |
||
| + | </haskell> |
||
| + | This is an anamorphism from the coalgebra for <math>P_{\mathbb N}(X) = 1 + \mathbb N\times X</math> on <math>\mathbb N</math> generated by the two maps |
||
| + | <haskell> |
||
| + | c 0 = Left () |
||
| + | c n = Right (n, n-1) |
||
| + | </haskell> |
||
| + | and we observe that we can chase through the diagram |
||
| + | :[[Image:CoalgebraMorphism.png]] |
||
| + | to conclude that therefore |
||
| + | <haskell> |
||
| + | f 0 = [] |
||
| + | f n = n : f (n - 1) |
||
| + | </haskell> |
||
| + | which is exactly the recursion we wrote to begin with. |
||
====Hylomorphisms==== |
====Hylomorphisms==== |
||
| Line 17: | Line 74: | ||
====Apomorphisms==== |
====Apomorphisms==== |
||
| + | |||
| + | ===Further reading=== |
||
| + | |||
| + | Terminology in the literature: in and out, inl, inr. |
||
| + | |||
| + | |||
| + | ===Homework=== |
||
| + | |||
| + | # Write a fold for the data type <hask>data T a = L a | B a a | C a a a</hask> and demonstrate how this can be written as a catamorphism by giving the algebra it maps to. |
||
| + | # The integers have a partial order induced by the divisibility relation. We can thus take any integer and arrange all its divisors in a tree by having an edge <math>n \to d</math> if <math>d|n</math> and <math>d</math> doesn't divide any other divisor of <math>n</math>. Write an anamorphic function that will generate this tree for a given starting integer. Demonstrate how this function is an anamorphism by giving the algebra it maps from. |
||
Revision as of 08:26, 14 November 2009
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ.
Recursion patterns
((X, Y and Z)) identified in the paper ((Bananas et.c.)) a number of generic patterns for recursive programming that they had observed, catalogued and systematized. The aim of that paper is to establish a number of rules for modifying and rewriting expressions involving these generic recursion patterns.
As it turns out, these patterns are instances of the same phenomenon we saw last lecture: where the recursion comes from specifying a different algebra, and then take a uniquely existing morphism induced by initiality (or, as we shall see, finality).
Before we go through the recursion patterns, we need to establish a few pieces of theoretical language, dualizing the Eilenberg-Moore algebra constructions from the last lecture.
Coalgebras for endofunctors
Definition If is an endofunctor, then a -coalgebra on is a morphism .
A morphism of coalgebras: is some such that the diagram
commutes.
Just as with algebras, we get a category of coalgebras. And the interesting objects here are the final coalgebras. Just as with algebras, we have
Lemma (Lambek) If is a final coalgebra, it is an isomorphism.
Finally, one thing that makes us care highly about these entities: in an appropriate category (such as ), initial algebras and final coalgebras coincide, with the correspondence given by inverting the algebra/coalgebra morphism. In Haskell not quite true (specifically, the final coalgebra for the lists functor gives us streams...).
Onwards to recursion schemes!
Catamorphisms
A catamorphism is the uniquely existing morphism from an initial algebra to a different algebra. We have to define maps down to the return value type for each of the constructors of the complex data type we're recursing over, and the catamorphism will deconstruct the structure (trees, lists, ...) and do a generalized fold over the structure at hand before returning the final value.
The intuition is that for catamorphisms we start essentially structured, and dismantle the structure.
Example: the length function from last lecture. This is the catamorphism for the functor given by the maps
u :: Int
u = 0
m :: (A, Int) -> Int
m (a, n) = n+1
Anamorphisms
An anamorphism is the categorical dual to the catamorphism. It is the canonical morphism from a coalgebra to the final coalgebra for that endofunctor.
Here, we start unstructured, and erect a structure, induced by the coalgebra structures involved.
Example: we can write a recursive function
first :: Int -> [Int]
first 1 = [1]
first n = n : first (n - 1)
This is an anamorphism from the coalgebra for on generated by the two maps
c 0 = Left ()
c n = Right (n, n-1)
and we observe that we can chase through the diagram
to conclude that therefore
f 0 = []
f n = n : f (n - 1)
which is exactly the recursion we wrote to begin with.
Hylomorphisms
Metamorphisms
Paramorphisms
Apomorphisms
Further reading
Terminology in the literature: in and out, inl, inr.
Homework
- Write a fold for the data type
data T a = L a | B a a | C a a aand demonstrate how this can be written as a catamorphism by giving the algebra it maps to. - The integers have a partial order induced by the divisibility relation. We can thus take any integer and arrange all its divisors in a tree by having an edge if and doesn't divide any other divisor of . Write an anamorphic function that will generate this tree for a given starting integer. Demonstrate how this function is an anamorphism by giving the algebra it maps from.