Zipper monad/TravelTree

TravelTree is a library based on the Zipper monad which is used for traversing binary trees. Read the documentation for the Zipper monad if you haven't already.

Definition

data Tree a = Leaf a | Branch (Tree a) (Tree a) deriving (Show, Eq)

data Cxt a = Top
           | L (Cxt  a) (Tree a)
           | R (Tree a) (Cxt  a)
             deriving (Show)

type TreeLoc    a = Loc (Cxt a) (Tree a)
type TravelTree a = Travel (TreeLoc a) (Tree a)

We go with the standard definition of a labelless binary tree. Cxt is for storing the context of an element, and TreeLoc for precisely defining the position of an element within a tree, at the same time as defining the tree itself. See Zipper for an explanation of that idiom.

Functions

Moving around

There are five main functions for stringing together TravelTree computations:

left,  -- moves down a level, through the left branch
right, -- moves down a level, through the right branch
swap,  -- moves from a left branch to a right branch, or vice versa
up,    -- moves to the node's parent
top    -- moves to the top node
:: TravelTree a

All five return the subtree at the new location.

Mutation

The three mutation functions defined by the generic Zipper monad (modifyStruct, getStruct and putStruct) are of course available, but there are no TravelTree-specific mutation functions.

Node classification

There are four functions you can call to find out what kind of node a given location points to:

isTop,   -- is the location the top node?
isChild, -- is the location the child of some other node (i.e. not the top)?
isLeft,  -- is the location a left branch?
isRight  -- is the location a right branch?
:: TreeLoc a -> Bool

Note that these functions are not monadic but instead take a TreeLoc. The TreeLoc pointing to the current node is stored as the state in a TravelTree computation. Thus to call these functions within a do block, use liftM:

do top <- liftM isTop get
   when top $ right >> return ()

Examples

The following examples use as the example tree:

t = Branch (Branch (Branch (Leaf 1) (Leaf 2))
                   (Leaf 3))
           (Branch (Leaf 4)
                   (Leaf 5))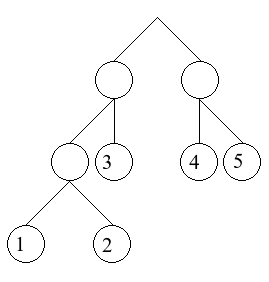

The example tree

A simple path

This is a very simple example showing how to use the movement functions:

leftLeftRight :: TravelTree a
leftLeftRight = do left
                   left
                   right

Result of evaluation:

*Tree> (getTop t) `traverse` leftLeftRight
Leaf 2

Tree reverser

This is a more in-depth example showing getTree and putTree, but is still rather contrived as it's easily done without the zipper (the zipper-less version is shown below).

The algorithm reverses the tree, in the sense that at every branch, the two subtrees are swapped over.

revTree :: Tree a -> Tree a
revTree t = (getTop t) `traverse` revTree' where
    revTree' :: TravelTree a
    revTree' = do t <- getTree
                        case t of
                          Branch _ _ -> do left
                                           l' <- revTree'
                                           swap
                                           r' <- revTree'
                                           up
                                           putTree $ Branch r' l'
                          Leaf x     -> return $ Leaf x

-- without using the zipper:
revTreeZipless :: Tree a -> Tree a
revTreeZipless (Leaf x)       = Leaf x
revTreeZipless (Branch xs ys) = Branch (revTreeZipless ys) (revTreeZipless xs)

Result of evaluation:

*Tree> revTree $ Branch (Leaf 1) (Branch (Branch (Leaf 2) (Leaf 3)) (Leaf 4))
Branch (Branch (Leaf 4) (Branch (Leaf 3) (Leaf 2))) (Leaf 1)

Generalisation

Einar Karttunen (musasabi) suggested generalising this to a recursive tree mapper:

treeMap :: (a -> Tree a)                -- what to put at leaves
        -> (Tree a -> Tree a -> Tree a) -- what to put at branches
        -> (Tree a -> Tree a)           -- combinator function
treeMap leaf branch = \t -> (getTop t) `traverse` treeMap' where
    treeMap' = do t <- getTree
                  case t of
                    Branch _ _ -> do left
                                     l' <- treeMap'
                                     swap
                                     r' <- treeMap'
                                     up
                                     putTree $ branch l' r'
                    Leaf x     -> return $ leaf x

revTree is then easy:

revTreeZipper :: Tree a -> Tree a
revTreeZipper = treeMap Leaf (flip Branch)

It turns out this is a fairly powerful combinator. As with revTree, it can change the structure of a tree. Here's another example which turns a tree into one where siblings are sorted, i.e. given a Branch l r, if l and r are leaves, then the value of l is less than or equal to that of r. Also, if one of l or r is a Branch and the other a Leaf, then l is the Leaf and r the Branch:

sortSiblings :: Ord a => Tree a -> Tree a
sortSiblings = treeMap Leaf minLeaves where
    minLeaves l@(Branch _ _) r@(Leaf _       ) = Branch r l
    minLeaves l@(Leaf _)     r@(Branch _ _   ) = Branch l r
    minLeaves l@(Branch _ _) r@(Branch _ _   ) = Branch l r
    minLeaves l@(Leaf x)     r@(Leaf y       ) = Branch (Leaf $ min x y)
                                                        (Leaf $ max x y)

Result of evaluation:

*Tree> sortSiblings t
Branch (Branch (Leaf 3) (Branch (Leaf 1) (Leaf 2))) (Branch (Leaf 4) (Leaf 5))

Code

The code for the TravelTree library is quite length, so you can just download it. Alternatively, you could download the entire zipper library.