Difference between revisions of "Zipper monad"
DavidHouse (talk | contribs) m (what i described wasn't actually a heap) |
DavidHouse (talk | contribs) m (Leave room for generalisation) |
||
| Line 1: | Line 1: | ||
| − | The TravelTree Monad is a monad proposed and designed by Paolo Martini (xerox), and coded by David House (davidhouse). It is based on the State monad and is used for navigating around |
+ | The TravelTree Monad is a monad proposed and designed by Paolo Martini (xerox), and coded by David House (davidhouse). It is based on the State monad and is used for navigating around data structures, using the concept of [[TheZipper]]. |
| + | |||
| + | As the only zipper currently available is for binary trees, this is what most of the article will be centred around. |
||
== Definition == |
== Definition == |
||
| Line 5: | Line 7: | ||
newtype Travel t a = Travel { unT :: State t a } |
newtype Travel t a = Travel { unT :: State t a } |
||
deriving (Functor, Monad, MonadState t) |
deriving (Functor, Monad, MonadState t) |
||
| − | type TravelTree a = Travel (Loc a) (Tree a) |
+ | type TravelTree a = Travel (Loc a) (Tree a) -- for trees |
</haskell> |
</haskell> |
||
Revision as of 19:44, 17 April 2006
The TravelTree Monad is a monad proposed and designed by Paolo Martini (xerox), and coded by David House (davidhouse). It is based on the State monad and is used for navigating around data structures, using the concept of TheZipper.
As the only zipper currently available is for binary trees, this is what most of the article will be centred around.
Definition
newtype Travel t a = Travel { unT :: State t a }
deriving (Functor, Monad, MonadState t)
type TravelTree a = Travel (Loc a) (Tree a) -- for trees
Computations in TravelTree are stateful. Loc a and Tree a are defined as follows:
data Tree a = Leaf a | Branch (Tree a) (Tree a)
data Cxt a = Top
| L (Cxt a) (Tree a)
| R (Tree a) (Cxt a)
deriving (Show)
type Loc a = (Tree a, Cxt a)
See TheZipper for an explanation of the Cxt and Loc concepts.
Functions
Moving around
There are four main functions for stringing together TravelTree computations:
left, -- moves down a level, through the left branch
right, -- moves down a level, through the right branch
up, -- moves to the node's parent
top -- moves to the top node
:: TravelTree a
All four return the subtree at the new location.
Mutation
There are also functions available for changing the tree:
getTree :: TravelTree a
putTree :: Tree a -> TravelTree a
modifyTree :: (Tree a -> Tree a) -> TravelTree a
These are direct front-doors for State's get, put and modify, and all three return the subtree after any applicable modifications.
Exit points
To get out of the monad, use traverse:
traverse :: Tree a -> TravelTree a -> Tree a
Again, this is just a front-door for evalState, with an initial state of (tt, Top) where tt is the TravelTree passed in.
Examples
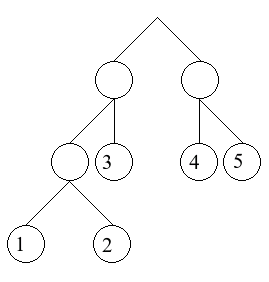
The following examples use as the example tree:
t = Branch (Branch (Branch (Leaf 1) (Leaf 2))
(Leaf 3))
(Branch (Leaf 4)
(Leaf 5))
A simple path
This is a very simple example showing how to use the movement functions:
leftLeftRight :: TravelTree a
leftLeftRight = do left
left
right
Result of evaluation:
*Tree> t `traverse` leftLeftRight Leaf 2
Tree reverser
This is a more in-depth example showing getTree and putTree, but is still rather contrived as it's easily done without the zipper (the zipper-less version is shown below).
The algorithm reverses the tree, in the sense that at every branch, the two subtrees are swapped over.
revTree :: Tree a -> Tree a
revTree t = t `traverse` revTree' where
revTree' :: TravelTree a
revTree' = do t <- getTree
case t of
Branch _ _ -> do left
l' <- revTree'
up
right
r' <- revTree'
up
putTree $ Branch r' l'
Leaf x -> return $ Leaf x
-- without using the zipper:
revTreeZipless :: Tree a -> Tree a
revTreeZipless (Leaf x) = Leaf x
revTreeZipless (Branch xs ys) = Branch (revTreeZipless ys) (revTreeZipless xs)
Result of evaluation:
*Tree> revTree $ Branch (Leaf 1) (Branch (Branch (Leaf 2) (Leaf 3)) (Leaf 4)) Branch (Branch (Leaf 4) (Branch (Leaf 3) (Leaf 2))) (Leaf 1)
Generalisation
Einar Karttunen (musasabi) suggested generalising this to a recursive tree combinator:
treeComb :: (a -> Tree a) -- what to put at leaves
-> (Tree a -> Tree a -> Tree a) -- what to put at branches
-> (Tree a -> Tree a) -- combinator function
treeComb leaf branch = \t -> t `traverse` treeComb' where
treeComb' = do t <- getTree
case t of
Branch _ _ -> do left
l' <- treeComb'
up
right
r' <- treeComb'
up
putTree $ branch l' r'
Leaf x -> return $ leaf x
revTree is then easy:
revTreeZipper :: Tree a -> Tree a
revTreeZipper = treeComb Leaf (flip Branch)
It turns out this is a fairly powerful combinator. As with revTree, it can change the structure of a tree. Here's another example which turns a tree into one where siblings are sorted, i.e. given a Branch l r, if l and r are leaves, then the value of l is less than or equal to that of r. Also, if one of l or r is a Branch and the other a Leaf, then l is the Leaf and r the Branch:
sortSiblings :: Ord a => Tree a -> Tree a
sortSiblings = treeComb Leaf minLeaves where
minLeaves l@(Branch _ _) r@(Leaf _ ) = Branch r l
minLeaves l@(Leaf _) r@(Branch _ _ ) = Branch l r
minLeaves l@(Branch _ _) r@(Branch _ _ ) = Branch l r
minLeaves l@(Leaf x) r@(Leaf y ) = Branch (Leaf $ min x y)
(Leaf $ max x y)
Result of evaluation:
*Tree> sortSiblings t Branch (Branch (Leaf 3) (Branch (Leaf 1) (Leaf 2))) (Branch (Leaf 4) (Leaf 5))
Code
Here's the Zipper Monad in full:
{-# GHC_OPTION -fglasgow-exts #-}
data Cxt a = Top
| L (Cxt a) (Tree a)
| R (Tree a) (Cxt a)
deriving (Show)
type Loc a = (Tree a, Cxt a)
newtype Travel t a = Travel { unT :: State t a }
deriving (Functor, Monad, MonadState t)
type TravelTree a = Travel (Loc a) (Tree a)
left :: TravelTree a
left = modify left' >> liftM fst get where
left' (Branch l r, c) = (l, L c r)
right :: TravelTree a
right = modify right' >> liftM fst get where
right' (Branch l r, c) = (r, R l c)
up :: TravelTree a
up = modify up' >> liftM fst get where
up' (t, L c r) = (Branch t r, c)
up' (t, R l c) = (Branch l t, c)
top :: TravelTree a
top = modify (second $ const Top) >> liftM fst get
modifyTree :: (Tree a -> Tree a) -> TravelTree a
modifyTree f = modify (first f) >> liftM fst get
putTree :: Tree a -> TravelTree a
putTree t = modifyTree $ const t
getTree :: TravelTree a
getTree = modifyTree id -- works because modifyTree returns the 'new' tree
traverse :: Tree a -> TravelTree a -> Tree a
traverse t tt = evalState (unT tt) (t, Top)