Zipper monad

The TravelTree Monad is a monad proposed and designed by Paolo Martini (xerox), and coded by David House (davidhouse). It is based on the State monad and is used for navigating around in binary trees, using the concept of TheZipper.

Definition

newtype Travel t a = Travel { unT :: State t a }
     deriving (Functor, Monad, MonadState t)
type TravelTree a = Travel (Loc a) (Tree a)

Computations in TravelTree</hask> are stateful. Loc a</hask> and Tree a</hask> are defined as follows:

data Tree a = Leaf a | Branch (Tree a) (Tree a)

data Cxt a = Top
           | L (Cxt a) (Tree a)
           | R (Tree a) (Cxt a)
  deriving (Show)

type Loc a = (Tree a, Cxt a)

See TheZipper for an explanation of the Cxt</hask> and Loc</hask> concepts.

Functions

Moving around

There are four main functions for stringing together TravelTree</hask> computations:

left,  -- moves down a level, through the left branch
right, -- moves down a level, through the right branch
up,    -- moves to the node's parent
top    -- moves to the top node
:: TravelTree a

All four return the subtree at the new location.

Mutation

There are also functions available for changing the tree:

getTree    :: TravelTree a
putTree    :: Tree a -> TravelTree a
modifyTree :: (Tree a -> Tree a) -> TravelTree a

These are direct front-doors for State's get, put and modify, and all three return the subtree after any applicable modifications.

Exit points

To get out of the monad, use traverse:

traverse :: Tree a -> TravelTree a -> Tree a

Again, this is just a front-door for evalState, with an initial state of (tt, Top) where tt is the TravelTree passed in.

Examples

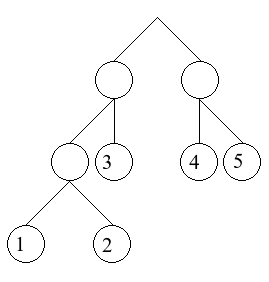
The following examples use as the example tree:

t = Branch (Branch (Branch (Leaf 1) (Leaf 2))
                   (Leaf 3))
           (Branch (Leaf 4)
                   (Leaf 5))

The example tree

Code

data Cxt a = Top
           | L (Cxt a) (Tree a)
           | R (Tree a) (Cxt a)
  deriving (Show)

type Loc a = (Tree a, Cxt a)

newtype Travel t a = Travel { unT :: State t a }
     deriving (Functor, Monad, MonadState t)
type TravelTree a = Travel (Loc a) (Tree a)

t = Branch (Branch (Branch (Leaf 1) (Leaf 2))
                   (Leaf 3))
           (Branch (Leaf 4)
                   (Leaf 5))

left :: TravelTree a
left = modify left' >> liftM fst get where
    left' (Branch l r, c) = (l, L c r)

right :: TravelTree a
right = modify right' >> liftM fst get where
    right' (Branch l r, c) = (r, R l c)

up :: TravelTree a
up = modify up' >> liftM fst get where 
    up' (t, L c r) = (Branch t r, c)
    up' (t, R l c) = (Branch l t, c)

top :: TravelTree a
top = modify (second $ const Top) >> liftM fst get

modifyTree :: (Tree a -> Tree a) -> TravelTree a
modifyTree f = modify (first f) >> liftM fst get

putTree :: Tree a -> TravelTree a
putTree t = modifyTree $ const t

getTree :: TravelTree a
getTree = modifyTree id -- works because modifyTree returns the 'new' tree

traverse :: Tree a -> TravelTree a -> Tree a
traverse t tt = evalState (unT tt) (t, Top)

leftLeftRight :: TravelTree a
leftLeftRight = do left
                   left
                   right

revTreeZipper :: Tree a -> Tree a
revTreeZipper t = t `traverse` revTreeZipper' where
    revTreeZipper' :: TravelTree a
    revTreeZipper' = do t <- getTree
                        case t of
                          Branch _ _ -> do left
                                           l' <- revTreeZipper'
                                           up
                                           right
                                           r' <- revTreeZipper'
                                           up
                                           putTree $ Branch r' l'
                          Leaf x     -> return $ Leaf x