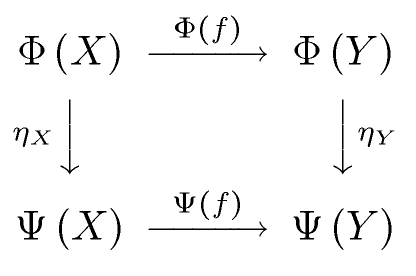Difference between revisions of "Category theory/Natural transformation"
Jump to navigation
Jump to search
Example:
EndreyMark (talk | contribs) (Fix broken link) |
EndreyMark (talk | contribs) (→Commutative diagram: Definition of notion ``natural transformation'') |
||
| Line 15: | Line 15: | ||
=== Commutative diagram === |
=== Commutative diagram === |
||
| − | Let <math>\mathcal C</math>, <math>\mathcal D</math> denote categories. |
+ | * Let <math>\mathcal C</math>, <math>\mathcal D</math> denote categories. |
| − | Let <math>\Phi, \Psi : \mathcal C \to \mathcal D</math> be functors. |
+ | * Let <math>\Phi, \Psi : \mathcal C \to \mathcal D</math> be functors. |
| + | * Let <math>X, Y \in \mathbf{Ob}(\mathcal C)</math>. Let <math>f \in \mathrm{Hom}_{\mathcal C}(X, Y)</math>. |
||
| − | Let us define the <math>\eta : \Phi \to \Psi</math> natural transformation. |
||
| + | Let us define the <math>\eta : \Phi \to \Psi</math> natural transformation. It associates to each object of <math>\mathcal{C}</math> a morphism of <math>\mathcal{D}</math> in the following way (usually, not sets are discussed here, but proper classes, so I do not use term “function” for this <math>\mathbf{Ob}(\mathcal C) \to \mathbf{Mor}(\mathcal D)</math> mapping): |
||
| + | * <math>\forall A \in \mathbf{Ob}(\mathcal C) \longmapsto \eta_A \in \mathrm{Hom}_{\mathcal D}(\Phi(A), \Psi(A))</math>. We call <math>\eta_A</math> the component of <math>\eta</math> at ''A''. |
||
| + | * <math>\eta_Y \cdot \Phi(f) = \Psi(f) \cdot \eta_X</math> |
||
| + | Thus, the following diagram commutes: |
||
| ⚫ | |||
| − | ............ |
||
| − | |||
| ⚫ | |||
=== Vertical arrows: sides of objects === |
=== Vertical arrows: sides of objects === |
||
Revision as of 14:37, 3 October 2006
Example: maybeToList
maybeToList map even $ maybeToList $ Just 5
yields the same as
maybeToList $ fmap even $ Just 5
yields: both yield
[False]
Commutative diagram
- Let , denote categories.
- Let be functors.
- Let . Let .
Let us define the natural transformation. It associates to each object of a morphism of in the following way (usually, not sets are discussed here, but proper classes, so I do not use term “function” for this mapping):
- . We call the component of at A.
Thus, the following diagram commutes:
Vertical arrows: sides of objects
… showing how the natural transformation works.
maybeToList :: Maybe a -> [a]
Left: side of X object
maybeToList :: Maybe Int -> [Int]
| |
Nothing
|
[]
|
Just 0
|
[0]
|
Just 1
|
[1]
|
Right: side of Y object
maybeToList :: Maybe Bool -> [Bool]
| |
Nothing
|
[]
|
Just True
|
[True]
|
Just False
|
[False]
|
Horizontal arrows: sides of functors
even :: Int -> Bool
Side of functor
fmap even:: Maybe Int -> Maybe Bool
| |
Nothing
|
Nothing
|
Just 0
|
Just True
|
Just 1
|
Just False
|
Side of functor
map even:: [Int] -> [Bool]
| |
[]
|
[]
|
[0]
|
[True]
|
[1]
|
[False]
|
Commutativity of the diagram
both paths span between
Maybe Int -> [Bool]
| ||
map even . maybeToList
|
maybeToList . fmap even
| |
Nothing
|
[]
|
[]
|
Just 0
|
[True]
|
[True]
|
Just 1
|
[False]
|
[False]
|
Remarks
evenhas a more general type (Integral a => a -> Bool) than described here- Words “side”, “horizontal”, “vertical”, “left”, “right” serve here only to point to the discussed parts of a diagram, thus, they are not part of the scientific terminology.
- If You want to modifiy the #Commutative diagram, see its source code (in LaTeX using
amscd).
External links
- The corresponding HaWiki article is not migrated here yet, so You can see it for more information.
- Wikipedia's Natural transformation article