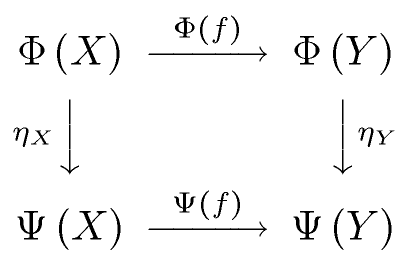Category theory/Natural transformation

Example: maybeToList

 map even $ maybeToList $ Just 5

yields the same as

 maybeToList $ fmap even $ Just 5

yields: both yield

 [False]

In the followings, this example will be used to illustrate the notion of natural transformation.

Definition

• Let ${\mathcal {C}}$, ${\mathcal {D}}$ denote categories.
• Let $\Phi ,\Psi :{\mathcal {C}}\to {\mathcal {D}}$ be functors.
• Let $X,Y\in \mathbf {Ob} ({\mathcal {C}})$. Let $f\in \mathrm {Hom} _{\mathcal {C}}(X,Y)$.

Let us define the $\eta :\Phi \to \Psi$ natural transformation. It associates to each object of ${\mathcal {C}}$ a morphism of ${\mathcal {D}}$ in the following way (usually, not sets are discussed here, but proper classes, so I do not use term “function” for this $\mathbf {Ob} ({\mathcal {C}})\to \mathbf {Mor} ({\mathcal {D}})$ mapping):

• $\forall A\in \mathbf {Ob} ({\mathcal {C}})\longmapsto \eta _{A}\in \mathrm {Hom} _{\mathcal {D}}(\Phi (A),\Psi (A))$. We call $\eta _{A}$ the component of $\eta$ at A.
• $\eta _{Y}\cdot \Phi (f)=\Psi (f)\cdot \eta _{X}$

Thus, the following diagram commutes (in ${\mathcal {D}}$):

Vertical arrows: sides of objects

… showing how the natural transformation works.

$\eta :\Phi \to \Psi$

maybeToList :: Maybe a -> [a]

Left: side of X object

$\eta _{X}:\Phi (X)\to \Psi (X)$

	maybeToList :: Maybe Int -> [Int]
Nothing	[]
Just 0	[0]
Just 1	[1]

Right: side of Y object

$\eta _{Y}:\Phi (Y)\to \Psi (Y)$

	maybeToList :: Maybe Bool -> [Bool]
Nothing	[]
Just True	[True]
Just False	[False]

Horizontal arrows: sides of functors

$f:X\to Y$

 even :: Int -> Bool

Side of $\Phi$ functor

$\Phi (f):\Phi (X)\to \Phi (Y)$

	fmap even:: Maybe Int -> Maybe Bool
Nothing	Nothing
Just 0	Just True
Just 1	Just False

Side of $\Psi$ functor

$\Psi (f):\Psi (X)\to \Psi (Y)$

	map even:: [Int] -> [Bool]
[]	[]
[0]	[True]
[1]	[False]

Commutativity of the diagram

$\Psi (f)\cdot \eta _{X}=\eta _{Y}\cdot \Phi (f)$

both paths span between

$\Phi (X)\to \Psi (Y)$

	Maybe Int -> [Bool]
	map even . maybeToList	maybeToList . fmap even
Nothing	[]	[]
Just 0	[True]	[True]
Just 1	[False]	[False]

Remarks

• even has a more general type (Integral a => a -> Bool) than described here
• Words “side”, “horizontal”, “vertical”, “left”, “right” serve here only to point to the discussed parts of a diagram, thus, they are not part of the scientific terminology.
• If You want to modifiy the commutative diagram, see its source code (in LaTeX using amscd).

Operations

Functor and natural transformation

Let us imagine a parser library, which contains functions for parsing a form. There are two kinds of cells:

• containing data which are optional (e.g. name of spouse)
• containing data which consist of an enumaration of items (e.g. names of acquired languages)

 spouse :: Parser (Maybe String)
 languages :: Parser [String]

Let us imagine we have any processing (storing, archiving etc.) function which processes lists (or any other reason which forces us to convert our results tu list fomrat instead of lists). (Maybe all this example is unparactical and exaggerated!)

We can convert Maybe to list with maybeToList But if we want to do something similar with a parser on Maybe's to achieve a parser on list, then maybeToList is not enough alone, we must fmap it. E.g. if we want to convert a parser like spouse to be of the same type as languages:

 fmap maybeToList spouse

Let us see the types: We start with

 spouse :: Parser (Maybe String)

$\Lambda (\Phi (X))$

or using notion of composing functors

$(\Lambda \Phi )(X)$

We want to achieve

 fmap maybeToList spouse :: Parser [String]

$\Lambda (\Psi (X))$

$(\Lambda \Psi )(X)$

thus we can infer

 fmap maybeToList :: Parser (Maybe [String]) -> Parser [String]

$\mathrm {Hom} {(\Lambda \Phi )(X),\;(\Lambda \Psi )(X)}$

In fact, we have a new “datatype converter”: converting not Maybe's to lists, but parser on Maybe to Parser on list. Let us notate the corresponding natural transformation with $\Lambda \eta$:

To each $X\in \mathbf {Ob} ({\mathcal {C}})$ we associate $(\Lambda \eta )_{X}\in \mathrm {Hom} _{\mathcal {D}}(\Lambda \Phi )(X),\;(\Lambda \Psi )(X))$

$\Lambda \eta :\Lambda \Phi \to \Lambda \Psi$

$(\Lambda \eta )_{X}=\Lambda (\eta _{X})$

Natural transformation and functor

$\eta \Delta :\Phi \Delta \to \Psi \Delta$

$(\eta \Delta )_{X}=\eta _{\Delta (X)}$

It can be illustrated by Haskell examples, too. Understanding it is made harder (easier?) by the fact that Haskell's type inference “dissolves” the main point, thus there is no “materialized” manifestation of it.

External links

• The corresponding HaWiki article is not migrated here yet, so You can see it for more information.
• Wikipedia's Natural transformation article