Difference between revisions of "Fold"
(→Examples: fix link) |
(→Tree-like folds: mention data-ordlist's equivalents) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
==Overview== |
==Overview== |
||
| − | Typically, a fold deals with two things: a combining [[Function|function]], and a [[data structure]], typically a [[List (computing)|list]] of elements. The fold then proceeds to combine elements of the data structure using the function in some systematic way. For instance, we might write |
+ | Typically, a fold deals with two things: a combining [[Function|function]], and a [[data structure]], typically a [[List (computing)|list]] of elements. The fold then proceeds to combine elements of the data structure using the function in some systematic way. For instance, we might want to use a hypothetical function <code>fold</code> to write |
fold (+) [1,2,3,4,5] |
fold (+) [1,2,3,4,5] |
||
| − | which would result in 1 + 2 + 3 + 4 + 5, which is 15. In this instance, + is an [[associative operation]] so how one parenthesizes the addition is irrelevant to what the final result value will be, although the operational details will differ as to ''how'' it will be calculated. To a rough approximation, you can think of the fold as replacing the commas in the list with the + operation. |
+ | which would result in 1 + 2 + 3 + 4 + 5, which is 15. In this instance, + is an [[associative operation]] so how one parenthesizes the addition is irrelevant to what the final result value will be, although the operational details will differ as to ''how'' exactly it will be calculated. To a rough approximation, you can think of the fold as replacing the commas in the list with the + operation. |
However, in the general case, functions of two parameters are not associative, so the order in which one carries out the combination of the elements matters. On lists, there are two obvious ways to carry this out: either by recursively combining the first element with the results of combining the rest (called a ''right fold'') or by recursively combining the results of combining all but the last element with the last one, (called a ''left fold''). Also, in practice, it is convenient and natural to have an initial value which in the case of a right fold, is used when one reaches the end of the list, and in the case of a left fold, is what is initially combined with the first element of the list. This is perhaps clearer to see in the equations defining <code>foldr</code> and <code>foldl</code> in Haskell. Note that in Haskell, <code>[]</code> represents the empty list, and <code>(x:xs)</code> represents the list starting with x and where the rest of the list is xs. |
However, in the general case, functions of two parameters are not associative, so the order in which one carries out the combination of the elements matters. On lists, there are two obvious ways to carry this out: either by recursively combining the first element with the results of combining the rest (called a ''right fold'') or by recursively combining the results of combining all but the last element with the last one, (called a ''left fold''). Also, in practice, it is convenient and natural to have an initial value which in the case of a right fold, is used when one reaches the end of the list, and in the case of a left fold, is what is initially combined with the first element of the list. This is perhaps clearer to see in the equations defining <code>foldr</code> and <code>foldl</code> in Haskell. Note that in Haskell, <code>[]</code> represents the empty list, and <code>(x:xs)</code> represents the list starting with x and where the rest of the list is xs. |
||
| Line 36: | Line 36: | ||
When the function is ''symmetrical'' in its types the parentheses may be placed in arbitrary fashion thus creating a ''tree'' of nested sub-expressions, e.g. ((1 + 2) + (3 + 4)) + 5. If the binary operation is also ''associative'' this value will be well-defined, i.e. same for any parenthesization, although the operational details of ''how'' it is calculated will differ. |
When the function is ''symmetrical'' in its types the parentheses may be placed in arbitrary fashion thus creating a ''tree'' of nested sub-expressions, e.g. ((1 + 2) + (3 + 4)) + 5. If the binary operation is also ''associative'' this value will be well-defined, i.e. same for any parenthesization, although the operational details of ''how'' it is calculated will differ. |
||
| − | Both finite and indefinitely defined lists can be folded over in a tree-like fashion: |
+ | Both finite and indefinitely defined lists can be folded over in a tree-like fashion (except, the <hask>foldt</hask> below, being recursive, can't work with the infinite lists): |
| + | |||
| + | |||
<haskell> |
<haskell> |
||
foldt :: (a -> a -> a) -> a -> [a] -> a |
foldt :: (a -> a -> a) -> a -> [a] -> a |
||
foldt f z [] = z |
foldt f z [] = z |
||
| − | foldt f z [x] = x |
+ | foldt f z [x] = x -- aka foldt' of data-ordlist |
foldt f z xs = foldt f z (pairs f xs) |
foldt f z xs = foldt f z (pairs f xs) |
||
foldi :: (a -> a -> a) -> a -> [a] -> a |
foldi :: (a -> a -> a) -> a -> [a] -> a |
||
foldi f z [] = z |
foldi f z [] = z |
||
| − | foldi f z (x:xs) = f x (foldi f z (pairs f xs)) |
+ | foldi f z (x:xs) = f x (foldi f z (pairs f xs)) -- aka foldt of data-ordlist |
pairs :: (a -> a -> a) -> [a] -> [a] |
pairs :: (a -> a -> a) -> [a] -> [a] |
||
| Line 120: | Line 122: | ||
mergesort xs = foldt merge [] [[x] | x <- xs] |
mergesort xs = foldt merge [] [[x] | x <- xs] |
||
</source> |
</source> |
||
| − | with the function <code>merge</code> a duplicates- |
+ | with the function <code>merge</code> a simpler, duplicates-ignoring variant of <code>union</code>.<br> |
Functions <code>head</code> and <code>last</code> could have been defined through folding as |
Functions <code>head</code> and <code>last</code> could have been defined through folding as |
||
| Line 136: | Line 138: | ||
==External links== |
==External links== |
||
*[http://www.cse.unsw.edu.au/~en1000/haskell/hof.html "Lists, Map, Fold and Tail Recursion"] |
*[http://www.cse.unsw.edu.au/~en1000/haskell/hof.html "Lists, Map, Fold and Tail Recursion"] |
||
| − | *[http://www. |
+ | *[http://www.cantab.net/users/antoni.diller/haskell/units/unit06.html "Unit 6: The Higher-order fold Functions"] |
Latest revision as of 18:51, 28 March 2019
In functional programming, fold (or reduce) is a family of higher order functions that process a data structure in some order and build a return value. This is as opposed to the family of unfold functions which take a starting value and apply it to a function to generate a data structure.
Overview
Typically, a fold deals with two things: a combining function, and a data structure, typically a list of elements. The fold then proceeds to combine elements of the data structure using the function in some systematic way. For instance, we might want to use a hypothetical function fold to write
fold (+) [1,2,3,4,5]
which would result in 1 + 2 + 3 + 4 + 5, which is 15. In this instance, + is an associative operation so how one parenthesizes the addition is irrelevant to what the final result value will be, although the operational details will differ as to how exactly it will be calculated. To a rough approximation, you can think of the fold as replacing the commas in the list with the + operation.
However, in the general case, functions of two parameters are not associative, so the order in which one carries out the combination of the elements matters. On lists, there are two obvious ways to carry this out: either by recursively combining the first element with the results of combining the rest (called a right fold) or by recursively combining the results of combining all but the last element with the last one, (called a left fold). Also, in practice, it is convenient and natural to have an initial value which in the case of a right fold, is used when one reaches the end of the list, and in the case of a left fold, is what is initially combined with the first element of the list. This is perhaps clearer to see in the equations defining foldr and foldl in Haskell. Note that in Haskell, [] represents the empty list, and (x:xs) represents the list starting with x and where the rest of the list is xs.
-- if the list is empty, the result is the initial value z; else
-- apply f to the first element and the result of folding the rest
foldr f z [] = z
foldr f z (x:xs) = f x (foldr f z xs)
-- if the list is empty, the result is the initial value; else
-- we recurse immediately, making the new initial value the result
-- of combining the old initial value with the first element.
foldl f z [] = z
foldl f z (x:xs) = foldl f (f z x) xs
One important thing to note in the presence of lazy, or normal-order evaluation, is that foldr will immediately return the application of f to the recursive case of folding over the rest of the list. Thus, if f is able to produce some part of its result without reference to the recursive case, and the rest of the result is never demanded, then the recursion will stop. This allows right folds to operate on infinite lists. By contrast, foldl will immediately call itself with new parameters until it reaches the end of the list. This tail recursion can be efficiently compiled as a loop, but can't deal with infinite lists at all -- it will recurse forever in an infinite loop. Another technical point to be aware of in the case of left folds in a normal-order evaluation language is that the new initial parameter is not being evaluated before the recursive call is made. This can lead to stack overflows when one reaches the end of the list and tries to evaluate the resulting gigantic expression. For this reason, such languages often provide a stricter variant of left folding which forces the evaluation of the initial parameter before making the recursive call, in Haskell, this is the foldl' (note the apostrophe) function in the Data.List library. Combined with the speed of tail recursion, such folds are very efficient when lazy evaluation of the final result is impossible or undesirable.
Special folds for nonempty lists
One often wants to choose the identity element of the operation f as the initial value z. When no initial value seems appropriate, for example, when one wants to fold the function which computes the maximum of its two parameters over a list in order to get the maximum element of the list, there are variants of foldr and foldl which use the last and first element of the list respectively as the initial value. In Haskell and several other languages, these are called foldr1 and foldl1, the 1 making reference to the automatic provision of an initial element, and the fact that the lists they are applied to must have at least one element.
These folds use type-symmetrical binary operation: the types of both its arguments, and its result, must be the same. Richard Bird in his 2010 book "Pearls of Functional Algorithm Design" (Cambridge University Press 2010, ISBN 978-0-521-51338-8, p. 42) proposes "a general fold function on non-empty lists" foldrn which transforms its last element, by applying an additional argument function to it, into a value of the result type before starting the folding itself, and is thus able to use type-asymmetrical binary operation like the regular foldr to produce a result of type different from the list's elements type.
Tree-like folds
The use of initial value is mandatory when the combining function is asymmetrical in its types, i.e. when the type of its result is different from the type of list's elements. Then an initial value must be used, with the same type as that of the function's result, for a linear chain of applications to be possible, whether left- or right-oriented.
When the function is symmetrical in its types the parentheses may be placed in arbitrary fashion thus creating a tree of nested sub-expressions, e.g. ((1 + 2) + (3 + 4)) + 5. If the binary operation is also associative this value will be well-defined, i.e. same for any parenthesization, although the operational details of how it is calculated will differ.
Both finite and indefinitely defined lists can be folded over in a tree-like fashion (except, the foldt below, being recursive, can't work with the infinite lists):
foldt :: (a -> a -> a) -> a -> [a] -> a
foldt f z [] = z
foldt f z [x] = x -- aka foldt' of data-ordlist
foldt f z xs = foldt f z (pairs f xs)
foldi :: (a -> a -> a) -> a -> [a] -> a
foldi f z [] = z
foldi f z (x:xs) = f x (foldi f z (pairs f xs)) -- aka foldt of data-ordlist
pairs :: (a -> a -> a) -> [a] -> [a]
pairs f (x:y:t) = f x y : pairs f t
pairs f t = t
In the case of foldi function, to avoid its runaway evaluation on indefinitely defined lists the function f must not always demand its second argument's value, at least not all of it, and/or not immediately (example below).
Folds in other languages
In Scheme, right and left fold can be written as:
(define (foldr f z xs)
(if (null? xs)
z
(f (car xs) (foldr f z (cdr xs)))))
(define (foldl f z xs)
(if (null? xs)
z
(foldl f (f z (car xs)) (cdr xs))))
The C++ Standard Template Library implements left fold as the function "accumulate" (in the header <numeric>).
List folds as structural transformations
One way in which it is perhaps natural to view folds is as a mechanism for replacing the structural components of a data structure with other functions and values in some regular way. In many languages, lists are built up from two primitives: either the list is the empty list, commonly called nil, or it is a list constructed by appending an element to the start of some other list, which we call a cons. In Haskell, the cons operation is written as a colon (:), and in scheme and other lisps, it is called cons. One can view a right fold as replacing the nil at the end of the list with a specific value, and each cons with a specific other function. Hence, one gets a diagram which looks something like this:
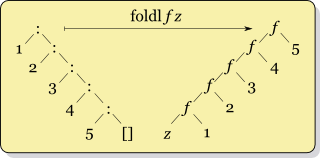
In the case of a left fold, the structural transformation being performed is somewhat less natural, but is still quite regular:
These pictures do a rather nice job of motivating the names left and right fold visually. It also makes obvious the fact that foldr (:) [] is the identity function on lists, as replacing cons with cons and nil with nil will not change anything. The left fold diagram suggests an easy way to reverse a list, foldl (flip (:)) []. Note that the parameters to cons must be flipped, because the element to add is now the right hand parameter of the combining function. Another easy result to see from this vantage-point is to write the higher-order map function in terms of foldr, by composing the function to act on the elements with cons, as:
map f = foldr ((:) . f) []
where the period (.) is an operator denoting function composition.
This way of looking at things provides a simple route to designing fold-like functions on other algebraic data structures, like various sorts of trees. One writes a function which recursively replaces the constructors of the datatype with provided functions, and any constant values of the type with provided values. Such functions are generally referred to as Catamorphisms.
Examples
Using a Haskell interpreter, we can show the structural transformation which fold functions perform by constructing a string as follows:
Prelude> foldr (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(1+(2+(3+(4+(5+(6+(7+(8+(9+(10+(11+(12+(13+0)))))))))))))"
Prelude> foldl (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(((((((((((((0+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)+11)+12)+13)"
Prelude> foldt (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"((((1+2)+(3+4))+((5+6)+(7+8)))+(((9+10)+(11+12))+13))"
Prelude> foldi (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(1+((2+3)+(((4+5)+(6+7))+((((8+9)+(10+11))+(12+13))+0))))"
Infinite tree-like folding is demonstrated e.g. in primes production by unbounded sieve of Eratosthenes:
primes :: (Integral a) => [a]
primes = 2 : 3 : ([5,7..] `minus`
foldi (\(x:xs) -> (x:) . union xs) []
[[p*p, p*p+2*p..] | p <- tail primes])
where the function union operates on ordered lists in a local manner to efficiently produce their union, and minus their set difference, defined at Data.List.Ordered package or here at Prime numbers page.
For finite lists, e.g. merge sort could be easily defined using tree-like folding as
mergesort :: (Ord a) => [a] -> [a]
mergesort xs = foldt merge [] [[x] | x <- xs]
with the function merge a simpler, duplicates-ignoring variant of union.
Functions head and last could have been defined through folding as
head = foldr (\a b->a) undefined
last = foldl (\a b->b) undefined