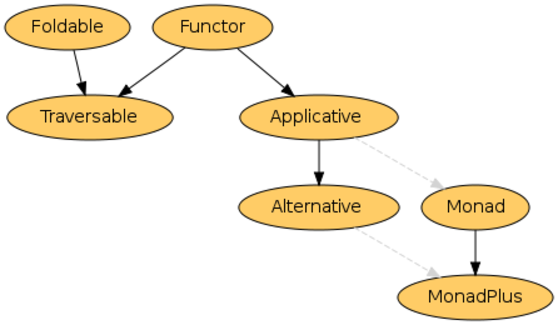
Foldable and Traversable
Data.Sequence is recommended as an efficient alternative to [list]s, with a more symmetric feel and better complexity on various operations.
When you've been using it for a little while, there seem to be some baffling omissions from the API. The first couple you are likely to notice are the absence of "map" and "toList".
The answer to these lies in the long list of instances which Sequence has:
- The Sequence version of map is "
fmap", which comes from the Functor class. - The Sequence version of
toListis in theFoldableclass.
When working with Sequence you also want to refer to the documentation
for at least Foldable and Traversable. Functor only has the single method, so we've already covered that.
What do these classes all mean? A brief tour:
Functor
FunctorA functor is simply a container. Given a container, and a function which works on the elements, we can apply that function to each element. For lists, the familiar "map" does exactly this.
Note that the function can produce elements of a different type, so we may have a different type at the end.
Examples:
Prelude Data.Sequence> map (\n -> replicate n 'a') [1,3,5]
["a","aaa","aaaaa"]
Prelude Data.Sequence> fmap (\n -> replicate n 'a') (1 <| 3 <| 5 <| empty)
fromList ["a","aaa","aaaaa"]
Foldable
A Foldable type is also a container (although the class does not
technically require Functor, interesting Foldables are all Functors). It is a container with the added property that its items can be 'folded' to a summary value. In other words, it is a type which supports "foldr".
Once you support foldr, of course, you can be turned into a list, by using toList = foldr (:) []. This means that all Foldables have a representation as a list, but the order of the items may or may not have any particular significance. However, if a Foldable is also a Functor, parametricity and the Functor law guarantee that toList and fmap commute. Further, in the case of Data.Sequence, there is a well defined order and it is exposed as expected by toList.
A particular kind of fold well-used by Haskell programmers is mapM_, which is a kind of fold over (>>), and Foldable provides this along with the related sequence_.
Traversable
A Traversable type is a kind of upgraded Foldable. Where Foldable
gives you the ability to go through the structure processing the
elements (foldr) but throwing away the shape, Traversable allows you
to do that whilst preserving the shape and, e.g., putting new values
in.
Traversable is what we need for mapM and
sequence : note the apparently surprising fact that the
"_" versions are in a different typeclass.
Some trickier functions: concatMap and filter
Neither Traversable nor Foldable contain elements for concatMap and filter. That is because Foldable is about tearing down the structure
completely, while Traversable is about preserving the structure
exactly as-is. On the other hand concatMap tries to
'squeeze more elements in' at a place and filter tries to
cut them out.
You can write concatMap for Sequence as follows:
concatMap :: (a -> Seq b) -> Seq a -> Seq b
concatMap = foldMap
But why does it work? It works because sequence is an instance of Monoid, where the monoidal operation is "appending". The same
definition works for lists, and we can write it more generally as:
concatMap :: (Foldable f, Monoid (f b)) => (a -> f b) -> f a -> f b
concatMap = foldMap
And that works with lists and sequences both. Does it work with any
Monoid which is Foldable? Only if the Monoid 'means the right
thing'. If you have toList (f `mappend` g) = toList f ++ toList g then it definitely makes sense. In fact this easy to write
condition is stronger than needed; it would be good enough if they
were permutations of each other.
filter turns out to be slightly harder still. You need
something like 'singleton' (from Sequence), or \a -> [a]
for lists. We can use pure from Applicative, although
it's not really right to bring Applicative in for this, and get:
filter :: (Applicative f, Foldable f, Monoid (f a)) =>
(a -> Bool) -> f a -> f a
filter p = foldMap (\a -> if p a then pure a else mempty)
It's interesting to note that, under these conditions, we have a candidate
to help us turn the Foldable into a Monad, since concatMap is a good
definition for >>=, and we can use pure for return.
Generalising zipWith
Another really useful list combinator that doesn't appear in the
interfaces for Sequence, Foldable or Traversable is zipWith. The most general kind of zipWith over Traversables will keep the exact shape of
the Traversable on the left, whilst zipping against the values on the right. It turns out you can get away with a Foldable on the right, but you need to use a Monad (or an Applicative, actually) to thread the
values through:
import Prelude hiding (sequence)
import Data.Sequence
import Data.Foldable
import Data.Traversable
import Control.Applicative
data Supply s v = Supply { unSupply :: [s] -> ([s],v) }
instance Functor (Supply s) where
fmap f av = Supply (\l -> let (l',v) = unSupply av l in (l',f v))
instance Applicative (Supply s) where
pure v = Supply (\l -> (l,v))
af <*> av = Supply (\l -> let (l',f) = unSupply af l
(l'',v) = unSupply av l'
in (l'',f v))
runSupply :: (Supply s v) -> [s] -> v
runSupply av l = snd $ unSupply av l
supply :: Supply s s
supply = Supply (\(x:xs) -> (xs,x))
zipTF :: (Traversable t, Foldable f) => t a -> f b -> t (a,b)
zipTF t f = runSupply (traverse (\a -> (,) a <$> supply) t) (toList f)
zipWithTF :: (Traversable t,Foldable f) => (a -> b -> c) -> t a -> f b -> t c
zipWithTF g t f = runSupply (traverse (\a -> g a <$> supply) t) (toList f)
zipWithTFM :: (Traversable t,Foldable f,Monad m) =>
(a -> b -> m c) -> t a -> f b -> m (t c)
zipWithTFM g t f = sequence (zipWithTF g t f)
zipWithTFA :: (Traversable t,Foldable f,Applicative m) =>
(a -> b -> m c) -> t a -> f b -> m (t c)
zipWithTFA g t f = sequenceA (zipWithTF g t f)
The code above fails with a pattern match error when the Foldable container doesn't have enough input. Here is an alternative version which provides friendlier error reports and makes use of State instead of the self defined Supply monad.
module GenericZip
(zipWithTF,
zipTF,
zipWithTFA,
zipWithTFM) where
import Data.Foldable
import Data.Traversable
import qualified Data.Traversable as T
import Control.Applicative
import Control.Monad.State
-- | The state contains the list of values obtained form the foldable container
-- and a String indicating the name of the function currectly being executed
data ZipState a = ZipState {fName :: String,
list :: [a]}
-- | State monad containing ZipState
type ZipM l a = State (ZipState l) a
-- | pops the first element of the list inside the state
pop :: ZipM l l
pop = do
st <- get
let xs = list st
n = fName st
case xs of
(a:as) -> do put st{list=as}
return a
[] -> error $ n ++ ": insufficient input"
-- | pop a value form the state and supply it to the second
-- argument of a binary function
supplySecond :: (a -> b -> c) -> a -> ZipM b c
supplySecond f a = do b <- pop
return $ f a b
zipWithTFError :: (Traversable t,Foldable f) =>
String -> (a -> b -> c) -> t a -> f b -> t c
zipWithTFError str g t f = evalState (T.mapM (supplySecond g) t)
(ZipState str (toList f))
zipWithTF :: (Traversable t,Foldable f) => (a -> b -> c) -> t a -> f b -> t c
zipWithTF = zipWithTFError "GenericZip.zipWithTF"
zipTF :: (Traversable t, Foldable f) => t a -> f b -> t (a,b)
zipTF = zipWithTFError "GenericZip.zipTF" (,)
zipWithTFM :: (Traversable t,Foldable f,Monad m) =>
(a -> b -> m c) -> t a -> f b -> m (t c)
zipWithTFM g t f = T.sequence (zipWithTFError "GenericZip.zipWithTFM" g t f)
zipWithTFA :: (Traversable t,Foldable f,Applicative m) =>
(a -> b -> m c) -> t a -> f b -> m (t c)
zipWithTFA g t f = sequenceA (zipWithTFError "GenericZip.zipWithTFA" g t f)
Recent versions of Data.Traversable include generalizations of mapAccumL and mapAccumR from lists to Traversables (encapsulating the state monad used above):
mapAccumL :: Traversable t => (a -> b -> (a, c)) -> a -> t b -> (a, t c)
mapAccumR :: Traversable t => (a -> b -> (a, c)) -> a -> t b -> (a, t c)
Using these, the first version above can be written as
zipWithTF :: (Traversable t, Foldable f) => (a -> b -> c) -> t a -> f b -> t c
zipWithTF g t f = snd (mapAccumL map_one (toList f) t)
where map_one (x:xs) y = (xs, g y x)
Replace mapAccumL with mapAccumR and the elements of the Foldable are zipped in reverse order.
Similarly, we can define a generalization of reverse on Traversables, which preserves the shape but reverses the left-to-right position of the elements:
reverseT :: (Traversable t) => t a -> t a
reverseT t = snd (mapAccumR (\ (x:xs) _ -> (xs, x)) (toList t) t)