Difference between revisions of "GPipe"
m |
m |
||
| Line 1: | Line 1: | ||
== What is GPipe? == |
== What is GPipe? == |
||
| − | [http://hackage.haskell.org/package/GPipe GPipe] is a library for programming the GPU (graphics processing unit). It is an alternative to using OpenGl, and has the advantage that it is purely functional, statically typed and operates on immutable data as opposed to OpenGl's inherently imperative style. Another important difference with OpenGl is that with GPipe you don't need to write shaders in a second shader language such as GLSL or Cg, but instead |
+ | [http://hackage.haskell.org/package/GPipe GPipe] is a library for programming the GPU (graphics processing unit). It is an alternative to using OpenGl, and has the advantage that it is purely functional, statically typed and operates on immutable data as opposed to OpenGl's inherently imperative style. Another important difference with OpenGl is that with GPipe you don't need to write shaders in a second shader language such as GLSL or Cg, but instead use regular Haskell functions on the GPU data types. GPipe uses the same conceptual model as OpenGl, and it is recommended that you have at least a basic understanding of how OpenGl works to be able to use GPipe. |
In GPipe, you'll primary work with these four types of data on the GPU: |
In GPipe, you'll primary work with these four types of data on the GPU: |
||
| Line 88: | Line 88: | ||
</haskell> |
</haskell> |
||
| − | Every side of the box is created from a |
+ | Every side of the box is created from a regular list of four elements each, where each element is a tuple with three vectors: a position, a normal and an uv-coordinate. These lists of vertices are then turned into [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Primitive.html#t:PrimitiveStream <hask>PrimitiveStream</hask>]s on the GPU by [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Primitive.html#v:toGPUStream <hask>toGPUStream</hask>] that in our case creates triangle strips from the vertices, i.e 2 triangles from 4 vertices. Refer to the OpenGl specification on how triangle strips and the other topologies works. |
All six sides are then concatenated together into a cube. We can see that the type of the cube is a <hask>PrimitiveStream</hask> of [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Primitive.html#t:Triangle <hask>Triangle</hask>]s where each vertex is a tuple of three vectors, just as the lists we started with. One big difference is that those vectors now are made up of <hask>Vertex Float</hask>s instead of <hask>Float</hask>s since they are now on the GPU. |
All six sides are then concatenated together into a cube. We can see that the type of the cube is a <hask>PrimitiveStream</hask> of [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Primitive.html#t:Triangle <hask>Triangle</hask>]s where each vertex is a tuple of three vectors, just as the lists we started with. One big difference is that those vectors now are made up of <hask>Vertex Float</hask>s instead of <hask>Float</hask>s since they are now on the GPU. |
||
| Line 115: | Line 115: | ||
== FragmentStreams == |
== FragmentStreams == |
||
| − | To render the primitives on the screen, we must first turn them into pixel fragments. This called rasterization and in our example done by the function [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Fragment.html#v:rasterizeFront <hask>rasterizeFront</hask>], which transforms <hask>PrimitiveStream</hask>s into [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Fragment.html#t:FragmentStream <hask>FragmentStream</hask>]s. |
+ | To render the primitives on the screen, we must first turn them into pixel fragments. This is called rasterization and in our example done by the function [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Fragment.html#v:rasterizeFront <hask>rasterizeFront</hask>], which transforms <hask>PrimitiveStream</hask>s into [http://hackage.haskell.org/packages/archive/GPipe/latest/doc/html/Graphics-GPipe-Stream-Fragment.html#t:FragmentStream <hask>FragmentStream</hask>]s. |
<haskell> |
<haskell> |
||
Revision as of 11:54, 12 January 2010
What is GPipe?
GPipe is a library for programming the GPU (graphics processing unit). It is an alternative to using OpenGl, and has the advantage that it is purely functional, statically typed and operates on immutable data as opposed to OpenGl's inherently imperative style. Another important difference with OpenGl is that with GPipe you don't need to write shaders in a second shader language such as GLSL or Cg, but instead use regular Haskell functions on the GPU data types. GPipe uses the same conceptual model as OpenGl, and it is recommended that you have at least a basic understanding of how OpenGl works to be able to use GPipe.
In GPipe, you'll primary work with these four types of data on the GPU:
Let's walk our way through an simple example as I explain how you work with these types. This page is formatted as a literate Haskell page, simply save it as "box.lhs" and then type
ghc --make –O box.lhs box
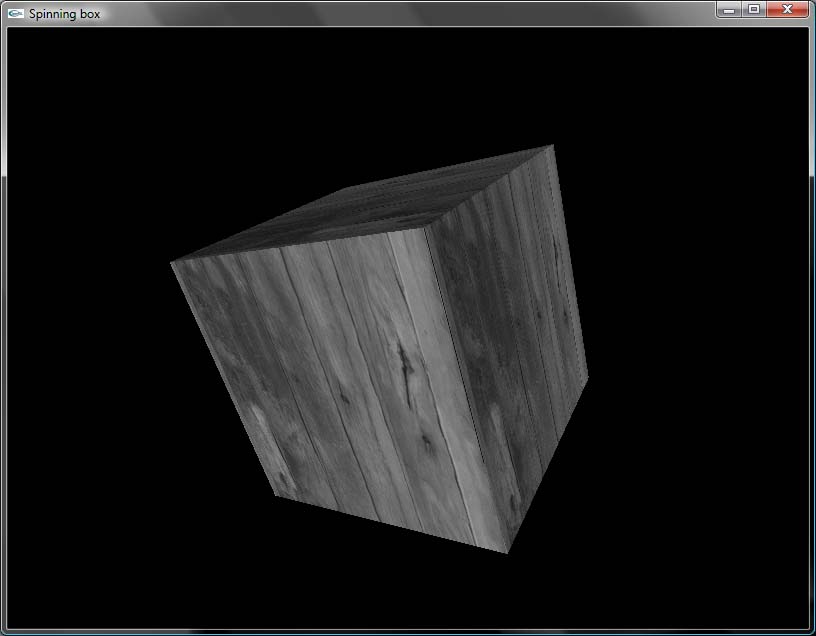
at the prompt to see a spinning box. You’ll also need an image named "myPicture.jpg" in the same directory (I used a picture of some wooden planks).
> module Main where
> import Graphics.GPipe
> import Graphics.GPipe.Texture.Load
> import qualified Data.Vec as Vec
> import Data.Vec.Nat
> import Data.Vec.LinAlg.Transform3D
> import Data.Monoid
> import Data.IORef
> import Graphics.UI.GLUT
> (Window,
> mainLoop,
> postRedisplay,
> idleCallback,
> getArgsAndInitialize,
> ($=))
Besides GPipe, this example also uses the Vec-Transform package for the transformation matrices, and the GPipe-TextureLoad package for loading textures from disc. GLUT is used in GPipe for window management and the main loop.
Creating a window
We start by defining the main function.
> main :: IO ()
> main = do
> getArgsAndInitialize
> tex <- loadTexture RGB8 "myPicture.jpg"
> angleRef <- newIORef 0.0
> newWindow "Spinning box" (100:.100:.()) (800:.600:.()) (renderFrame tex angleRef) initWindow
> mainLoop
> renderFrame :: Texture2D RGBFormat -> IORef Float -> IO (FrameBuffer RGBFormat () ())
> renderFrame tex angleRef = do
> angle <- readIORef angleRef
> writeIORef angleRef ((angle + 0.01) `mod'` (2*pi))
> return $ cubeFrameBuffer tex angle
> initWindow :: Window -> IO ()
> initWindow win = idleCallback $= Just (postRedisplay (Just win))
First we set up GLUT, and load a texture from disc via the GPipe-TextureLoad package function loadTexture. In this example we're going to animate a spinning box, and for that we put an angle in an IORef so that we can update it between frames. We then create a window with newWindowinitWindow registers this window as being continously redisplayed in the idle loop. At each frame, the IO action renderFrame tex angleRef is run. In this function the angle is incremented with 0.01 (reseted each lap), and a FrameBuffer is created and returned to be displayed in the window. But before I explain FrameBuffers, let's jump to the start of the graphics pipeline instead.
PrimitiveStreams
The graphics pipeline starts with creating primitives such as triangles on the GPU.Let's create a box with six sides, each made up of two triangles each.
> cube :: PrimitiveStream Triangle (Vec3 (Vertex Float), Vec3 (Vertex Float), Vec2 (Vertex Float))
> cube = mconcat [sidePosX, sideNegX, sidePosY, sideNegY, sidePosZ, sideNegZ]
> sidePosX = toGPUStream TriangleStrip $ zip3 [1:.0:.0:.(), 1:.1:.0:.(), 1:.0:.1:.(), 1:.1:.1:.()] (repeat (1:.0:.0:.())) uvCoords
> sideNegX = toGPUStream TriangleStrip $ zip3 [0:.0:.1:.(), 0:.1:.1:.(), 0:.0:.0:.(), 0:.1:.0:.()] (repeat ((-1):.0:.0:.())) uvCoords
> sidePosY = toGPUStream TriangleStrip $ zip3 [0:.1:.1:.(), 1:.1:.1:.(), 0:.1:.0:.(), 1:.1:.0:.()] (repeat (0:.1:.0:.())) uvCoords
> sideNegY = toGPUStream TriangleStrip $ zip3 [0:.0:.0:.(), 1:.0:.0:.(), 0:.0:.1:.(), 1:.0:.1:.()] (repeat (0:.(-1):.0:.())) uvCoords
> sidePosZ = toGPUStream TriangleStrip $ zip3 [1:.0:.1:.(), 1:.1:.1:.(), 0:.0:.1:.(), 0:.1:.1:.()] (repeat (0:.0:.1:.())) uvCoords
> sideNegZ = toGPUStream TriangleStrip $ zip3 [0:.0:.0:.(), 0:.1:.0:.(), 1:.0:.0:.(), 1:.1:.0:.()] (repeat (0:.0:.(-1):.())) uvCoords
> uvCoords = [0:.0:.(), 0:.1:.(), 1:.0:.(), 1:.1:.()]
Every side of the box is created from a regular list of four elements each, where each element is a tuple with three vectors: a position, a normal and an uv-coordinate. These lists of vertices are then turned into PrimitiveStreamtoGPUStream
All six sides are then concatenated together into a cube. We can see that the type of the cube is a PrimitiveStream of TriangleVertex Floats instead of Floats since they are now on the GPU.
The cube is defined in model-space, i.e where positions and normals are relative the cube. We now want to rotate that cube using a variable angle and project the whole thing with a perspective projection, as it is seen through a camera 2 units down the z-axis.
> transformedCube :: Float -> PrimitiveStream Triangle (Vec4 (Vertex Float), (Vec3 (Vertex Float), Vec2 (Vertex Float)))
> transformedCube angle = fmap (transform angle) cube
> transform angle (pos, norm, uv) = (transformedPos, (transformedNorm, uv))
> where
> modelMat = rotationVec (normalize (1:.0.5:.0.3:.())) angle `multmm` translation (-0.5)
> viewMat = translation (-(0:.0:.2:.()))
> projMat = perspective 1 100 (pi/3) (4/3)
> viewProjMat = projMat `multmm` viewMat
> transformedPos = toGPU (viewProjMat `multmm` modelMat) `multmv` homPoint pos
> transformedNorm = toGPU (Vec.map (Vec.take n3) $ Vec.take n3 $ modelMat) `multmv` norm
When applying a function on the PrimitiveStream using fmap, that function will be executed on the GPU using vertex shaders. The toGPUFloats into GPU-values like Vertex Float so it can be used with the vertices of the PrimitiveStream.
FragmentStreams
To render the primitives on the screen, we must first turn them into pixel fragments. This is called rasterization and in our example done by the function rasterizeFrontPrimitiveStreams into FragmentStream
> rasterizedCube :: Float -> FragmentStream (Vec3 (Fragment Float), Vec2 (Fragment Float))
> rasterizedCube angle = rasterizeFront $ transformedCube angle
In the rasterization process, values of type Vertex Float are turned into values of type Fragment Float.
For each fragment, we now want to give it a color from the texture we initially loaded, as well as light it with a directional light coming from the camera.
> litCube :: Texture2D RGBFormat -> Float -> FragmentStream (Color RGBFormat (Fragment Float))
> litCube tex angle = fmap (enlight tex) $ rasterizedCube angle
> enlight tex (norm, uv) = RGB (c * Vec.vec (norm `dot` toGPU (0:.0:.1:.())))
> where RGB c = sample (Sampler Linear Wrap) tex uv
Using fmap on a FragmentStream will execute a function on the GPU using fragment shaders. The function sample
Once we have a FragmentStream of Colors, we can paint those fragments onto a FrameBuffer.
FrameBuffers
A FrameBufferFragmentStreams are painted. A FrameBuffer may contain any combination of a color buffer, a depth buffer and a stencil buffer. Besides being shown in windows, FrameBuffers may also be saved to memory or converted to textures, thus enabling multi pass rendering. A FrameBuffer has no defined size, but take the size of the window when shown, or are given a size when saved to memory or converted to a texture.
And so finally, we paint the fragments we have created onto a black FrameBuffer. By this we use paintColor
> cubeFrameBuffer :: Texture2D RGBFormat -> Float -> FrameBuffer RGBFormat () ()
> cubeFrameBuffer tex angle = paintSolid (litCube tex angle) emptyFrameBuffer
> paintSolid = paintColor NoBlending (RGB $ Vec.vec True)
> emptyFrameBuffer = newFrameBufferColor (RGB 0)
This FrameBuffer is the one we return from the renderFrame action we defined at the top.
Screenshot
Questions and feedback
If you have any questions or suggestions, feel free to mail me. I'm also interested in seeing some use cases from the community, as complex or trivial they may be.