Difference between revisions of "Graham Scan Implementation"
Jump to navigation
Jump to search
(add example where this code doesn't work) |
m (→Testing: add graph of points) |
||
| Line 108: | Line 108: | ||
> let f = [(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828),(-34.288098030422404,80.6230134460068),(-6.446932942713564,-11.632835144720378),(2.861905401095031,1.1159493836896193)] |
> let f = [(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828),(-34.288098030422404,80.6230134460068),(-6.446932942713564,-11.632835144720378),(2.861905401095031,1.1159493836896193)] |
||
| − | > gscan f |
+ | > gscan' f |
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828)] |
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828)] |
||
| − | > gscan (gscan f) |
+ | > gscan' (gscan' f) |
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(65.72912810263666,5.955962930412828)] |
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(65.72912810263666,5.955962930412828)] |
||
| − | > gscan (gscan (gscan f)) |
+ | > gscan' (gscan' (gscan' f)) |
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(65.72912810263666,5.955962930412828)] |
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(65.72912810263666,5.955962930412828)] |
||
</haskell> |
</haskell> |
||
| + | |||
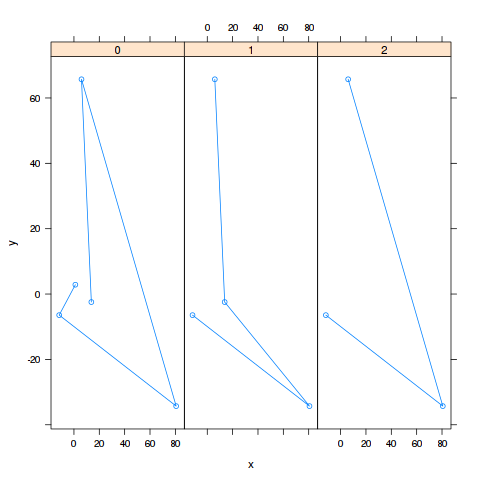
| + | The versions of <tt>f</tt> with differing numbers of gscan applied are: |
||
| + | [[File:Graham_scan_implementation_failure.png]] |
||
Revision as of 03:07, 25 July 2013
Descriptions of this problem can be found in Real World Haskell, Chapter 3
import Data.Ord (comparing)
import Data.List (sortBy)
--Graham Scan exercise
--Direction type
data Direction = LeftTurn
| RightTurn
| Straight
deriving (Show, Eq)
--Point type
data Point = Point (Double, Double)
deriving (Show)
--some points
p0 = Point (2.1,2.0)
p1 = Point (4.2,2.0)
p2 = Point (0.5,2.5)
p3 = Point (3.2,3.5)
p4 = Point (1.2,4.0)
p5 = Point (0.7,4.7)
p6 = Point (1.0,1.0)
p7 = Point (3.0,5.2)
p8 = Point (4.0,4.0)
p9 = Point (3.5,1.5)
pA = Point (0.5,1.0)
points = [p0,p1,p2,p3,p4,p5,p6,p7,p8,p9,pA]
-- Actually, I'd leave it as EQ, GT, LT. Then, actually,
-- if you wanted to sort points rotationally around a single point,
-- sortBy (dir x) would actually work. --wasserman.louis@gmail.com
--Get direction of single set of line segments
dir :: Point -> Point -> Point -> Direction
dir (Point (ax, ay)) (Point (bx, by)) (Point (cx, cy)) = case sign of
EQ -> Straight
GT -> LeftTurn
LT -> RightTurn
where sign = compare ((bx - ax) * (cy - ay)) ((by - ay) * (cx - ax))
--Get a list of Directions from a list of Points
dirlist :: [Point] -> [Direction]
dirlist (x:y:z:xs) = dir x y z : dirlist (y:z:xs)
dirlist _ = []
--Compare Y axes
sortByY :: [Point] -> [Point]
sortByY xs = sortBy lowestY xs
where lowestY (Point(x1,y1)) (Point (x2,y2)) = compare (y1,x1) (y2,x2)
--get COT of line defined by two points and the x-axis
pointAngle :: Point -> Point -> Double
pointAngle (Point (x1, y1)) (Point (x2, y2)) = (x2 - x1) / (y2 - y1)
--compare based on point angle
pointOrdering :: Point -> Point -> Ordering
pointOrdering a b = compare (pointAngle a b) 0.0
--Sort by angle
sortByAngle :: [Point] -> [Point]
sortByAngle ps = bottomLeft : sortBy (compareAngles bottomLeft) (tail (sortedPs))
where sortedPs = sortByY ps
bottomLeft = head (sortedPs)
--Compare angles
compareAngles :: Point -> Point -> Point -> Ordering
compareAngles = comparing . pointAngle
--Graham Scan
gscan :: [Point] -> [Point]
gscan ps = scan (sortByAngle ps)
where scan (x:y:z:xs) = if dir x y z == LeftTurn
then scan (x:z:xs)
else x: scan (y:z:xs)
scan [x,y] = [x,y] -- there's no shame in a pattern match
-- of this type!
scan _ = []
Testing
The above implementation has an error, which can be found using
import Test.QuickCheck
import Control.Monad
import Data.List
gscan' = map (\(Point x) -> x) . gscan . map Point
prop_gscan n = forAll (replicateM n arbitrary) (\xs -> sort (gscan' xs) == sort (gscan' (gscan' xs)))
This leads to a counterexample for lists of 5 elements
> quickCheck (prop_gscan 3)
+++ OK, passed 100 tests.
> quickCheck (prop_gscan 4)
+++ OK, passed 100 tests.
> quickCheck (prop_gscan 5)
*** Failed! Falsifiable (after 10 tests):
[(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828),(-34.288098030422404,80.6230134460068),(-6.446932942713564,-11.632835144720378),(2.861905401095031,1.1159493836896193)]
> let f = [(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828),(-34.288098030422404,80.6230134460068),(-6.446932942713564,-11.632835144720378),(2.861905401095031,1.1159493836896193)]
> gscan' f
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(-2.4444173639942894,13.729627457461254),(65.72912810263666,5.955962930412828)]
> gscan' (gscan' f)
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(65.72912810263666,5.955962930412828)]
> gscan' (gscan' (gscan' f))
[(-6.446932942713564,-11.632835144720378),(-34.288098030422404,80.6230134460068),(65.72912810263666,5.955962930412828)]
The versions of f with differing numbers of gscan applied are: