Difference between revisions of "LGtk/ADT lenses"
m (emphasise question) |
m (→ADT lenses) |
||
| Line 59: | Line 59: | ||
The proposed solution, summarized: |
The proposed solution, summarized: |
||
| − | '''As a lens toolbox for an ADT, use a lens whose ''co''domain is the ADT and whose domain is tuple of the constructor tag and the ADT components.''' |
+ | '''As a lens toolbox for an ADT, use a lens whose ''co''domain is the ADT and whose domain is a tuple of the constructor tag and the ADT components.''' |
Let's see specific examples before the generic descripton of the proposed lens. |
Let's see specific examples before the generic descripton of the proposed lens. |
||
Revision as of 22:54, 7 June 2013
Problem description
Lenses provide uniform and compositional way to view and edit data structures.
For example, one can view and edit pairs with fstLens and sndLens. These two lenses form a toolbox for editing pairs in the sense that given pairs p :: (a, b) and q :: (a, b), by succesive get and set operations p can be changed to be equivalent to q:
q == setL fstLens (getL fstLens q) (setL sndLens (getL sndLens q) p)
Similarly, there is a toolbox of lenses for records which toolbox contains one lens for each record field.
Question:
Are there a toolbox of lenses for algebraic data types with multiple constructors?
Existing solutions
Partial lenses
The data-lens library provides partial lenses which are isomorphic to
type PartialLens a b = (a -> Maybe b, a -> Maybe (b -> a))
The flollowing partial lenses are defined for lists:
headLens :: PartialLens [a] a
headLens = (get, set)
where
get [] = Nothing
get (h:t) = Just h
set [] = Nothing
set (h:t) = Just (:t)
tailLens :: PartialLens [a] [a]
tailLens = (get, set)
where
get [] = Nothing
get (h:t) = Just t
set [] = Nothing
set (h:t) = Just (h:)
Unfortunately headLens and tailLens does not provide a complete toolbox, one cannot change an empty list to a non-empty list with them, for example.
Other solutions
Please help to extend the list of known solutions.
ADT lenses
The proposed solution, summarized:
As a lens toolbox for an ADT, use a lens whose codomain is the ADT and whose domain is a tuple of the constructor tag and the ADT components.
Let's see specific examples before the generic descripton of the proposed lens.
Example: List lens
The lens for lists which forms a complete toolbox:
import Data.Lens.Common
listLens :: Lens (Bool, (a, [a])) [a]
listLens = lens get set where
get (False, _) = []
get (True, (l, r)) = l: r
set [] (_, x) = (False, x)
set (l: r) _ = (True, (l, r))
Here Bool is used as the constructor tag, and a and [a] are the components of the list (head and tail). Intead of a triple we use two pairs, so we reach the parts with fstLens and sndLens.
List lens usage
Suppose that we have a state s of type
type S = (Bool, (Int, [Int]))
We can view and edit the list through the following lenses:
listLens :: Lens S [Int]edits the complete list.fstLens :: Lens S Booledits the top level constructor of the list:Falsecorresponds to[]andTruecorresponds to(:).headLens = fstLens . sndLens :: Lens S Intedits the head of the list.tailLens = sndLens . sndLens :: Lens S [Int]edits the tail of the list.
Remarks:
- If the top level constructor of the list is
[], the head and the tail of the list can still be edited; the change will only be visible throughlistLenswhen the constructor is changed back to(:). This may seem to be odd, but for many applications this is the right behaviour. - For editing the tail of the tail of the list, we need an
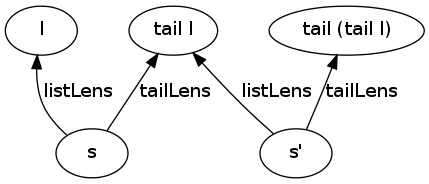
s' :: Ssuch thatsviewed throughtailLensis the same ass'viewed throughlistLens. Explained on a figure:
On the figure, edges are lenses and nodes are references. One possible definition of references is described in LGtk/Semantics#References. How s' can be created and how s and s' can be kept in sync is a related but separate question. LGtk/Semantics#Dependent_reference_creation describes a possible solution.
Example: ADT with repeated record fields
Consider the following ADT:
data X a
= X1 { y :: Int, z :: a }
| X2 { y :: Int, v :: Char }
Note that the y field is defined twice.
For the ADT lens, first define an auxiliary enum type for the constructor tags:
data XTag = X1Tag | X2Tag
The definition of XTag is kind of inevitable if we would like to edit the constructor tags. We could use Bool, but that would not scale to more constructors. We could use Int too, but with less static checks from the type system.
The definition of the lens toolbox for X:
xLens :: Lens (XTag, (Int, (a, Char))) (X a)
xLens = lens get set where
get (X1Tag, (y, (z, _))) = X1 y z
get (X2Tag, (y, (_, v))) = X2 y v
set (X1 y z) (_, (_, (_, v))) = (X1Tag, (y, (z, v)))
set (X2 y v) (_, (_, (z, _))) = (X2Tag, (y, (z, v)))
Remarks:
- Instead of
(XTag, (Int, (a, Char))), we could use(XTag, (Int, a, Char))or(XTag, Int, a, Char)too. This is an implementation detail. xLensremembers the value ofyif we change between the constructor tags. This is the intended behaviour.xLensremembers the values ofvandzfields if we change between the constructor tags. This is the intended behaviour.
Interpreation
The intended behaviour can be justified if we interpret lenses as abstract editors. If we would like to define an editor of an X value, the state of the editor would be (XTag, (Int, (a, Char))), and one could retrive the actual X value by xLens from the state. The editor would be the composition of the following simpler editors:
- An elementary editor for
XTag(maybe a combo box or a checkbox) which would be connected to the editor state byfstLens. - An elementary editor for an
Int(maybe a text box or a slider) which would be connected to the editor state byfstLens . sndLens. - An editor for an
atyped value which would be connected to the editor state byfstLens . sndLens . sndLens. - An editor for a
Char(maybe a combo box or a text box or a virtual keyboard) which would be connected to the editor state byfstLens . sndLens . sndLens . sndLens.
Now, the intended behaviour is the following:
- If the user fills in an
Intvalue fory, this value should remain the same after changing theXTagvalue. - The
avalue editor should be active only if theXTagvalue isX1Tag. - The
Chareditor should be active only if theXTagvalue isX2Tag. - If the user fills in an
avalue forzwhen theXTagvalue isX1Tag, and the user changesX1TagtoX2Tagand then back toX1Tag, theavalue should be the same as before (consider a complex value which is hard to re-create). Similar holds for theCharvalue.
Generic ADT lens
In the generic case, consider the following ADT:
data X a1 ... aN
= X1 { x11 :: t11, x12 :: t12, ... }
| X2 { x21 :: t21, x22 :: t22, ... }
...
| XM { xM1 :: tM1, xM2 :: tM2, ... }
Suppose that the set of different field names are f1 :: s1, f2 :: s2, ..., fK :: sK.
Let cij equal to k iff xij is equal to fk.
Define an auxiliary enum type for the constructor tags:
data XTag = X1Tag | X2Tag | ... | XMTag
The definition of the lens toolbox for X:
xLens :: Lens (XTag, (s1, (s2, ...))) (X a1 ... aN)
xLens = lens get set where
get (X1Tag, (s1, (s2, ...))) = X1 s{c11} s{c12} ...
...
get (XMTag, (s1, (s2, ...))) = X2 s{cM1} s{cM2} ...
-- replace second occurrence of the same variable name by _ in pattern
set (X1 s{c11} s{c12} ...) (_, (s1, (s2, ...))) = (X1Tag, (s1, (s2, ...)))
...
set (XM s{cM1} s{cM2} ...) (_, (s1, (s2, ...))) = (XMTag, (s1, (s2, ...)))
Links and references
I have not seen this technique described before. Please help to extend the list of papers / blog entries, where this or similar technique is used.
[Reddit comments]