Numeric Haskell: A Repa Tutorial
Repa is a Haskell library for high performance, regular, multi-dimensional parallel arrays. All numeric data is stored unboxed and functions written with the Repa combinators are automatically parallel (provided you supply "+RTS -N" on the command line when running the program).
This document provides a tutorial on array programming in Haskell using the repa package.
Note: a companion tutorial to this is provided as the vector tutorial, and is based on the NumPy tutorial.
Authors: Don Stewart.
Quick Tour
Repa (REgular PArallel arrays) is an advanced, multi-dimensional parallel arrays library for Haskell, with a number of distinct capabilities:
- The arrays are "regular" (i.e. dense, rectangular and store elements all of the same type); and
- Functions may be written that are polymorphic in the shape of the array;
- Many operations on arrays are accomplished by changing only the shape of the array (without copying elements);
- The library will automatically parallelize operations over arrays.
This is a quick start guide for the package. For further information, consult:
- The Haddock Documentation
- Regular, Shape-polymorphic, Parallel Arrays in Haskell.
- Efficient Parallel Stencil Convolution in Haskell
Importing the library
Download the `repa` package:
$ cabal install repa
and import it qualified:
import qualified Data.Array.Repa as R
The library needs to be imported qualified as it shares the same function names as list operations in the Prelude.
Note: Operations that involve writing new index types for Repa arrays will require the '-XTypeOperators' language extension.
For non-core functionality, a number of related packages are available:
- repa-bytestring
- repa-io
- repa-algorithms
- repa-devil (image loading)
and example algorithms in:
Index types and shapes
Before we can get started manipulating arrays, we need a grasp of repa's notion of array shape. Much like the classic 'array' library in Haskell, repa-based arrays are parameterized via a type which determines the dimension of the array, and the type of its index. However, while classic arrays take tuples to represent multiple dimensions, Repa arrays use a richer type language for describing multi-dimensional array indices and shapes (technically, a heterogeneous snoc list).
Shape types are built somewhat like lists. The constructor Z corresponds to a rank zero shape, and is used to mark the end of the list. The :. constructor adds additional dimensions to the shape. So, for example, the shape:
(Z:.3 :.2 :.3)
is the shape of a small 3D array, with shape type
(Z:.Int:.Int:.Int)
The most common dimensions are given by the shorthand names:
type DIM0 = Z
type DIM1 = DIM0 :. Int
type DIM2 = DIM1 :. Int
type DIM3 = DIM2 :. Int
type DIM4 = DIM3 :. Int
type DIM5 = DIM4 :. Int
thus,
Array DIM2 Double
is the type of a two-dimensional array of doubles, indexed via `Int` keys, while
Array Z Double
is a zero-dimension object (i.e. a point) holding a Double.
Many operations over arrays are polymorphic in the shape / dimension
component. Others require operating on the shape itself, rather than
the array. A typeclass, Shape, lets us operate uniformly
over arrays with different shape.
Building shapes
To build values of `shape` type, we can use the Z and :. constructors. Open the ghci and import Repa:
Prelude> :m +Data.Array.Repa
Repa> Z -- the zero-dimension
Z
For arrays of non-zero dimension, we must give a size. Note: a common error is to leave off the type of the size.
Repa> :t Z :. 10
Z :. 10 :: Num head => Z :. head
leading to annoying type errors about unresolved instances, such as:
No instance for (Shape (Z :. head0))
To select the correct instance, you will need to annotate the size literals with their concrete type:
Repa> :t Z :. (10 :: Int)
Z :. (10 :: Int) :: Z :. Int
is the shape of 1D arrays of length 10, indexed via Ints.
Given an array, you can always find its shape by calling extent.
Additional convenience types for selecting particular parts of a shape are also provided (All, Any, Slice etc.) which are covered later in the tutorial.
Working with shapes
That one key operation, extent, gives us many attributes of an array:
-- Extract the shape of the array
extent :: Array sh a -> sh
So, given a 3x3x3 array, of type Array DIM3 Int, we can:
-- build an array
Repa> let x :: Array DIM3 Int; x = fromList (Z :. (3::Int) :. (3::Int) :. (3::Int)) [1..27]
Repa> :t x
x :: Array DIM3 Int
-- query the extent
Repa> extent x
((Z :. 3) :. 3) :. 3
-- compute the rank (number of dimensions)
Repa> let sh = extent x
Repa> rank sh
3
-- compute the size (total number of elements)
> size sh
27
-- extract the elements of the array as a flat vector
Repa> toVector x
fromList [1,2,3,4,5,6,7,8,9,10
,11,12,13,14,15,16,17,18,19
,20,21,22,23,24,25,26,27] :: Data.Vector.Unboxed.Vector
Generating arrays
New repa arrays ("arrays" from here on) can be generated in many ways, and we always begin by importing the Data.Array.Repa module:
$ ghci GHCi, version 7.0.3: http://www.haskell.org/ghc/ :? for help Loading package ghc-prim ... linking ... done. Loading package integer-gmp ... linking ... done. Loading package base ... linking ... done. Loading package ffi-1.0 ... linking ... done. Prelude> :m + Data.Array.Repa
They may be constructed from lists, for example. Here is a one dimensional array of length 10, here, given the shape `(Z :. 10)`:
Repa> let inputs = [1..10] :: [Double]
Repa> let x = fromList (Z :. (10::Int)) inputs
Repa> x
[1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0]
The type of `x` is inferred as:
Repa> :t x
x :: Array (Z :. Int) Double
which we can read as "an array of dimension 1, indexed via Int keys, holding elements of type Double"
We could also have written the type as:
Repa> let x' = fromList (Z :. 10 :: DIM1) inputs
Repa> :t x'
x' :: Array DIM1 Double
The same data may also be treated as a two dimensional array, by changing the shape parameter:
Repa> let x2 = fromList (Z :. (5::Int) :. (2::Int)) inputs
Repa> x2
[1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0]
which has the type:
Repa> :t x2
x2 :: Array ((Z :. Int) :. Int) Double
or, as above, if we define it with the type synonym for 2 dimensional Int- indexed arrays, DIM2:
Repa> let x2' = fromList (Z :. 5 :. 2 :: DIM2) inputs
Repa> x2'
[1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0]
Repa> :t x2'
x2' :: Array DIM2 Double
Building arrays from vectors
It is also possible to build arrays from unboxed vectors, from the 'vector' package:
fromVector :: Shape sh => sh -> Vector a -> Array sh a
New arrays are built by applying a shape to the vector. For example:
Repa> import Data.Vector.Unboxed --recent ghci's support this import syntax
Repa Unboxed> let x = fromVector (Z :. (10::Int)) (enumFromN 0 10)
[0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0]
is a one-dimensional array of doubles. As usual, we can also impose other shapes:
Repa Unboxed> let x = fromVector (Z :. (3::Int) :. (3::Int)) (enumFromN 0 9)
Repa Unboxed> x
[0.0,1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0]
Repa Unboxed> :t x
x :: Array ((Z :. Int) :. Int) Double
to create a 3x3 array.
Generating random arrays
The repa-algorithms package lets us generate new arrays with random data:
-- 3d array of Ints, bounded between 0 and 255.
> randomishIntArray (Z :. (3::Int) :. (3::Int) :. (3::Int)) 0 255 1
[217,42,130,200,216,254
,67,77,152,85,140,226,179
,71,23,17,152,84,47,17,45
,5,88,245,107,214,136]
Reading arrays from files
Using the repa-io package, arrays may be written and read from files in a number of formats:
- as BMP files; and
- in a number of text formats.
with other formats rapidly appearing. For the special case of arrays of Word8 values, the repa-bytestring library supports generating bytestrings in memory.
An example: to write an 2D array to an ascii file:
Repa> :m +Data.Array.Repa.IO.Matrix
Repa Matrix> let x = fromList (Z :. 5 :. 2 :: DIM2) [1..10]
Repa Matrix> writeMatrixToTextFile "test.dat" x
This will result in a file containing:
MATRIX 2 5 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0
In turn, this file may be read back in via readMatrixFromTextFile.
Repa Matrix> xx <- readMatrixFromTextFile "test.dat"
Repa Matrix> xx
[1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0]
Repa Matrix> :t xx
it :: Array DIM2 Double
To process .bmp files, use Data.Array.Repa.IO.BMP, as follows (currently reading only works for 24 bit .bmp):
Data.Array.Repa.IO.BMP> x <- readImageFromBMP "/tmp/test24.bmp"
Reads this .bmp image:

as a 3D array of Word8, which can be further processed.
Note: at the time of writing, there are no binary instances for repa arrays
For image IO in many, many formats, use the repa-devil library.
Copying arrays from pointers
You can also generate new repa arrays by copying data from a pointer, using the repa-bytestring package. Here is an example, using "copyFromPtrWord8":
import Data.Word
import Foreign.Ptr
import qualified Data.Vector.Storable as V
import qualified Data.Array.Repa as R
import Data.Array.Repa
import qualified Data.Array.Repa.ByteString as R
import Data.Array.Repa.IO.DevIL
i, j, k :: Int
(i, j, k) = (255, 255, 4 {-RGBA-})
-- 1d vector, filled with pretty colors
v :: V.Vector Word8
v = V.fromList . take (i * j * k) . cycle $ concat
[ [ r, g, b, 255 ]
| r <- [0 .. 255]
, g <- [0 .. 255]
, b <- [0 .. 255]
]
ptr2repa :: Ptr Word8 -> IO (R.Array R.DIM3 Word8)
ptr2repa p = R.copyFromPtrWord8 (Z :. i :. j :. k) p
main = do
-- copy our 1d vector to a repa 3d array, via a pointer
r <- V.unsafeWith v ptr2repa
runIL $ writeImage "test.png" r
return ()
This fills a vector, converts it to a pointer, then copies that pointer to a 3d array, before writing the result out as this image:

Indexing arrays
To access elements in repa arrays, you provide an array and a shape, to access the element:
(!) :: (Shape sh, Elt a) => Array sh a -> sh -> a
So:
> let x = fromList (Z :. (10::Int)) [1..10]
> x ! (Z :. 2)
3.0
Note that we can't give just a bare literal as the shape, even for one-dimensional arrays, :
> x ! 2
No instance for (Num (Z :. Int))
arising from the literal `2'
as the Z type isn't in the Num class, and Haskell's numeric literals are overloaded.
What if the index is out of bounds, though?
> x ! (Z :. 11)
*** Exception: ./Data/Vector/Generic.hs:222 ((!)): index out of bounds (11,10)
an exception is thrown. An alternative is to use indexing functions that return a Maybe:
(!?) :: (Shape sh, Elt a) => Array sh a -> sh -> Maybe a
An example:
> x !? (Z :. 9)
Just 10.0
> x !? (Z :. 11)
Nothing
Operations on arrays
Besides indexing, there are many regular, list-like operations on arrays. Since many of the names parallel those in the Prelude, we import Repa qualified:
Repa> import qualified Data.Array.Repa as Repa
Maps, zips, filters and folds
We can map over multi-dimensional arrays:
Repa> let x = fromList (Z :. (3::Int) :. (3::Int)) [1..9] Repa> x [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0]
since `map` conflicts with the definition in the Prelude, we have to use it qualified as we requested:
Repa> Repa.map (^2) x [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0]
Maps leave the dimension unchanged.
Repa> extent x (Z :. 3) :. 3 Repa> extent (Repa.map (^2) x) (Z :. 3) :. 3
Folding reduces the inner dimension of the array.
fold :: (Shape sh, Elt a)
=> (a -> a -> a) -> a -> Array (sh :. Int) a -> Array sh a
The 'x' defined above is a 2D array:
Repa> extent x (Z :. 3) :. 3
If we sum each row:
Repa> Repa.fold (+) 0 x [6.0,15.0,24.0]
we get a 1D array instead:
Repa> extent (Repa.fold (+) 0 x) Z :. 3
Similarly, if 'y' is a (3 x 3 x 3) 3D array:
Repa> let y = fromList ((Z :. 3 :. 3 :. 3) :: DIM3) [1..27] Repa> y [1.0,2.0,3.0,4.0,5.0,6.0,7.0,8.0,9.0,10.0,11.0,12.0,13.0,14.0,15.0,16.0,17.0,18.0,19.0,20.0,21.0,22.0,23.0,24.0,25.0,26.0,27.0]
we can fold over the inner dimension:
Repa> Repa.fold (+) 0 y [6.0,15.0,24.0,33.0,42.0,51.0,60.0,69.0,78.0]
yielding a 2D (3 x 3) array in place of our 3D (3 x 3 x 3) array
Repa> extent y ((Z :. 3) :. 3) :. 3 Repa> extent (Repa.fold (+) 0 y) (Z :. 3) :. 3
Two arrays may be combined via zipWith:
zipWith :: (Shape sh, Elt b, Elt c, Elt a) =>
(a -> b -> c) -> Array sh a -> Array sh b -> Array sh c
an example:
Repa> Repa.zipWith (*) x x [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0] Repa> extent it (Z :. 3) :. 3
Repa> Repa.zipWith (*) y y [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0, 100.0,121.0,144.0,169.0,196.0,225.0,256.0,289.0,324.0, 361.0,400.0,441.0,484.0,529.0,576.0,625.0,676.0,729.0] --reformatted Repa> extent it ((Z :. 3) :. 3) :. 3
Numeric operations: negation, addition, subtraction, multiplication
Repa arrays are instances of the Num. This means that
operations on numerical elements are lifted automagically onto arrays of
such elements. For example, (+) on two double values corresponds to
element-wise addition, (+), of the two arrays of doubles:
> let x = fromList (Z :. (10::Int)) [1..10] > x + x [2.0,4.0,6.0,8.0,10.0,12.0,14.0,16.0,18.0,20.0]
Other operations from the Num class work just as well:
> -x [-1.0,-2.0,-3.0,-4.0,-5.0,-6.0,-7.0,-8.0,-9.0,-10.0] > x ^ 3 [1.0,8.0,27.0,64.0,125.0,216.0,343.0,512.0,729.0,1000.0]
> x * x [1.0,4.0,9.0,16.0,25.0,36.0,49.0,64.0,81.0,100.0]
Changing the shape of an array
One of the main advantages of repa-style arrays over other arrays in Haskell is the ability to reshape data without copying. This is achieved via *index-space transformations*.
An example: transposing a 2D array (this example taken from the repa paper). First, the type of the transformation:
transpose2D :: Elt e => Array DIM2 e -> Array DIM2 e
Note that this transform will work on DIM2 arrays holding any elements. Now, to swap rows and columns, we have to modify the shape:
transpose2D a = backpermute (swap e) swap a
where
e = extent a
swap (Z :. i :. j) = Z :. j :. i
The swap function reorders the index space of the array. To do this, we extract the current shape of the array, and write a function that maps the index space from the old array to the new array. That index space function is then passed to backpermute which actually constructs the new array from the old one.
backpermute generates a new array from an old, when given the new shape, and a function that translates between the index space of each array (i.e. a shape transformer).
backpermute :: (Shape sh, Shape sh', Elt a) => sh' -> (sh' -> sh) -> Array sh a -> Array sh' a
Note that the array created is not actually evaluated (we only modified the index space of the array).
Transposition is such a common operation that it is provided by the library:
transpose :: (Shape sh, Elt a)
=> Array ((sh :. Int) :. Int) a -> Array ((sh :. Int) :. Int)
the type indicate that it works on the lowest two dimensions of the array.
Other operations on index spaces include taking slices and joining arrays into larger ones.
Examples
Following are some examples of useful functions that exercise the API.
Example: Rotating an image with backpermute
Flip an image upside down:
import System.Environment
import Data.Word
import Data.Array.Repa hiding ((++))
import Data.Array.Repa.IO.DevIL
main = do
[f] <- getArgs
runIL $ do
v <- readImage f
writeImage ("flip-"++f) (rot180 v)
rot180 :: Array DIM3 Word8 -> Array DIM3 Word8
rot180 g = backpermute e flop g
where
e@(Z :. x :. y :. _) = extent g
flop (Z :. i :. j :. k) =
(Z :. x - i - 1 :. y - j - 1 :. k)
Running this:
$ ghc -O2 --make A.hs $ ./A haskell.jpg
Results in:

Example: matrix-matrix multiplication
A more advanced example from the Repa paper: matrix-matrix multiplication: the result of matrix multiplication is a matrix whose elements are found by multiplying the elements of each row from the first matrix by the associated elements of the same column from the second matrix and summing the result.
if and
then
So we take two, 2D arrays and generate a new array, using our transpose function from earlier:
mmMult :: (Num e, Elt e)
=> Array DIM2 e
-> Array DIM2 e
-> Array DIM2 e
mmMult a b = sum (zipWith (*) aRepl bRepl)
where
t = transpose2D b
aRepl = extend (Z :.All :.colsB :.All) a
bRepl = extend (Z :.rowsA :.All :.All) t
(Z :.colsA :.rowsA) = extent a
(Z :.colsB :.rowsB) = extent b
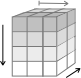
The idea is to expand both 2D argument arrays into 3D arrays by
replicating them across a new axis. The front face of the cuboid that
results represents the array a, which we replicate as often
as b has columns (colsB), producing
aRepl.
The top face represents t (the transposed b), which we
replicate as often as a has rows (rowsA), producing
bRepl,. The two replicated arrays have the same extent,
which corresponds to the index space of matrix multiplication
Optimized implementations of this function are available in the repa-algorithms package.
Example: parallel image desaturation
To convert an image from color to greyscale, we can use the luminosity method to average RGB pixels into a common grey value, where the average is weighted for human perception of green.
The formula for luminosity is 0.21 R + 0.71 G + 0.07 B.
We can write a parallel image desaturation tool using repa and the repa-devil image library:
import Data.Array.Repa.IO.DevIL
import Data.Array.Repa hiding ((++))
import Data.Word
import System.Environment
--
-- Read an image, desaturate, write out with new name.
--
main = do
[f] <- getArgs
runIL $ do
a <- readImage f
let b = traverse a id luminosity
writeImage ("grey-" ++ f) b
And now the luminosity transform itself, which averages the 3 RGB colors based on perceived weight:
--
-- (Parallel) desaturation of an image via the luminosity method.
--
luminosity :: (DIM3 -> Word8) -> DIM3 -> Word8
luminosity _ (Z :. _ :. _ :. 3) = 255 -- alpha channel
luminosity f (Z :. i :. j :. _) = ceiling $ 0.21 * r + 0.71 * g + 0.07 * b
where
r = fromIntegral $ f (Z :. i :. j :. 0)
g = fromIntegral $ f (Z :. i :. j :. 1)
b = fromIntegral $ f (Z :. i :. j :. 2)
And that's it! The result is a parallel image desaturator, when compiled with
$ ghc -O -threaded -rtsopts --make A.hs -fforce-recomp
which we can run, to use two cores:
$ time ./A sunflower.png +RTS -N2 -H ./A sunflower.png +RTS -N2 -H 0.19s user 0.03s system 135% cpu 0.165 total
Given an image like this:

The desaturated result from Haskell: