Difference between revisions of "Typeclassopedia"
m (→Introduction: revert to use of code tag for link to prelude) |
m (fix gmane links using archive.fo) |
||
| (258 intermediate revisions by 33 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ''By [[User:Byorgey|Brent Yorgey]], byorgey@ |
+ | ''By [[User:Byorgey|Brent Yorgey]], byorgey@gmail.com'' |
''Originally published 12 March 2009 in [http://www.haskell.org/wikiupload/8/85/TMR-Issue13.pdf issue 13] of [http://themonadreader.wordpress.com/ the Monad.Reader]. Ported to the Haskell wiki in November 2011 by [[User:Geheimdienst|Geheimdienst]].'' |
''Originally published 12 March 2009 in [http://www.haskell.org/wikiupload/8/85/TMR-Issue13.pdf issue 13] of [http://themonadreader.wordpress.com/ the Monad.Reader]. Ported to the Haskell wiki in November 2011 by [[User:Geheimdienst|Geheimdienst]].'' |
||
| Line 16: | Line 16: | ||
* What the heck is a monoid, and how is it different from a mon<u>a</u>d? |
* What the heck is a monoid, and how is it different from a mon<u>a</u>d? |
||
| − | * I finally figured out how to use [[Parsec]] with do-notation, and someone told me I should use something called < |
+ | * I finally figured out how to use [[Parsec]] with do-notation, and someone told me I should use something called <code>Applicative</code> instead. Um, what? |
| − | * Someone in the [[IRC channel|#haskell]] IRC channel used < |
+ | * Someone in the [[IRC channel|#haskell]] IRC channel used <code>(***)</code>, and when I asked Lambdabot to tell me its type, it printed out scary gobbledygook that didn’t even fit on one line! Then someone used <code>fmap fmap fmap</code> and my brain exploded. |
| − | * When I asked how to do something I thought was really complicated, people started typing things like < |
+ | * When I asked how to do something I thought was really complicated, people started typing things like <code>zip.ap fmap.(id &&& wtf)</code> and the scary thing is that they worked! Anyway, I think those people must actually be robots because there’s no way anyone could come up with that in two seconds off the top of their head. |
If you have, look no further! You, too, can write and understand concise, elegant, idiomatic Haskell code with the best of them. |
If you have, look no further! You, too, can write and understand concise, elegant, idiomatic Haskell code with the best of them. |
||
| Line 29: | Line 29: | ||
It’s impossible to overstate the importance of the first; the patient student of type signatures will uncover many profound secrets. Conversely, anyone ignorant of the types in their code is doomed to eternal uncertainty. “Hmm, it doesn’t compile ... maybe I’ll stick in an |
It’s impossible to overstate the importance of the first; the patient student of type signatures will uncover many profound secrets. Conversely, anyone ignorant of the types in their code is doomed to eternal uncertainty. “Hmm, it doesn’t compile ... maybe I’ll stick in an |
||
| − | < |
+ | <code>fmap</code> here ... nope, let’s see ... maybe I need another <code>(.)</code> somewhere? ... um ...” |
The second key—gaining deep intuition, backed by examples—is also important, but much more difficult to attain. A primary goal of this document is to set you on the road to gaining such intuition. However— |
The second key—gaining deep intuition, backed by examples—is also important, but much more difficult to attain. A primary goal of this document is to set you on the road to gaining such intuition. However— |
||
| Line 37: | Line 37: | ||
This document can only be a starting point, since good intuition comes from hard work, [http://byorgey.wordpress.com/2009/01/12/abstraction-intuition-and-the-monad-tutorial-fallacy/ not from learning the right metaphor]. Anyone who reads and understands all of it will still have an arduous journey ahead—but sometimes a good starting point makes a big difference. |
This document can only be a starting point, since good intuition comes from hard work, [http://byorgey.wordpress.com/2009/01/12/abstraction-intuition-and-the-monad-tutorial-fallacy/ not from learning the right metaphor]. Anyone who reads and understands all of it will still have an arduous journey ahead—but sometimes a good starting point makes a big difference. |
||
| − | It should be noted that this is not a Haskell tutorial; it is assumed that the reader is already familiar with the basics of Haskell, including the standard |
+ | It should be noted that this is not a Haskell tutorial; it is assumed that the reader is already familiar with the basics of Haskell, including the standard [{{HackageDocs|base|Prelude}} <code>Prelude</code>], the type system, data types, and type classes. |
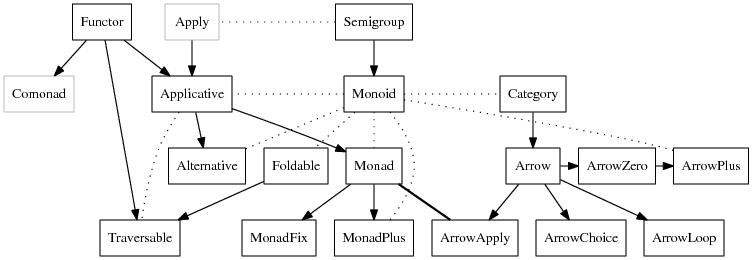
| − | The type classes we will be discussing and their interrelationships: |
+ | The type classes we will be discussing and their interrelationships ([[:File:Dependencies.txt|source code for this graph can be found here]]): |
[[Image:Typeclassopedia-diagram.png]] |
[[Image:Typeclassopedia-diagram.png]] |
||
| − | {{note| |
+ | {{note|<code>Apply</code> can be found in the [http://hackage.haskell.org/package/semigroupoids <code>semigroupoids</code> package], and <code>Comonad</code> in the [http://hackage.haskell.org/package/comonad <code>comonad</code> package].}} |
| − | * <span style="border-bottom: 2px solid black">Solid arrows</span> point from the general to the specific; that is, if there is an arrow from < |
+ | * <span style="border-bottom: 2px solid black">Solid arrows</span> point from the general to the specific; that is, if there is an arrow from <code>Foo</code> to <code>Bar</code> it means that every <code>Bar</code> is (or should be, or can be made into) a <code>Foo</code>. |
| − | * <span style="border-bottom: 2px dotted black">Dotted |
+ | * <span style="border-bottom: 2px dotted black">Dotted lines</span> indicate some other sort of relationship. |
| − | * < |
+ | * <code>Monad</code> and <code>ArrowApply</code> are equivalent. |
| − | * < |
+ | * <code>Apply</code> and <code>Comonad</code> are greyed out since they are not actually (yet?) in the standard Haskell libraries {{noteref}}. |
| − | One more note before we begin. The original spelling of “type class” is with two words, as evidenced by, for example, the [http://haskell.org/onlinereport/ Haskell |
+ | One more note before we begin. The original spelling of “type class” is with two words, as evidenced by, for example, the [http://www.haskell.org/onlinereport/haskell2010/ Haskell 2010 Language Report], early papers on type classes like [http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.103.5639 Type classes in Haskell] and [http://research.microsoft.com/en-us/um/people/simonpj/papers/type-class-design-space/ Type classes: exploring the design space], and [http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.168.4008 Hudak et al.’s history of Haskell]. However, as often happens with two-word phrases that see a lot of use, it has started to show up as one word (“typeclass”) or, rarely, hyphenated (“type-class”). When wearing my prescriptivist hat, I prefer “type class”, but realize (after changing into my descriptivist hat) that there's probably not much I can do about it. |
| − | We now begin with the simplest type class of all: < |
+ | [[Instances of List and Maybe]] illustrates these type classes with simple examples using List and Maybe. We now begin with the simplest type class of all: <code>Functor</code>. |
=Functor= |
=Functor= |
||
| − | The < |
+ | The <code>Functor</code> class ([{{HackageDocs|base|Prelude}}#t:Functor haddock]) is the most basic and ubiquitous type class in the Haskell libraries. A simple intuition is that a <code>Functor</code> represents a “container” of some sort, along with the ability to apply a function uniformly to every element in the container. For example, a list is a container of elements, and we can apply a function to every element of a list, using <code>map</code>. As another example, a binary tree is also a container of elements, and it’s not hard to come up with a way to recursively apply a function to every element in a tree. |
| − | Another intuition is that a < |
+ | Another intuition is that a <code>Functor</code> represents some sort of “computational context”. This intuition is generally more useful, but is more difficult to explain, precisely because it is so general. Some examples later should help to clarify the <code>Functor</code>-as-context point of view. |
| − | In the end, however, a < |
+ | In the end, however, a <code>Functor</code> is simply what it is defined to be; doubtless there are many examples of <code>Functor</code> instances that don’t exactly fit either of the above intuitions. The wise student will focus their attention on definitions and examples, without leaning too heavily on any particular metaphor. Intuition will come, in time, on its own. |
==Definition== |
==Definition== |
||
| − | Here is the type class declaration for < |
+ | Here is the type class declaration for <code>Functor</code>: |
<haskell> |
<haskell> |
||
class Functor f where |
class Functor f where |
||
fmap :: (a -> b) -> f a -> f b |
fmap :: (a -> b) -> f a -> f b |
||
| + | |||
| + | (<$) :: a -> f b -> f a |
||
| + | (<$) = fmap . const |
||
</haskell> |
</haskell> |
||
| + | <code>Functor</code> is exported by the <code>Prelude</code>, so no special imports are needed to use it. Note that the <code>(<$)</code> operator is provided for convenience, with a default implementation in terms of <code>fmap</code>; it is included in the class just to give <code>Functor</code> instances the opportunity to provide a more efficient implementation than the default. To understand <code>Functor</code>, then, we really need to understand <code>fmap</code>. |
||
| − | <hask>Functor</hask> is exported by the <hask>Prelude</hask>, so no special imports are needed to use it. |
||
| + | |||
| + | First, the <code>f a</code> and <code>f b</code> in the type signature for <code>fmap</code> tell us that <code>f</code> isn’t a concrete type like <code>Int</code>; it is a sort of ''type function'' which takes another type as a parameter. More precisely, the ''kind'' of <code>f</code> must be <code>* -> *</code>. For example, <code>Maybe</code> is such a type with kind <code>* -> *</code>: <code>Maybe</code> is not a concrete type by itself (that is, there are no values of type <code>Maybe</code>), but requires another type as a parameter, like <code>Maybe Integer</code>. So it would not make sense to say <code>instance Functor Integer</code>, but it could make sense to say <code>instance Functor Maybe</code>. |
||
| + | Now look at the type of <code>fmap</code>: it takes any function from <code>a</code> to <code>b</code>, and a value of type <code>f a</code>, and outputs a value of type <code>f b</code>. From the container point of view, the intention is that <code>fmap</code> applies a function to each element of a container, without altering the structure of the container. From the context point of view, the intention is that <code>fmap</code> applies a function to a value without altering its context. Let’s look at a few specific examples. |
||
| − | First, the <hask>f a</hask> and <hask>f b</hask> in the type signature for <hask>fmap</hask> tell us that <hask>f</hask> isn’t just a type; it is a ''type constructor'' which takes another type as a parameter. (A more precise way to say this is that the ''kind'' of <hask>f</hask> must be <hask>* -> *</hask>.) For example, <hask>Maybe</hask> is such a type constructor: <hask>Maybe</hask> is not a type in and of itself, but requires another type as a parameter, like <hask>Maybe Integer</hask>. So it would not make sense to say <hask>instance Functor Integer</hask>, but it could make sense to say <hask>instance Functor Maybe</hask>. |
||
| + | Finally, we can understand <code>(<$)</code>: instead of applying a function to the values a container/context, it simply replaces them with a given value. This is the same as applying a constant function, so <code>(<$)</code> can be implemented in terms of <code>fmap</code>. |
||
| − | Now look at the type of <hask>fmap</hask>: it takes any function from <hask>a</hask> to <hask>b</hask>, and a value of type <hask>f a</hask>, and outputs a value of type <hask>f b</hask>. From the container point of view, the intention is that <hask>fmap</hask> applies a function to each element of a container, without altering the structure of the container. From the context point of view, the intention is that <hask>fmap</hask> applies a function to a value without altering its context. Let’s look at a few specific examples. |
||
==Instances== |
==Instances== |
||
| − | {{note|Recall that < |
+ | {{note|Recall that <code>[]</code> has two meanings in Haskell: it can either stand for the empty list, or, as here, it can represent the list type constructor (pronounced “list-of”). In other words, the type <code>[a]</code> (list-of-<code>a</code>) can also be written <code>[] a</code>.}} |
| − | {{note|You might ask why we need a separate < |
+ | {{note|You might ask why we need a separate <code>map</code> function. Why not just do away with the current list-only <code>map</code> function, and rename <code>fmap</code> to <code>map</code> instead? Well, that’s a good question. The usual argument is that someone just learning Haskell, when using <code>map</code> incorrectly, would much rather see an error about lists than about <code>Functor</code>s.}} |
| − | As noted before, the list constructor < |
+ | As noted before, the list constructor <code>[]</code> is a functor {{noteref}}; we can use the standard list function <code>map</code> to apply a function to each element of a list {{noteref}}. The <code>Maybe</code> type constructor is also a functor, representing a container which might hold a single element. The function <code>fmap g</code> has no effect on <code>Nothing</code> (there are no elements to which <code>g</code> can be applied), and simply applies <code>g</code> to the single element inside a <code>Just</code>. Alternatively, under the context interpretation, the list functor represents a context of nondeterministic choice; that is, a list can be thought of as representing a single value which is nondeterministically chosen from among several possibilities (the elements of the list). Likewise, the <code>Maybe</code> functor represents a context with possible failure. These instances are: |
<haskell> |
<haskell> |
||
instance Functor [] where |
instance Functor [] where |
||
| + | fmap :: (a -> b) -> [a] -> [b] |
||
fmap _ [] = [] |
fmap _ [] = [] |
||
fmap g (x:xs) = g x : fmap g xs |
fmap g (x:xs) = g x : fmap g xs |
||
| Line 92: | Line 98: | ||
instance Functor Maybe where |
instance Functor Maybe where |
||
| + | fmap :: (a -> b) -> Maybe a -> Maybe b |
||
fmap _ Nothing = Nothing |
fmap _ Nothing = Nothing |
||
fmap g (Just a) = Just (g a) |
fmap g (Just a) = Just (g a) |
||
</haskell> |
</haskell> |
||
| − | As an aside, in idiomatic Haskell code you will often see the letter < |
+ | As an aside, in idiomatic Haskell code you will often see the letter <code>f</code> used to stand for both an arbitrary <code>Functor</code> and an arbitrary function. In this document, <code>f</code> represents only <code>Functor</code>s, and <code>g</code> or <code>h</code> always represent functions, but you should be aware of the potential confusion. In practice, what <code>f</code> stands for should always be clear from the context, by noting whether it is part of a type or part of the code. |
| − | There are other < |
+ | There are other <code>Functor</code> instances in the standard library as well: |
| − | * < |
+ | * <code>Either e</code> is an instance of <code>Functor</code>; <code>Either e a</code> represents a container which can contain either a value of type <code>a</code>, or a value of type <code>e</code> (often representing some sort of error condition). It is similar to <code>Maybe</code> in that it represents possible failure, but it can carry some extra information about the failure as well. |
| − | * < |
+ | * <code>((,) e)</code> represents a container which holds an “annotation” of type <code>e</code> along with the actual value it holds. It might be clearer to write it as <code>(e,)</code>, by analogy with an operator section like <code>(1+)</code>, but that syntax is not allowed in types (although it is allowed in expressions with the <code>TupleSections</code> extension enabled). However, you can certainly ''think'' of it as <code>(e,)</code>. |
| − | * < |
+ | * <code>((->) e)</code> (which can be thought of as <code>(e ->)</code>; see above), the type of functions which take a value of type <code>e</code> as a parameter, is a <code>Functor</code>. As a container, <code>(e -> a)</code> represents a (possibly infinite) set of values of <code>a</code>, indexed by values of <code>e</code>. Alternatively, and more usefully, <code>((->) e)</code> can be thought of as a context in which a value of type <code>e</code> is available to be consulted in a read-only fashion. This is also why <code>((->) e)</code> is sometimes referred to as the ''reader monad''; more on this later. |
| − | * < |
+ | * <code>IO</code> is a <code>Functor</code>; a value of type <code>IO a</code> represents a computation producing a value of type <code>a</code> which may have I/O effects. If <code>m</code> computes the value <code>x</code> while producing some I/O effects, then <code>fmap g m</code> will compute the value <code>g x</code> while producing the same I/O effects. |
| − | * Many standard types from the [http://hackage.haskell.org/package/containers/ containers library] (such as < |
+ | * Many standard types from the [http://hackage.haskell.org/package/containers/ containers library] (such as <code>Tree</code>, <code>Map</code>, and <code>Sequence</code>) are instances of <code>Functor</code>. A notable exception is <code>Set</code>, which cannot be made a <code>Functor</code> in Haskell (although it is certainly a mathematical functor) since it requires an <code>Ord</code> constraint on its elements; <code>fmap</code> must be applicable to ''any'' types <code>a</code> and <code>b</code>. However, <code>Set</code> (and other similarly restricted data types) can be made an instance of a suitable generalization of <code>Functor</code>, either by [http://archive.fo/9sQhq making <code>a</code> and <code>b</code> arguments to the <code>Functor</code> type class themselves], or by adding an [http://blog.omega-prime.co.uk/?p=127 associated constraint]. |
{{Exercises| |
{{Exercises| |
||
<ol> |
<ol> |
||
| − | <li>Implement < |
+ | <li>Implement <code>Functor</code> instances for <code>Either e</code> and <code>((->) e)</code>.</li> |
| − | <li>Implement < |
+ | <li>Implement <code>Functor</code> instances for <code>((,) e)</code> and for <code>Pair</code>, defined as |
<haskell>data Pair a = Pair a a</haskell> |
<haskell>data Pair a = Pair a a</haskell> |
||
| Line 119: | Line 126: | ||
Explain their similarities and differences. |
Explain their similarities and differences. |
||
</li> |
</li> |
||
| + | <li>Implement a <code>Functor</code> instance for the type <code>ITree</code>, defined as |
||
| − | <li>Give an example of a type which cannot be made an instance of <hask>Functor</hask> (without using <hask>undefined</hask>). |
||
| + | |||
| + | <haskell> |
||
| + | data ITree a = Leaf (Int -> a) |
||
| + | | Node [ITree a] |
||
| + | </haskell> |
||
| + | </li> |
||
| + | <li>Give an example of a type of kind <code>* -> *</code> which cannot be made an instance of <code>Functor</code> (without using <code>undefined</code>). |
||
| + | </li> |
||
| + | <li>Is this statement true or false? |
||
| + | |||
| + | :''The composition of two <code>Functor</code>s is also a <code>Functor</code>.'' |
||
| + | |||
| + | If false, give a counterexample; if true, prove it by exhibiting some appropriate Haskell code. |
||
</li> |
</li> |
||
</ol> |
</ol> |
||
| Line 126: | Line 146: | ||
==Laws== |
==Laws== |
||
| − | As far as the Haskell language itself is concerned, the only requirement to be a < |
+ | As far as the Haskell language itself is concerned, the only requirement to be a <code>Functor</code> is an implementation of <code>fmap</code> with the proper type. Any sensible <code>Functor</code> instance, however, will also satisfy the ''functor laws'', which are part of the definition of a mathematical functor. There are two: |
<haskell> |
<haskell> |
||
| Line 133: | Line 153: | ||
</haskell> |
</haskell> |
||
| − | {{note|Technically, these laws make < |
+ | {{note|Technically, these laws make <code>f</code> and <code>fmap</code> together an endofunctor on ''Hask'', the category of Haskell types (ignoring [[Bottom|⊥]], which is a party pooper). See [http://en.wikibooks.org/wiki/Haskell/Category_theory Wikibook: Category theory].}} |
| − | Together, these laws ensure that < |
+ | Together, these laws ensure that <code>fmap g</code> does not change the ''structure'' of a container, only the elements. Equivalently, and more simply, they ensure that <code>fmap g</code> changes a value without altering its context {{noteref}}. |
The first law says that mapping the identity function over every item in a container has no effect. The second says that mapping a composition of two functions over every item in a container is the same as first mapping one function, and then mapping the other. |
The first law says that mapping the identity function over every item in a container has no effect. The second says that mapping a composition of two functions over every item in a container is the same as first mapping one function, and then mapping the other. |
||
| − | As an example, the following code is a “valid” instance of < |
+ | As an example, the following code is a “valid” instance of <code>Functor</code> (it typechecks), but it violates the functor laws. Do you see why? |
<haskell> |
<haskell> |
||
-- Evil Functor instance |
-- Evil Functor instance |
||
instance Functor [] where |
instance Functor [] where |
||
| + | fmap :: (a -> b) -> [a] -> [b] |
||
fmap _ [] = [] |
fmap _ [] = [] |
||
fmap g (x:xs) = g x : g x : fmap g xs |
fmap g (x:xs) = g x : g x : fmap g xs |
||
| Line 150: | Line 171: | ||
Any Haskeller worth their salt would reject this code as a gruesome abomination. |
Any Haskeller worth their salt would reject this code as a gruesome abomination. |
||
| − | Unlike some other type classes we will encounter, a given type has at most one valid instance of < |
+ | Unlike some other type classes we will encounter, a given type has at most one valid instance of <code>Functor</code>. This [http://archive.fo/U8xIY can be proven] via the [http://homepages.inf.ed.ac.uk/wadler/topics/parametricity.html#free ''free theorem''] for the type of <code>fmap</code>. In fact, [http://byorgey.wordpress.com/2010/03/03/deriving-pleasure-from-ghc-6-12-1/ GHC can automatically derive] <code>Functor</code> instances for many data types. |
| + | |||
| + | {{note|Actually, if <code>seq</code>/<code>undefined</code> are considered, it [http://stackoverflow.com/a/8323243/305559 is possible] to have an implementation which satisfies the first law but not the second. The rest of the comments in this section should be considered in a context where <code>seq</code> and <code>undefined</code> are excluded.}} |
||
| + | |||
| + | A [https://github.com/quchen/articles/blob/master/second_functor_law.md similar argument also shows] that any <code>Functor</code> instance satisfying the first law (<code>fmap id = id</code>) will automatically satisfy the second law as well. Practically, this means that only the first law needs to be checked (usually by a very straightforward induction) to ensure that a <code>Functor</code> instance is valid.{{noteref}} |
||
{{Exercises| |
{{Exercises| |
||
| − | # Although it is not possible for a < |
+ | # Although it is not possible for a <code>Functor</code> instance to satisfy the first <code>Functor</code> law but not the second (excluding <code>undefined</code>), the reverse is possible. Give an example of a (bogus) <code>Functor</code> instance which satisfies the second law but not the first. |
| + | # Which laws are violated by the evil <code>Functor</code> instance for list shown above: both laws, or the first law alone? Give specific counterexamples. |
||
}} |
}} |
||
==Intuition== |
==Intuition== |
||
| − | There are two fundamental ways to think about < |
+ | There are two fundamental ways to think about <code>fmap</code>. The first has already been mentioned: it takes two parameters, a function and a container, and applies the function “inside” the container, producing a new container. Alternately, we can think of <code>fmap</code> as applying a function to a value in a context (without altering the context). |
| − | Just like all other Haskell functions of “more than one parameter”, however, < |
+ | Just like all other Haskell functions of “more than one parameter”, however, <code>fmap</code> is actually ''curried'': it does not really take two parameters, but takes a single parameter and returns a function. For emphasis, we can write <code>fmap</code>’s type with extra parentheses: <code>fmap :: (a -> b) -> (f a -> f b)</code>. Written in this form, it is apparent that <code>fmap</code> transforms a “normal” function (<code>g :: a -> b</code>) into one which operates over containers/contexts (<code>fmap g :: f a -> f b</code>). This transformation is often referred to as a ''lift''; <code>fmap</code> “lifts” a function from the “normal world” into the “<code>f</code> world”. |
| − | == |
+ | ==Utility functions== |
| + | There are a few more <code>Functor</code>-related functions which can be imported from the <code>Data.Functor</code> module. |
||
| − | A good starting point for reading about the category theory behind the concept of a functor is the excellent [http://en.wikibooks.org/wiki/Haskell/Category_theory Haskell wikibook page on category theory]. |
||
| + | * <code>(<$>)</code> is defined as a synonym for <code>fmap</code>. This enables a nice infix style that mirrors the <code>($)</code> operator for function application. For example, <code>f $ 3</code> applies the function <code>f</code> to 3, whereas <code>f <$> [1,2,3]</code> applies <code>f</code> to each member of the list. |
||
| − | =Pointed= |
||
| + | * <code>($>) :: Functor f => f a -> b -> f b</code> is just <code>flip (<$)</code>, and can occasionally be useful. To keep them straight, you can remember that <code>(<$)</code> and <code>($>)</code> point towards the value that will be kept. |
||
| + | * <code>void :: Functor f => f a -> f ()</code> is a specialization of <code>(<$)</code>, that is, <code>void x = () <$ x</code>. This can be used in cases where a computation computes some value but the value should be ignored. |
||
| + | ==Further reading== |
||
| − | {{note|The <hask>Pointed</hask> type class lives in the [http://hackage.haskell.org/package/pointed pointed library], moved from the [http://hackage.haskell.org/package/category-extras category-extras library]. The <hask>point</hask> function was originally named <hask>pure</hask>.<br><br>Edward Kmett, the author of category-extras, pointed, and many related packages, has since moved his focus to [http://hackage.haskell.org/package/semigroupoids semigroupoids] and [http://hackage.haskell.org/package/semigroups semigroups]. He finds them more interesting and useful, and considers <hask>Pointed</hask> to be historical now (he still provides the pointed package only because “people were whinging”). Nevertheless, <hask>Pointed</hask> has kept its value for explaining, and its place in Typeclassopedia. —Geheimdienst, Nov 2011}} |
||
| + | A good starting point for reading about the category theory behind the concept of a functor is the excellent [http://en.wikibooks.org/wiki/Haskell/Category_theory Haskell wikibook page on category theory]. |
||
| − | The <hask>Pointed</hask> type class represents ''pointed functors''. It is not actually a type class in the standard libraries {{noteref}}. But it ''could'' be, and it’s useful in understanding a few other type classes, notably <hask>Applicative</hask> and <hask>Monad</hask>, so let’s pretend for a minute. |
||
| − | |||
| − | Given a <hask>Functor</hask>, the <hask>Pointed</hask> class represents the additional ability to put a value into a “default context”. Often, this corresponds to creating a container with exactly one element, but it is more general than that. The type class declaration for <hask>Pointed</hask> is: |
||
| − | |||
| − | <haskell> |
||
| − | class Functor f => Pointed f where |
||
| − | point :: a -> f a -- aka pure, singleton, return, unit |
||
| − | </haskell> |
||
| − | |||
| − | Most of the standard <hask>Functor</hask> instances could also be instances of <hask>Pointed</hask>—for example, the <hask>Maybe</hask> instance of <hask>Pointed</hask> is <hask>point = Just</hask>; there are many possible implementations for lists, the most natural of which is <hask>point x = [x]</hask>; for <hask>((->) e)</hask> it is ... well, I’ll let you work it out. (Just follow the types!) |
||
| − | |||
| − | One example of a <hask>Functor</hask> which is not <hask>Pointed</hask> is <hask>((,) e)</hask>. If you try implementing <hask>point :: a -> (e,a)</hask> you will quickly see why: since the type <hask>e</hask> is completely arbitrary, there is no way to generate a value of type <hask>e</hask> out of thin air! However, as we will see, <hask>((,) e)</hask> can be made <hask>Pointed</hask> if we place an additional restriction on <hask>e</hask> which allows us to generate a default value of type <hask>e</hask> (the most common solution is to make <hask>e</hask> an instance of <hask>Monoid</hask>). |
||
| − | |||
| − | {{note|For those interested in category theory, this law states precisely that <hask>point</hask> is a natural transformation from the identity functor to <hask>f</hask>.}} The <hask>Pointed</hask> class has only one law {{noteref}}: |
||
| − | |||
| − | <haskell> |
||
| − | fmap g . point = point . g |
||
| − | </haskell> |
||
| − | |||
| − | {{note|... modulo ⊥, <hask>seq</hask>, and assuming a lawful <hask>Functor</hask> instance.}} |
||
| − | |||
| − | However, you need not worry about it: this law is actually a so-called “free theorem” guaranteed by parametricity (see Wadler’s [http://homepages.inf.ed.ac.uk/wadler/topics/parametricity.html#free Theorems for free!]); it’s impossible to write an instance of <hask>Pointed</hask> which does not satisfy it {{noteref}}. |
||
=Applicative= |
=Applicative= |
||
| − | A somewhat newer addition to the pantheon of standard Haskell type classes, ''applicative functors'' represent an abstraction lying |
+ | A somewhat newer addition to the pantheon of standard Haskell type classes, ''applicative functors'' represent an abstraction lying in between <code>Functor</code> and <code>Monad</code> in expressivity, first described by McBride and Paterson. The title of their classic paper, [http://www.soi.city.ac.uk/~ross/papers/Applicative.html Applicative Programming with Effects], gives a hint at the intended intuition behind the [{{HackageDocs|base|Control-Applicative}} <code>Applicative</code>] type class. It encapsulates certain sorts of “effectful” computations in a functionally pure way, and encourages an “applicative” programming style. Exactly what these things mean will be seen later. |
==Definition== |
==Definition== |
||
| − | + | Recall that <code>Functor</code> allows us to lift a “normal” function to a function on computational contexts. But <code>fmap</code> doesn’t allow us to apply a function which is itself in a context to a value in a context. <code>Applicative</code> gives us just such a tool, <code>(<*>)</code> (variously pronounced as "apply", "app", or "splat"). It also provides a method, <code>pure</code>, for embedding values in a default, “effect free” context. Here is the type class declaration for <code>Applicative</code>, as defined in <code>Control.Applicative</code>: |
|
<haskell> |
<haskell> |
||
class Functor f => Applicative f where |
class Functor f => Applicative f where |
||
| − | pure :: a -> f a |
+ | pure :: a -> f a |
| + | infixl 4 <*>, *>, <* |
||
(<*>) :: f (a -> b) -> f a -> f b |
(<*>) :: f (a -> b) -> f a -> f b |
||
| + | |||
| + | (*>) :: f a -> f b -> f b |
||
| + | a1 *> a2 = (id <$ a1) <*> a2 |
||
| + | |||
| + | (<*) :: f a -> f b -> f a |
||
| + | (<*) = liftA2 const |
||
</haskell> |
</haskell> |
||
| − | Note that every < |
+ | Note that every <code>Applicative</code> must also be a <code>Functor</code>. In fact, as we will see, <code>fmap</code> can be implemented using the <code>Applicative</code> methods, so every <code>Applicative</code> is a functor whether we like it or not; the <code>Functor</code> constraint forces us to be honest. |
| + | <code>(*>)</code> and <code>(<*)</code> are provided for convenience, in case a particular instance of <code>Applicative</code> can provide more efficient implementations, but they are provided with default implementations. For more on these operators, see the section on [[#Utility functions|Utility functions]] below. |
||
| − | {{note|Recall that <hask>($)</hask> is just function application: <hask>f $ x {{=}} f x</hask>.}} |
||
| + | {{note|Recall that <code>($)</code> is just function application: <code>f $ x {{=}} f x</code>.}} |
||
| − | As always, it’s crucial to understand the type signature of <hask>(<*>)</hask>. The best way of thinking about it comes from noting that the type of <hask>(<*>)</hask> is similar to the type of <hask>($)</hask> {{noteref}}, but with everything enclosed in an <hask>f</hask>. In other words, <hask>(<*>)</hask> is just function application within a computational context. The type of <hask>(<*>)</hask> is also very similar to the type of <hask>fmap</hask>; the only difference is that the first parameter is <hask>f (a -> b)</hask>, a function in a context, instead of a “normal” function <hask>(a -> b)</hask>. |
||
| + | As always, it’s crucial to understand the type signatures. First, consider <code>(<*>)</code>: the best way of thinking about it comes from noting that the type of <code>(<*>)</code> is similar to the type of <code>($)</code> {{noteref}}, but with everything enclosed in an <code>f</code>. In other words, <code>(<*>)</code> is just function application within a computational context. The type of <code>(<*>)</code> is also very similar to the type of <code>fmap</code>; the only difference is that the first parameter is <code>f (a -> b)</code>, a function in a context, instead of a “normal” function <code>(a -> b)</code>. |
||
| − | Of course, <hask>pure</hask> looks rather familiar. It is the <hask>point</hask> function from the <hask>Pointed</hask> type class. If we actually had it in the standard library, and <hask>pure</hask> appearing under the other name didn’t bother you, then <hask>Applicative</hask> could instead be defined as: |
||
| + | <code>pure</code> takes a value of any type <code>a</code>, and returns a context/container of type <code>f a</code>. The intention is that <code>pure</code> creates some sort of “default” container or “effect free” context. In fact, the behavior of <code>pure</code> is quite constrained by the laws it should satisfy in conjunction with <code>(<*>)</code>. Usually, for a given implementation of <code>(<*>)</code> there is only one possible implementation of <code>pure</code>. |
||
| − | <haskell> |
||
| + | |||
| − | class Pointed f => Applicative' f where |
||
| + | (Note that previous versions of the Typeclassopedia explained <code>pure</code> in terms of a type class <code>Pointed</code>, which can still be found in the [http://hackage.haskell.org/package/pointed <code>pointed</code> package]. However, the current consensus is that <code>Pointed</code> is not very useful after all. For a more detailed explanation, see [[Why not Pointed?]]) |
||
| − | (<*>) :: f (a -> b) -> f a -> f b |
||
| − | </haskell> |
||
==Laws== |
==Laws== |
||
{{note|See |
{{note|See |
||
| − | [ |
+ | [{{HackageDocs|base|Control-Applicative}} haddock for Applicative] and [http://www.soi.city.ac.uk/~ross/papers/Applicative.html Applicative programming with effects]}} |
| + | |||
| + | Traditionally, there are four laws that <code>Applicative</code> instances should satisfy {{noteref}}. In some sense, they are all concerned with making sure that <code>pure</code> deserves its name: |
||
| + | |||
| + | * The identity law:<br /><haskell>pure id <*> v = v</haskell> |
||
| + | * Homomorphism:<br /><haskell>pure f <*> pure x = pure (f x)</haskell>Intuitively, applying a non-effectful function to a non-effectful argument in an effectful context is the same as just applying the function to the argument and then injecting the result into the context with <code>pure</code>. |
||
| + | * Interchange:<br /><haskell>u <*> pure y = pure ($ y) <*> u</haskell>Intuitively, this says that when evaluating the application of an effectful function to a pure argument, the order in which we evaluate the function and its argument doesn't matter. |
||
| + | * Composition:<br /><haskell>u <*> (v <*> w) = pure (.) <*> u <*> v <*> w </haskell>This one is the trickiest law to gain intuition for. In some sense it is expressing a sort of associativity property of <code>(<*>)</code>. The reader may wish to simply convince themselves that this law is type-correct. |
||
| + | |||
| + | Considered as left-to-right rewrite rules, the homomorphism, interchange, and composition laws actually constitute an algorithm for transforming any expression using <code>pure</code> and <code>(<*>)</code> into a canonical form with only a single use of <code>pure</code> at the very beginning and only left-nested occurrences of <code>(<*>)</code>. Composition allows reassociating <code>(<*>)</code>; interchange allows moving occurrences of <code>pure</code> leftwards; and homomorphism allows collapsing multiple adjacent occurrences of <code>pure</code> into one. |
||
| + | There is also a law specifying how <code>Applicative</code> should relate to <code>Functor</code>: |
||
| − | There are several laws that <hask>Applicative</hask> instances should satisfy {{noteref}}, but only one is crucial to developing intuition, because it specifies how <hask>Applicative</hask> should relate to <hask>Functor</hask> (the other four mostly specify the exact sense in which <hask>pure</hask> deserves its name). This law is: |
||
<haskell> |
<haskell> |
||
| Line 231: | Line 253: | ||
</haskell> |
</haskell> |
||
| − | It says that mapping a pure function < |
+ | It says that mapping a pure function <code>g</code> over a context <code>x</code> is the same as first injecting <code>g</code> into a context with <code>pure</code>, and then applying it to <code>x</code> with <code>(<*>)</code>. In other words, we can decompose <code>fmap</code> into two more atomic operations: injection into a context, and application within a context. Since <code>(<$>)</code> is a synonym for <code>fmap</code>, the above law can also be expressed as: |
| − | < |
+ | <code>g <$> x = pure g <*> x</code>. |
| + | |||
| + | {{Exercises| |
||
| + | # (Tricky) One might imagine a variant of the interchange law that says something about applying a pure function to an effectful argument. Using the above laws, prove that<haskell>pure f <*> x = pure (flip ($)) <*> x <*> pure f</haskell> |
||
| + | }} |
||
==Instances== |
==Instances== |
||
| − | Most of the standard types which are instances of < |
+ | Most of the standard types which are instances of <code>Functor</code> are also instances of <code>Applicative</code>. |
| − | < |
+ | <code>Maybe</code> can easily be made an instance of <code>Applicative</code>; writing such an instance is left as an exercise for the reader. |
| − | The list type constructor < |
+ | The list type constructor <code>[]</code> can actually be made an instance of <code>Applicative</code> in two ways; essentially, it comes down to whether we want to think of lists as ordered collections of elements, or as contexts representing multiple results of a nondeterministic computation (see Wadler’s [http://www.springerlink.com/content/y7450255v2670167/ How to replace failure by a list of successes]). |
| − | Let’s first consider the collection point of view. Since there can only be one instance of a given type class for any particular type, one or both of the list instances of < |
+ | Let’s first consider the collection point of view. Since there can only be one instance of a given type class for any particular type, one or both of the list instances of <code>Applicative</code> need to be defined for a <code>newtype</code> wrapper; as it happens, the nondeterministic computation instance is the default, and the collection instance is defined in terms of a <code>newtype</code> called <code>ZipList</code>. This instance is: |
<haskell> |
<haskell> |
||
| Line 249: | Line 275: | ||
instance Applicative ZipList where |
instance Applicative ZipList where |
||
| + | pure :: a -> ZipList a |
||
pure = undefined -- exercise |
pure = undefined -- exercise |
||
| + | |||
| + | (<*>) :: ZipList (a -> b) -> ZipList a -> ZipList b |
||
(ZipList gs) <*> (ZipList xs) = ZipList (zipWith ($) gs xs) |
(ZipList gs) <*> (ZipList xs) = ZipList (zipWith ($) gs xs) |
||
</haskell> |
</haskell> |
||
| − | To apply a list of functions to a list of inputs with < |
+ | To apply a list of functions to a list of inputs with <code>(<*>)</code>, we just match up the functions and inputs elementwise, and produce a list of the resulting outputs. In other words, we “zip” the lists together with function application, <code>($)</code>; hence the name <code>ZipList</code>. |
| − | The other < |
+ | The other <code>Applicative</code> instance for lists, based on the nondeterministic computation point of view, is: |
<haskell> |
<haskell> |
||
instance Applicative [] where |
instance Applicative [] where |
||
| + | pure :: a -> [a] |
||
pure x = [x] |
pure x = [x] |
||
| + | |||
| + | (<*>) :: [a -> b] -> [a] -> [b] |
||
gs <*> xs = [ g x | g <- gs, x <- xs ] |
gs <*> xs = [ g x | g <- gs, x <- xs ] |
||
</haskell> |
</haskell> |
||
| Line 265: | Line 297: | ||
Instead of applying functions to inputs pairwise, we apply each function to all the inputs in turn, and collect all the results in a list. |
Instead of applying functions to inputs pairwise, we apply each function to all the inputs in turn, and collect all the results in a list. |
||
| − | Now we can write nondeterministic computations in a natural style. To add the numbers < |
+ | Now we can write nondeterministic computations in a natural style. To add the numbers <code>3</code> and <code>4</code> deterministically, we can of course write <code>(+) 3 4</code>. But suppose instead of <code>3</code> we have a nondeterministic computation that might result in <code>2</code>, <code>3</code>, or <code>4</code>; then we can write |
<haskell> |
<haskell> |
||
| Line 277: | Line 309: | ||
</haskell> |
</haskell> |
||
| − | There are several other < |
+ | There are several other <code>Applicative</code> instances as well: |
| − | * < |
+ | * <code>IO</code> is an instance of <code>Applicative</code>, and behaves exactly as you would think: to execute <code>m1 <*> m2</code>, first <code>m1</code> is executed, resulting in a function <code>f</code>, then <code>m2</code> is executed, resulting in a value <code>x</code>, and finally the value <code>f x</code> is returned as the result of executing <code>m1 <*> m2</code>. |
| − | * < |
+ | * <code>((,) a)</code> is an <code>Applicative</code>, as long as <code>a</code> is an instance of <code>Monoid</code> ([[#Monoid|section Monoid]]). The <code>a</code> values are accumulated in parallel with the computation. |
| − | * The < |
+ | * The <code>Applicative</code> module defines the <code>Const</code> type constructor; a value of type <code>Const a b</code> simply contains an <code>a</code>. This is an instance of <code>Applicative</code> for any <code>Monoid a</code>; this instance becomes especially useful in conjunction with things like <code>Foldable</code> ([[#Foldable|section Foldable]]). |
| − | * The < |
+ | * The <code>WrappedMonad</code> and <code>WrappedArrow</code> newtypes make any instances of <code>Monad</code> ([[#Monad|section Monad]]) or <code>Arrow</code> ([[#Arrow|section Arrow]]) respectively into instances of <code>Applicative</code>; as we will see when we study those type classes, both are strictly more expressive than <code>Applicative</code>, in the sense that the <code>Applicative</code> methods can be implemented in terms of their methods. |
| + | |||
| + | {{Exercises| |
||
| + | # Implement an instance of <code>Applicative</code> for <code>Maybe</code>. |
||
| + | # Determine the correct definition of <code>pure</code> for the <code>ZipList</code> instance of <code>Applicative</code>—there is only one implementation that satisfies the law relating <code>pure</code> and <code>(<*>)</code>. |
||
| + | }} |
||
==Intuition== |
==Intuition== |
||
| − | McBride and Paterson’s paper introduces the notation <math>[[g \; x_1 \; x_2 \; \cdots \; x_n]]\ </math> to denote function application in a computational context. If each <math>x_i\ </math> has type <math>f \; t_i\ </math> for some applicative functor <math>f\ </math>, and <math>g\ </math> has type <math>t_1 \to t_2 \to \dots \to t_n \to t\ </math>, then the entire expression <math>[[g \; x_1 \; \cdots \; x_n]]\ </math> has type <math>f \; t\ </math>. You can think of this as applying a function to multiple “effectful” arguments. In this sense, the double bracket notation is a generalization of < |
+ | McBride and Paterson’s paper introduces the notation <math>[[g \; x_1 \; x_2 \; \cdots \; x_n]]\ </math> to denote function application in a computational context. If each <math>x_i\ </math> has type <math>f \; t_i\ </math> for some applicative functor <math>f\ </math>, and <math>g\ </math> has type <math>t_1 \to t_2 \to \dots \to t_n \to t\ </math>, then the entire expression <math>[[g \; x_1 \; \cdots \; x_n]]\ </math> has type <math>f \; t\ </math>. You can think of this as applying a function to multiple “effectful” arguments. In this sense, the double bracket notation is a generalization of <code>fmap</code>, which allows us to apply a function to a single argument in a context. |
| − | Why do we need < |
+ | Why do we need <code>Applicative</code> to implement this generalization of <code>fmap</code>? Suppose we use <code>fmap</code> to apply <code>g</code> to the first parameter <code>x1</code>. Then we get something of type <code>f (t2 -> ... t)</code>, but now we are stuck: we can’t apply this function-in-a-context to the next argument with <code>fmap</code>. However, this is precisely what <code>(<*>)</code> allows us to do. |
This suggests the proper translation of the idealized notation <math>[[g \; x_1 \; x_2 \; \cdots \; x_n]]\ </math> into Haskell, namely |
This suggests the proper translation of the idealized notation <math>[[g \; x_1 \; x_2 \; \cdots \; x_n]]\ </math> into Haskell, namely |
||
| Line 298: | Line 335: | ||
</haskell> |
</haskell> |
||
| − | recalling that < |
+ | recalling that <code>Control.Applicative</code> defines <code>(<$>)</code> as convenient infix shorthand for <code>fmap</code>. This is what is meant by an “applicative style”—effectful computations can still be described in terms of function application; the only difference is that we have to use the special operator <code>(<*>)</code> for application instead of simple juxtaposition. |
| + | |||
| + | Note that <code>pure</code> allows embedding “non-effectful” arguments in the middle of an idiomatic application, like |
||
| + | <haskell> |
||
| + | g <$> x1 <*> pure x2 <*> x3 |
||
| + | </haskell> |
||
| + | which has type <code>f d</code>, given |
||
| + | <haskell> |
||
| + | g :: a -> b -> c -> d |
||
| + | x1 :: f a |
||
| + | x2 :: b |
||
| + | x3 :: f c |
||
| + | </haskell> |
||
| + | |||
| + | The double brackets are commonly known as “idiom brackets”, because they allow writing “idiomatic” function application, that is, function application that looks normal but has some special, non-standard meaning (determined by the particular instance of <code>Applicative</code> being used). Idiom brackets are not supported by GHC, but they are supported by the [http://personal.cis.strath.ac.uk/~conor/pub/she/ Strathclyde Haskell Enhancement], a preprocessor which (among many other things) translates idiom brackets into standard uses of <code>(<$>)</code> and <code>(<*>)</code>. This can result in much more readable code when making heavy use of <code>Applicative</code>. |
||
| + | |||
| + | In addition, as of GHC 8, the <code>ApplicativeDo</code> extension enables <code>g <$> x1 <*> x2 <*> ... <*> xn</code> to be written in a different style: |
||
| + | <haskell> |
||
| + | do v1 <- x1 |
||
| + | v2 <- x2 |
||
| + | ... |
||
| + | vn <- xn |
||
| + | pure (g v1 v2 ... vn) |
||
| + | </haskell> |
||
| + | See the Further Reading section below as well as the discussion of do-notation in the Monad section for more information. |
||
| + | |||
| + | ==Utility functions== |
||
| + | |||
| + | <code>Control.Applicative</code> provides several utility functions that work generically with any <code>Applicative</code> instance. |
||
| + | |||
| + | * <code>liftA :: Applicative f => (a -> b) -> f a -> f b</code>. This should be familiar; of course, it is the same as <code>fmap</code> (and hence also the same as <code>(<$>)</code>), but with a more restrictive type. This probably exists to provide a parallel to <code>liftA2</code> and <code>liftA3</code>, but there is no reason you should ever need to use it. |
||
| + | |||
| + | * <code>liftA2 :: Applicative f => (a -> b -> c) -> f a -> f b -> f c</code> lifts a 2-argument function to operate in the context of some <code>Applicative</code>. When <code>liftA2</code> is fully applied, as in <code>liftA2 f arg1 arg2</code>,it is typically better style to instead use <code>f <$> arg1 <*> arg2</code>. However, <code>liftA2</code> can be useful in situations where it is partially applied. For example, one could define a <code>Num</code> instance for <code>Maybe Integer</code> by defining <code>(+) = liftA2 (+)</code> and so on. |
||
| + | |||
| + | * There is a <code>liftA3</code> but no <code>liftAn</code> for larger <code>n</code>. |
||
| + | |||
| + | * <code>(*>) :: Applicative f => f a -> f b -> f b</code> sequences the effects of two <code>Applicative</code> computations, but discards the result of the first. For example, if <code>m1, m2 :: Maybe Int</code>, then <code>m1 *> m2</code> is <code>Nothing</code> whenever either <code>m1</code> or <code>m2</code> is <code>Nothing</code>; but if not, it will have the same value as <code>m2</code>. |
||
| + | |||
| + | * Likewise, <code>(<*) :: Applicative f => f a -> f b -> f a</code> sequences the effects of two computations, but keeps only the result of the first, discarding the result of the second. Just as with <code>(<$)</code> and <code>($>)</code>, to keep <code>(<*)</code> and <code>(*>)</code> straight, remember that they point towards the values that will be kept. |
||
| + | |||
| + | * <code>(<**>) :: Applicative f => f a -> f (a -> b) -> f b</code> is similar to <code>(<*>)</code>, but where the first computation produces value(s) which are provided as input to the function(s) produced by the second computation. Note this is not the same as <code>flip (<*>)</code>, because the effects are performed in the opposite order. This is possible to observe with any <code>Applicative</code> instance with non-commutative effects, such as the instance for lists: <code>(<**>) [1,2] [(+5),(*10)]</code> produces a different result than <code>(flip (<*>))</code> on the same arguments. |
||
| + | |||
| + | * <code>when :: Applicative f => Bool -> f () -> f ()</code> conditionally executes a computation, evaluating to its second argument if the test is <code>True</code>, and to <code>pure ()</code> if the test is <code>False</code>. |
||
| + | |||
| + | * <code>unless :: Applicative f => Bool -> f () -> f ()</code> is like <code>when</code>, but with the test negated. |
||
| + | |||
| + | * The <code>guard</code> function is for use with instances of <code>Alternative</code> (an extension of <code>Applicative</code> to incorporate the ideas of failure and choice), which is discussed in the [[#Failure_and_choice:_Alternative.2C_MonadPlus.2C_ArrowPlus|section on <code>Alternative</code> and friends]]. |
||
| + | |||
| + | {{Exercises| |
||
| + | # Implement a function <haskell>sequenceAL :: Applicative f => [f a] -> f [a]</haskell>. There is a generalized version of this, <code>sequenceA</code>, which works for any <code>Traversable</code> (see the later section on Traversable), but implementing this version specialized to lists is a good exercise. |
||
| + | }} |
||
| + | |||
| + | ==Alternative formulation== |
||
| + | |||
| + | An alternative, equivalent formulation of <code>Applicative</code> is given by |
||
| + | |||
| + | <haskell> |
||
| + | class Functor f => Monoidal f where |
||
| + | unit :: f () |
||
| + | (**) :: f a -> f b -> f (a,b) |
||
| + | </haskell> |
||
| + | |||
| + | {{note|In category-theory speak, we say <code>f</code> is a ''lax'' monoidal functor because there aren't necessarily functions in the other direction, like <code>f (a, b) -> (f a, f b)</code>.}} |
||
| + | Intuitively, this states that a <i>monoidal</i> functor{{noteref}} is one which has some sort of "default shape" and which supports some sort of "combining" operation. <code>pure</code> and <code>(<*>)</code> are equivalent in power to <code>unit</code> and <code>(**)</code> (see the Exercises below). More technically, the idea is that <code>f</code> preserves the "monoidal structure" given by the pairing constructor <code>(,)</code> and unit type <code>()</code>. This can be seen even more clearly if we rewrite the types of <code>unit</code> and <code>(**)</code> as |
||
| + | <haskell> |
||
| + | unit' :: () -> f () |
||
| + | (**') :: (f a, f b) -> f (a, b) |
||
| + | </haskell> |
||
| + | |||
| + | Furthermore, to deserve the name "monoidal" (see the [[#Monoid|section on Monoids]]), instances of <code>Monoidal</code> ought to satisfy the following laws, which seem much more straightforward than the traditional <code>Applicative</code> laws: |
||
| + | |||
| + | {{note|In this and the following laws, <code>≅</code> refers to <i>isomorphism</i> rather than equality. In particular we consider <code>(x,()) ≅ x ≅ ((),x)</code> and <code>((x,y),z) ≅ (x,(y,z))</code>.}} |
||
| + | * Left identity{{noteref}}: <haskell>unit ** v ≅ v</haskell> |
||
| + | * Right identity: <haskell>u ** unit ≅ u</haskell> |
||
| + | * Associativity: <haskell>u ** (v ** w) ≅ (u ** v) ** w</haskell> |
||
| + | |||
| + | These turn out to be equivalent to the usual <code>Applicative</code> laws. In a category theory setting, one would also require a naturality law: |
||
| + | |||
| + | {{note|Here <code>g *** h {{=}} \(x,y) -> (g x, h y)</code>. See [[#Arrow|Arrows]].}} |
||
| + | * Naturality: <haskell>fmap (g *** h) (u ** v) = fmap g u ** fmap h v</haskell> |
||
| + | |||
| + | but in the context of Haskell, this is a free theorem. |
||
| + | |||
| + | Much of this section was taken from [http://blog.ezyang.com/2012/08/applicative-functors/ a blog post by Edward Z. Yang]; see his actual post for a bit more information. |
||
| + | |||
| + | {{Exercises| |
||
| + | # Implement <code>pure</code> and <code>(<*>)</code> in terms of <code>unit</code> and <code>(**)</code>, and vice versa. |
||
| + | # Are there any <code>Applicative</code> instances for which there are also functions <code>f () -> ()</code> and <code>f (a,b) -> (f a, f b)</code>, satisfying some "reasonable" laws? |
||
| + | # (Tricky) Prove that given your implementations from the first exercise, the usual <code>Applicative</code> laws and the <code>Monoidal</code> laws stated above are equivalent. |
||
| + | }} |
||
==Further reading== |
==Further reading== |
||
| + | [http://www.soi.city.ac.uk/~ross/papers/Applicative.html McBride and Paterson’s original paper] is a treasure-trove of information and examples, as well as some perspectives on the connection between <code>Applicative</code> and category theory. Beginners will find it difficult to make it through the entire paper, but it is extremely well-motivated—even beginners will be able to glean something from reading as far as they are able. |
||
| − | There are many other useful combinators in the standard libraries implemented in terms of <hask>pure</hask> and <hask>(<*>)</hask>: for example, <hask>(*>)</hask>, <hask>(<*)</hask>, <hask>(<**>)</hask>, <hask>(<$)</hask>, and so on (see [http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Applicative.html haddock for Applicative]). Judicious use of such secondary combinators can often make code using <hask>Applicative</hask>s much easier to read. |
||
| + | |||
| + | {{note|Introduced by [http://conal.net/papers/simply-reactive/ an earlier paper] that was since superseded by [http://conal.net/papers/push-pull-frp/ Push-pull functional reactive programming].}} |
||
| + | Conal Elliott has been one of the biggest proponents of <code>Applicative</code>. For example, the [http://conal.net/papers/functional-images/ Pan library for functional images] and the reactive library for functional reactive programming (FRP) {{noteref}} make key use of it; his blog also contains [http://conal.net/blog/tag/applicative-functor many examples of <code>Applicative</code> in action]. Building on the work of McBride and Paterson, Elliott also built the [[TypeCompose]] library, which embodies the observation (among others) that <code>Applicative</code> types are closed under composition; therefore, <code>Applicative</code> instances can often be automatically derived for complex types built out of simpler ones. |
||
| − | [http://www.soi.city.ac.uk/~ross/papers/Applicative.html McBride and Paterson’s original paper] is a treasure-trove of information and examples, as well as some perspectives on the connection between <hask>Applicative</hask> and category theory. Beginners will find it difficult to make it through the entire paper, but it is extremely well-motivated—even beginners will be able to glean something from reading as far as they are able. |
||
| + | Although the [http://hackage.haskell.org/package/parsec Parsec parsing library] ([http://legacy.cs.uu.nl/daan/download/papers/parsec-paper.pdf paper]) was originally designed for use as a monad, in its most common use cases an <code>Applicative</code> instance can be used to great effect; [http://www.serpentine.com/blog/2008/02/06/the-basics-of-applicative-functors-put-to-practical-work/ Bryan O’Sullivan’s blog post] is a good starting point. If the extra power provided by <code>Monad</code> isn’t needed, it’s usually a good idea to use <code>Applicative</code> instead. |
||
| − | {{note|Introduced by [http://conal.net/papers/simply-reactive/ an earlier paper] that was since superceded by [http://conal.net/papers/push-pull-frp/ Push-pull functional reactive programming]. —Geheimdienst, Nov 2011}} |
||
| + | A couple other nice examples of <code>Applicative</code> in action include the [http://web.archive.org/web/20090416111947/chrisdone.com/blog/html/2009-02-10-applicative-configfile-hsql.html ConfigFile and HSQL libraries] and the [http://groups.inf.ed.ac.uk/links/formlets/ formlets library]. |
||
| − | Conal Elliott has been one of the biggest proponents of <hask>Applicative</hask>. For example, the [http://conal.net/papers/functional-images/ Pan library for functional images] and the reactive library for functional reactive programming (FRP) {{noteref}} make key use of it; his blog also contains [http://conal.net/blog/tag/applicative-functor many examples of <hask>Applicative</hask> in action]. Building on the work of McBride and Paterson, Elliott also built the [[TypeCompose]] library, which embodies the observation (among others) that <hask>Applicative</hask> types are closed under composition; therefore, <hask>Applicative</hask> instances can often be automatically derived for complex types built out of simpler ones. |
||
| + | Gershom Bazerman's [http://comonad.com/reader/2012/abstracting-with-applicatives/ post] contains many insights into applicatives. |
||
| − | Although the [http://legacy.cs.uu.nl/daan/parsec.html Parsec parsing library] ([http://legacy.cs.uu.nl/daan/download/papers/parsec-paper.pdf paper]) was originally designed for use as a monad, in its most common use cases an <hask>Applicative</hask> instance can be used to great effect; [http://www.serpentine.com/blog/2008/02/06/the-basics-of-applicative-functors-put-to-practical-work/ Bryan O’Sullivan’s blog post] is a good starting point. If the extra power provided by <hask>Monad</hask> isn’t needed, it’s usually a good idea to use <hask>Applicative</hask> instead. |
||
| + | The <code>ApplicativeDo</code> extension is described in [https://ghc.haskell.org/trac/ghc/wiki/ApplicativeDo this wiki page], and in more detail in [http://doi.org/10.1145/2976002.2976007 this Haskell Symposium paper]. |
||
| − | A couple other nice examples of <hask>Applicative</hask> in action include the [http://chrisdone.com/blog/html/2009-02-10-applicative-configfile-hsql.html ConfigFile and HSQL libraries] and the [http://groups.inf.ed.ac.uk/links/formlets/ formlets library]. |
||
=Monad= |
=Monad= |
||
| − | It’s a safe bet that if you’re reading this, you’ve heard of monads—although it’s quite possible you’ve never heard of < |
+ | It’s a safe bet that if you’re reading this, you’ve heard of monads—although it’s quite possible you’ve never heard of <code>Applicative</code> before, or <code>Arrow</code>, or even <code>Monoid</code>. Why are monads such a big deal in Haskell? There are several reasons. |
* Haskell does, in fact, single out monads for special attention by making them the framework in which to construct I/O operations. |
* Haskell does, in fact, single out monads for special attention by making them the framework in which to construct I/O operations. |
||
| − | * Haskell also singles out monads for special attention by providing a special syntactic sugar for monadic expressions: the < |
+ | * Haskell also singles out monads for special attention by providing a special syntactic sugar for monadic expressions: the <code>do</code>-notation. (As of GHC 8, <code>do</code>-notation can be used with <code>Applicative</code> as well, but the notation is still fundamentally related to monads.) |
| − | * < |
+ | * <code>Monad</code> has been around longer than other abstract models of computation such as <code>Applicative</code> or <code>Arrow</code>. |
* The more monad tutorials there are, the harder people think monads must be, and the more new monad tutorials are written by people who think they finally “get” monads (the [http://byorgey.wordpress.com/2009/01/12/abstraction-intuition-and-the-monad-tutorial-fallacy/ monad tutorial fallacy]). |
* The more monad tutorials there are, the harder people think monads must be, and the more new monad tutorials are written by people who think they finally “get” monads (the [http://byorgey.wordpress.com/2009/01/12/abstraction-intuition-and-the-monad-tutorial-fallacy/ monad tutorial fallacy]). |
||
I will let you judge for yourself whether these are good reasons. |
I will let you judge for yourself whether these are good reasons. |
||
| − | In the end, despite all the hoopla, < |
+ | In the end, despite all the hoopla, <code>Monad</code> is just another type class. Let’s take a look at its definition. |
==Definition== |
==Definition== |
||
| + | As of GHC 7.10, [{{HackageDocs|base|Prelude}}#t:Monad <code>Monad</code>] is defined as: |
||
| − | |||
| − | The type class declaration for [http://haskell.org/ghc/docs/latest/html/libraries/base/Prelude.html#t:Monad <hask>Monad</hask>] is: |
||
<haskell> |
<haskell> |
||
| − | class Monad m where |
+ | class Applicative m => Monad m where |
return :: a -> m a |
return :: a -> m a |
||
(>>=) :: m a -> (a -> m b) -> m b |
(>>=) :: m a -> (a -> m b) -> m b |
||
| Line 341: | Line 468: | ||
</haskell> |
</haskell> |
||
| + | (Prior to GHC 7.10, <code>Applicative</code> was not a superclass of <code>Monad</code>, for historical reasons.) |
||
| − | The <hask>Monad</hask> type class is exported by the <hask>Prelude</hask>, along with a few standard instances. However, many utility functions are found in [http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Monad.html <hask>Control.Monad</hask>], and there are also several instances (such as <hask>((->) e)</hask>) defined in [http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Monad-Instances.html <hask>Control.Monad.Instances</hask>]. |
||
| + | The <code>Monad</code> type class is exported by the <code>Prelude</code>, along with a few standard instances. However, many utility functions are found in [{{HackageDocs|base|Control-Monad}} <code>Control.Monad</code>]. |
||
| − | Let’s examine the methods in the <hask>Monad</hask> class one by one. The type of <hask>return</hask> should look familiar; it’s the same as <hask>pure</hask>. Indeed, <hask>return</hask> ''is'' <hask>pure</hask>, but with an unfortunate name. (Unfortunate, since someone coming from an imperative programming background might think that <hask>return</hask> is like the C or Java keyword of the same name, when in fact the similarities are minimal.) From a mathematical point of view, every monad is an applicative functor, but for historical reasons, the <hask>Monad</hask> type class declaration unfortunately does not require this. |
||
| + | Let’s examine the methods in the <code>Monad</code> class one by one. The type of <code>return</code> should look familiar; it’s the same as <code>pure</code>. Indeed, <code>return</code> ''is'' <code>pure</code>, but with an unfortunate name. (Unfortunate, since someone coming from an imperative programming background might think that <code>return</code> is like the C or Java keyword of the same name, when in fact the similarities are minimal.) For historical reasons, we still have both names, but they should always denote the same value (although this cannot be enforced). Likewise, <code>(>>)</code> should be the same as <code>(*>)</code> from <code>Applicative</code>. It is possible that <code>return</code> and <code>(>>)</code> may eventually be removed from the <code>Monad</code> class: see the [https://ghc.haskell.org/trac/ghc/wiki/Proposal/MonadOfNoReturn Monad of No Return proposal]. |
||
| − | We can see that <hask>(>>)</hask> is a specialized version of <hask>(>>=)</hask>, with a default implementation given. It is only included in the type class declaration so that specific instances of <hask>Monad</hask> can override the default implementation of <hask>(>>)</hask> with a more efficient one, if desired. Also, note that although <hask>_ >> n = n</hask> would be a type-correct implementation of <hask>(>>)</hask>, it would not correspond to the intended semantics: the intention is that <hask>m >> n</hask> ignores the ''result'' of <hask>m</hask>, but not its ''effects''. |
||
| + | We can see that <code>(>>)</code> is a specialized version of <code>(>>=)</code>, with a default implementation given. It is only included in the type class declaration so that specific instances of <code>Monad</code> can override the default implementation of <code>(>>)</code> with a more efficient one, if desired. Also, note that although <code>_ >> n = n</code> would be a type-correct implementation of <code>(>>)</code>, it would not correspond to the intended semantics: the intention is that <code>m >> n</code> ignores the ''result'' of <code>m</code>, but not its ''effects''. |
||
| − | The <hask>fail</hask> function is an awful hack that has no place in the <hask>Monad</hask> class; more on this later. |
||
| + | The <code>fail</code> function is an awful hack that has no place in the <code>Monad</code> class; more on this later. |
||
| − | The only really interesting thing to look at—and what makes <hask>Monad</hask> strictly more powerful than <hask>Applicative</hask>—is <hask>(>>=)</hask>, which is often called ''bind''. An alternative definition of <hask>Monad</hask> could look like: |
||
| + | The only really interesting thing to look at—and what makes <code>Monad</code> strictly more powerful than <code>Applicative</code>—is <code>(>>=)</code>, which is often called ''bind''. |
||
| − | <haskell> |
||
| − | class Applicative m => Monad' m where |
||
| − | (>>=) :: m a -> (a -> m b) -> m b |
||
| − | </haskell> |
||
| − | We could spend a while talking about the intuition behind < |
+ | We could spend a while talking about the intuition behind <code>(>>=)</code>—and we will. But first, let’s look at some examples. |
==Instances== |
==Instances== |
||
| − | Even if you don’t understand the intuition behind the < |
+ | Even if you don’t understand the intuition behind the <code>Monad</code> class, you can still create instances of it by just seeing where the types lead you. You may be surprised to find that this actually gets you a long way towards understanding the intuition; at the very least, it will give you some concrete examples to play with as you read more about the <code>Monad</code> class in general. The first few examples are from the standard <code>Prelude</code>; the remaining examples are from the [http://hackage.haskell.org/package/transformers <code>transformers</code> package]. |
| + | |||
| + | <ul> |
||
| + | <li>The simplest possible instance of <code>Monad</code> is [http://hackage.haskell.org/packages/archive/mtl/1.1.0.2/doc/html/Control-Monad-Identity.html <code>Identity</code>], which is described in Dan Piponi’s highly recommended blog post on [http://blog.sigfpe.com/2007/04/trivial-monad.html The Trivial Monad]. Despite being “trivial”, it is a great introduction to the <code>Monad</code> type class, and contains some good exercises to get your brain working. |
||
| + | </li> |
||
| + | <li>The next simplest instance of <code>Monad</code> is <code>Maybe</code>. We already know how to write <code>return</code>/<code>pure</code> for <code>Maybe</code>. So how do we write <code>(>>=)</code>? Well, let’s think about its type. Specializing for <code>Maybe</code>, we have |
||
| − | * The simplest possible instance of <hask>Monad</hask> is [http://hackage.haskell.org/packages/archive/mtl/1.1.0.2/doc/html/Control-Monad-Identity.html <hask>Identity</hask>], which is described in Dan Piponi’s highly recommended blog post on [http://blog.sigfpe.com/2007/04/trivial-monad.html The Trivial Monad]. Despite being “trivial”, it is a great introduction to the <hask>Monad</hask> type class, and contains some good exercises to get your brain working. |
||
| − | * The next simplest instance of <hask>Monad</hask> is <hask>Maybe</hask>. We already know how to write <hask>return</hask>/<hask>pure</hask> for <hask>Maybe</hask>. So how do we write <hask>(>>=)</hask>? Well, let’s think about its type. Specializing for <hask>Maybe</hask>, we have |
||
<haskell> |
<haskell> |
||
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b. |
(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b. |
||
</haskell> |
</haskell> |
||
| − | + | If the first argument to <code>(>>=)</code> is <code>Just x</code>, then we have something of type <code>a</code> (namely, <code>x</code>), to which we can apply the second argument—resulting in a <code>Maybe b</code>, which is exactly what we wanted. What if the first argument to <code>(>>=)</code> is <code>Nothing</code>? In that case, we don’t have anything to which we can apply the <code>a -> Maybe b</code> function, so there’s only one thing we can do: yield <code>Nothing</code>. This instance is: |
|
<haskell> |
<haskell> |
||
instance Monad Maybe where |
instance Monad Maybe where |
||
| + | return :: a -> Maybe a |
||
return = Just |
return = Just |
||
| + | |||
| + | (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b |
||
(Just x) >>= g = g x |
(Just x) >>= g = g x |
||
Nothing >>= _ = Nothing |
Nothing >>= _ = Nothing |
||
</haskell> |
</haskell> |
||
| − | + | We can already get a bit of intuition as to what is going on here: if we build up a computation by chaining together a bunch of functions with <code>(>>=)</code>, as soon as any one of them fails, the entire computation will fail (because <code>Nothing >>= f</code> is <code>Nothing</code>, no matter what <code>f</code> is). The entire computation succeeds only if all the constituent functions individually succeed. So the <code>Maybe</code> monad models computations which may fail. |
|
| + | </li> |
||
| − | + | <li>The <code>Monad</code> instance for the list constructor <code>[]</code> is similar to its <code>Applicative</code> instance; see the exercise below. |
|
| + | </li> |
||
| − | + | <li>Of course, the <code>IO</code> constructor is famously a <code>Monad</code>, but its implementation is somewhat magical, and may in fact differ from compiler to compiler. It is worth emphasizing that the <code>IO</code> monad is the ''only'' monad which is magical. It allows us to build up, in an entirely pure way, values representing possibly effectful computations. The special value <code>main</code>, of type <code>IO ()</code>, is taken by the runtime and actually executed, producing actual effects. Every other monad is functionally pure, and requires no special compiler support. We often speak of monadic values as “effectful computations”, but this is because some monads allow us to write code ''as if'' it has side effects, when in fact the monad is hiding the plumbing which allows these apparent side effects to be implemented in a functionally pure way. |
|
| + | </li> |
||
| − | + | <li>As mentioned earlier, <code>((->) e)</code> is known as the ''reader monad'', since it describes computations in which a value of type <code>e</code> is available as a read-only environment. |
|
| − | + | The [http://hackage.haskell.org/packages/archive/mtl/latest/doc/html/Control-Monad-Reader.html <code>Control.Monad.Reader</code>] module provides the <code>Reader e a</code> type, which is just a convenient <code>newtype</code> wrapper around <code>(e -> a)</code>, along with an appropriate <code>Monad</code> instance and some <code>Reader</code>-specific utility functions such as <code>ask</code> (retrieve the environment), <code>asks</code> (retrieve a function of the environment), and <code>local</code> (run a subcomputation under a different environment). |
|
| + | </li> |
||
| − | + | <li>The [http://hackage.haskell.org/packages/archive/mtl/latest/doc/html/Control-Monad-Writer-Lazy.html <code>Control.Monad.Writer</code>] module provides the <code>Writer</code> monad, which allows information to be collected as a computation progresses. <code>Writer w a</code> is isomorphic to <code>(a,w)</code>, where the output value <code>a</code> is carried along with an annotation or “log” of type <code>w</code>, which must be an instance of <code>Monoid</code> (see [[#Monoid|section Monoid]]); the special function <code>tell</code> performs logging. |
|
| + | </li> |
||
| − | + | <li>The [http://hackage.haskell.org/packages/archive/mtl/latest/doc/html/Control-Monad-State-Lazy.html <code>Control.Monad.State</code>] module provides the <code>State s a</code> type, a <code>newtype</code> wrapper around <code>s -> (a,s)</code>. Something of type <code>State s a</code> represents a stateful computation which produces an <code>a</code> but can access and modify the state of type <code>s</code> along the way. The module also provides <code>State</code>-specific utility functions such as <code>get</code> (read the current state), <code>gets</code> (read a function of the current state), <code>put</code> (overwrite the state), and <code>modify</code> (apply a function to the state). |
|
| + | </li> |
||
| − | + | <li>The [http://hackage.haskell.org/packages/archive/mtl/latest/doc/html/Control-Monad-Cont.html <code>Control.Monad.Cont</code>] module provides the <code>Cont</code> monad, which represents computations in continuation-passing style. It can be used to suspend and resume computations, and to implement non-local transfers of control, co-routines, other complex control structures—all in a functionally pure way. <code>Cont</code> has been called the [http://blog.sigfpe.com/2008/12/mother-of-all-monads.html “mother of all monads”] because of its universal properties. |
|
| + | </li> |
||
| + | </ul> |
||
{{Exercises| |
{{Exercises| |
||
| + | <ol> |
||
| − | # Implement a <hask>Monad</hask> instance for the list constructor, <hask>[]</hask>. Follow the types! |
||
| − | + | <li>Implement a <code>Monad</code> instance for the list constructor, <code>[]</code>. Follow the types!</li> |
|
| + | <li>Implement a <code>Monad</code> instance for <code>((->) e)</code>.</li> |
||
| + | <li>Implement <code>Functor</code> and <code>Monad</code> instances for <code>Free f</code>, defined as |
||
| + | <haskell> |
||
| + | data Free f a = Var a |
||
| + | | Node (f (Free f a)) |
||
| + | </haskell> |
||
| + | You may assume that <code>f</code> has a <code>Functor</code> instance. This is known as the ''free monad'' built from the functor <code>f</code>. |
||
| + | </li> |
||
| + | </ol> |
||
}} |
}} |
||
==Intuition== |
==Intuition== |
||
| − | Let’s look more closely at the type of < |
+ | Let’s look more closely at the type of <code>(>>=)</code>. The basic intuition is that it combines two computations into one larger computation. The first argument, <code>m a</code>, is the first computation. However, it would be boring if the second argument were just an <code>m b</code>; then there would be no way for the computations to interact with one another (actually, this is exactly the situation with <code>Applicative</code>). So, the second argument to <code>(>>=)</code> has type <code>a -> m b</code>: a function of this type, given a ''result'' of the first computation, can produce a second computation to be run. In other words, <code>x >>= k</code> is a computation which runs <code>x</code>, and then uses the result(s) of <code>x</code> to ''decide'' what computation to run second, using the output of the second computation as the result of the entire computation. |
| + | {{note|Actually, because Haskell allows general recursion, one can recursively construct ''infinite'' grammars, and hence <code>Applicative</code> (together with <code>Alternative</code>) is enough to parse any context-sensitive language with a finite alphabet. See [http://byorgey.wordpress.com/2012/01/05/parsing-context-sensitive-languages-with-applicative/ Parsing context-sensitive languages with Applicative].}} |
||
| − | Intuitively, it is this ability to use the output from previous computations to decide what computations to run next that makes <hask>Monad</hask> more powerful than <hask>Applicative</hask>. The structure of an <hask>Applicative</hask> computation is fixed, whereas the structure of a <hask>Monad</hask> computation can change based on intermediate results. |
||
| + | Intuitively, it is this ability to use the output from previous computations to decide what computations to run next that makes <code>Monad</code> more powerful than <code>Applicative</code>. The structure of an <code>Applicative</code> computation is fixed, whereas the structure of a <code>Monad</code> computation can change based on intermediate results. This also means that parsers built using an <code>Applicative</code> interface can only parse context-free languages; in order to parse context-sensitive languages a <code>Monad</code> interface is needed.{{noteref}} |
||
| − | To see the increased power of < |
+ | To see the increased power of <code>Monad</code> from a different point of view, let’s see what happens if we try to implement <code>(>>=)</code> in terms of <code>fmap</code>, <code>pure</code>, and <code>(<*>)</code>. We are given a value <code>x</code> of type <code>m a</code>, and a function <code>k</code> of type <code>a -> m b</code>, so the only thing we can do is apply <code>k</code> to <code>x</code>. We can’t apply it directly, of course; we have to use <code>fmap</code> to lift it over the <code>m</code>. But what is the type of <code>fmap k</code>? Well, it’s <code>m a -> m (m b)</code>. So after we apply it to <code>x</code>, we are left with something of type <code>m (m b)</code>—but now we are stuck; what we really want is an <code>m b</code>, but there’s no way to get there from here. We can ''add'' <code>m</code>’s using <code>pure</code>, but we have no way to ''collapse'' multiple <code>m</code>’s into one. |
| + | {{note|1=You might hear some people claim that the definition in terms of <code>return</code>, <code>fmap</code>, and <code>join</code> is the “math definition” and the definition in terms of <code>return</code> and <code>(>>=)</code> is something specific to Haskell. In fact, both definitions were known in the mathematics community long before Haskell picked up monads.}} |
||
| − | This ability to collapse multiple <hask>m</hask>’s is exactly the ability provided by the function <hask>join :: m (m a) -> m a</hask>, and it should come as no surprise that an alternative definition of <hask>Monad</hask> can be given in terms of <hask>join</hask>: |
||
| + | |||
| + | This ability to collapse multiple <code>m</code>’s is exactly the ability provided by the function <code>join :: m (m a) -> m a</code>, and it should come as no surprise that an alternative definition of <code>Monad</code> can be given in terms of <code>join</code>: |
||
<haskell> |
<haskell> |
||
| Line 413: | Line 563: | ||
</haskell> |
</haskell> |
||
| − | In fact, monads in category theory |
+ | In fact, the canonical definition of monads in category theory is in terms of <code>return</code>, <code>fmap</code>, and <code>join</code> (often called <math>\eta</math>, <math>T</math>, and <math>\mu</math> in the mathematical literature). Haskell uses an alternative formulation with <code>(>>=)</code> instead of <code>join</code> since it is more convenient to use {{noteref}}. However, sometimes it can be easier to think about <code>Monad</code> instances in terms of <code>join</code>, since it is a more “atomic” operation. (For example, <code>join</code> for the list monad is just <code>concat</code>.) |
{{Exercises| |
{{Exercises| |
||
| − | # Implement < |
+ | # Implement <code>(>>{{=}})</code> in terms of <code>fmap</code> (or <code>liftM</code>) and <code>join</code>. |
| − | # Now implement < |
+ | # Now implement <code>join</code> and <code>fmap</code> (<code>liftM</code>) in terms of <code>(>>{{=}})</code> and <code>return</code>. |
}} |
}} |
||
==Utility functions== |
==Utility functions== |
||
| − | The [ |
+ | The [{{HackageDocs|base|Control-Monad}} <code>Control.Monad</code>] module provides a large number of convenient utility functions, all of which can be implemented in terms of the basic <code>Monad</code> operations (<code>return</code> and <code>(>>=)</code> in particular). We have already seen one of them, namely, <code>join</code>. We also mention some other noteworthy ones here; implementing these utility functions oneself is a good exercise. For a more detailed guide to these functions, with commentary and example code, see Henk-Jan van Tuyl’s [http://members.chello.nl/hjgtuyl/tourdemonad.html tour]. |
| + | * <code>liftM :: Monad m => (a -> b) -> m a -> m b</code>. This should be familiar; of course, it is just <code>fmap</code>. The fact that we have both <code>fmap</code> and <code>liftM</code> is a consequence of the fact that the <code>Monad</code> type class did not require a <code>Functor</code> instance until recently, even though mathematically speaking, every monad is a functor. If you are using GHC 7.10 or newer, you should avoid using <code>liftM</code> and just use <code>fmap</code> instead. |
||
| − | {{note|Still, it is unclear how this "bug" should be fixed. Making <hask>Monad</hask> require a <hask>Functor</hask> instance has some drawbacks, as mentioned in this [http://www.haskell.org/pipermail/haskell-prime/2011-January/003312.html 2011 mailing-list discussion]. —Geheimdienst}} |
||
| − | * < |
+ | * <code>ap :: Monad m => m (a -> b) -> m a -> m b</code> should also be familiar: it is equivalent to <code>(<*>)</code>, justifying the claim that the <code>Monad</code> interface is strictly more powerful than <code>Applicative</code>. We can make any <code>Monad</code> into an instance of <code>Applicative</code> by setting <code>pure = return</code> and <code>(<*>) = ap</code>. |
| + | * <code>sequence :: Monad m => [m a] -> m [a]</code> takes a list of computations and combines them into one computation which collects a list of their results. It is again something of a historical accident that <code>sequence</code> has a <code>Monad</code> constraint, since it can actually be implemented only in terms of <code>Applicative</code> (see the exercise at the end of the Utility Functions section for Applicative). Note that the actual type of <code>sequence</code> is more general, and works over any <code>Traversable</code> rather than just lists; see the [[#Traversable|section on <code>Traversable</code>]]. |
||
| − | * <hask>ap :: Monad m => m (a -> b) -> m a -> m b</hask> should also be familiar: it is equivalent to <hask>(<*>)</hask>, justifying the claim that the <hask>Monad</hask> interface is strictly more powerful than <hask>Applicative</hask>. We can make any <hask>Monad</hask> into an instance of <hask>Applicative</hask> by setting <hask>pure = return</hask> and <hask>(<*>) = ap</hask>. |
||
| + | * <code>replicateM :: Monad m => Int -> m a -> m [a]</code> is simply a combination of [{{HackageDocs|base|Prelude}}#v:replicate <code>replicate</code>] and <code>sequence</code>. |
||
| − | * <hask>sequence :: Monad m => [m a] -> m [a]</hask> takes a list of computations and combines them into one computation which collects a list of their results. It is again something of a historical accident that <hask>sequence</hask> has a <hask>Monad</hask> constraint, since it can actually be implemented only in terms of <hask>Applicative</hask>. There is an additional generalization of <hask>sequence</hask> to structures other than lists, which will be discussed in the [[#Traversable|section on <hask>Traversable</hask>]]. |
||
| + | * <code>mapM :: Monad m => (a -> m b) -> [a] -> m [b]</code> maps its first argument over the second, and <code>sequence</code>s the results. The <code>forM</code> function is just <code>mapM</code> with its arguments reversed; it is called <code>forM</code> since it models generalized <code>for</code> loops: the list <code>[a]</code> provides the loop indices, and the function <code>a -> m b</code> specifies the “body” of the loop for each index. Again, these functions actually work over any <code>Traversable</code>, not just lists, and they can also be defined in terms of <code>Applicative</code>, not <code>Monad</code>: the analogue of <code>mapM</code> for <code>Applicative</code> is called <code>traverse</code>. |
||
| − | * <hask>replicateM :: Monad m => Int -> m a -> m [a]</hask> is simply a combination of [http://haskell.org/ghc/docs/latest/html/libraries/base/Prelude.html#v:replicate <hask>replicate</hask>] and <hask>sequence</hask>. |
||
| + | * <code>(=<<) :: Monad m => (a -> m b) -> m a -> m b</code> is just <code>(>>=)</code> with its arguments reversed; sometimes this direction is more convenient since it corresponds more closely to function application. |
||
| − | * <hask>when :: Monad m => Bool -> m () -> m ()</hask> conditionally executes a computation, evaluating to its second argument if the test is <hask>True</hask>, and to <hask>return ()</hask> if the test is <hask>False</hask>. A collection of other sorts of monadic conditionals can be found in the [http://hackage.haskell.org/package/IfElse <hask>IfElse</hask> package]. |
||
| − | * < |
+ | * <code>(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> a -> m c</code> is sort of like function composition, but with an extra <code>m</code> on the result type of each function, and the arguments swapped. We’ll have more to say about this operation later. There is also a flipped variant, <code>(<=<)</code>. |
| + | Many of these functions also have “underscored” variants, such as <code>sequence_</code> and <code>mapM_</code>; these variants throw away the results of the computations passed to them as arguments, using them only for their side effects. |
||
| − | * <hask>(=<<) :: Monad m => (a -> m b) -> m a -> m b</hask> is just <hask>(>>=)</hask> with its arguments reversed; sometimes this direction is more convenient since it corresponds more closely to function application. |
||
| + | Other monadic functions which are occasionally useful include <code>filterM</code>, <code>zipWithM</code>, <code>foldM</code>, and <code>forever</code>. |
||
| − | * <hask>(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> a -> m c</hask> is sort of like function composition, but with an extra <hask>m</hask> on the result type of each function, and the arguments swapped. We’ll have more to say about this operation later. There is also a flipped variant, <hask>(<=<)</hask>. |
||
| − | |||
| − | * The <hask>guard</hask> function is for use with instances of <hask>MonadPlus</hask>, which is discussed at the end of the [[#Monoid|<hask>Monoid</hask> section]]. |
||
| − | |||
| − | Many of these functions also have “underscored” variants, such as <hask>sequence_</hask> and <hask>mapM_</hask>; these variants throw away the results of the computations passed to them as arguments, using them only for their side effects. |
||
| − | |||
| − | Other monadic functions which are occasionally useful include <hask>filterM</hask>, <hask>zipWithM</hask>, <hask>foldM</hask>, and <hask>forever</hask>. |
||
==Laws== |
==Laws== |
||
| − | There are several laws that instances of < |
+ | There are several laws that instances of <code>Monad</code> should satisfy (see also the [[Monad laws]] wiki page). The standard presentation is: |
<haskell> |
<haskell> |
||
| Line 456: | Line 600: | ||
m >>= return = m |
m >>= return = m |
||
m >>= (\x -> k x >>= h) = (m >>= k) >>= h |
m >>= (\x -> k x >>= h) = (m >>= k) >>= h |
||
| − | |||
| − | fmap f xs = xs >>= return . f = liftM f xs |
||
</haskell> |
</haskell> |
||
| − | The first and second laws express the fact that < |
+ | The first and second laws express the fact that <code>return</code> behaves nicely: if we inject a value <code>a</code> into a monadic context with <code>return</code>, and then bind to <code>k</code>, it is the same as just applying <code>k</code> to <code>a</code> in the first place; if we bind a computation <code>m</code> to <code>return</code>, nothing changes. The third law essentially says that <code>(>>=)</code> is associative, sort of. |
| − | {{note|I like to pronounce this operator “fish” |
+ | {{note|I like to pronounce this operator “fish”.}} |
| − | However, the presentation of the above laws, especially the third, is marred by the asymmetry of < |
+ | However, the presentation of the above laws, especially the third, is marred by the asymmetry of <code>(>>=)</code>. It’s hard to look at the laws and see what they’re really saying. I prefer a much more elegant version of the laws, which is formulated in terms of <code>(>=>)</code> {{noteref}}. Recall that <code>(>=>)</code> “composes” two functions of type <code>a -> m b</code> and <code>b -> m c</code>. You can think of something of type <code>a -> m b</code> (roughly) as a function from <code>a</code> to <code>b</code> which may also have some sort of effect in the context corresponding to <code>m</code>. <code>(>=>)</code> lets us compose these “effectful functions”, and we would like to know what properties <code>(>=>)</code> has. The monad laws reformulated in terms of <code>(>=>)</code> are: |
<haskell> |
<haskell> |
||
| Line 472: | Line 614: | ||
</haskell> |
</haskell> |
||
| − | {{note|As fans of category theory will note, these laws say precisely that functions of type < |
+ | {{note|As fans of category theory will note, these laws say precisely that functions of type <code>a -> m b</code> are the arrows of a category with <code>(>{{=}}>)</code> as composition! Indeed, this is known as the ''Kleisli category'' of the monad <code>m</code>. It will come up again when we discuss <code>Arrow</code>s.}} |
| − | Ah, much better! The laws simply state that < |
+ | Ah, much better! The laws simply state that <code>return</code> is the identity of <code>(>=>)</code>, and that <code>(>=>)</code> is associative {{noteref}}. |
| − | There is also a formulation of the monad laws in terms of < |
+ | There is also a formulation of the monad laws in terms of <code>fmap</code>, <code>return</code>, and <code>join</code>; for a discussion of this formulation, see the Haskell [http://en.wikibooks.org/wiki/Haskell/Category_theory wikibook page on category theory]. |
| + | |||
| + | {{Exercises| |
||
| + | # Given the definition <code>g >{{=}}> h {{=}} \x -> g x >>{{=}} h</code>, prove the equivalence of the above laws and the usual monad laws. |
||
| + | }} |
||
| − | ==< |
+ | ==<code>do</code> notation== |
| − | Haskell’s special < |
+ | Haskell’s special <code>do</code> notation supports an “imperative style” of programming by providing syntactic sugar for chains of monadic expressions. The genesis of the notation lies in realizing that something like <code>a >>= \x -> b >> c >>= \y -> d </code> can be more readably written by putting successive computations on separate lines: |
<haskell> |
<haskell> |
||
| Line 489: | Line 635: | ||
</haskell> |
</haskell> |
||
| − | This emphasizes that the overall computation consists of four computations < |
+ | This emphasizes that the overall computation consists of four computations <code>a</code>, <code>b</code>, <code>c</code>, and <code>d</code>, and that <code>x</code> is bound to the result of <code>a</code>, and <code>y</code> is bound to the result of <code>c</code> (<code>b</code>, <code>c</code>, and <code>d</code> are allowed to refer to <code>x</code>, and <code>d</code> is allowed to refer to <code>y</code> as well). From here it is not hard to imagine a nicer notation: |
<haskell> |
<haskell> |
||
| − | do { x <- a |
+ | do { x <- a |
| − | + | ; b |
|
| − | + | ; y <- c |
|
| − | d |
+ | ; d |
} |
} |
||
</haskell> |
</haskell> |
||
| − | (The curly braces and semicolons may optionally be omitted; the Haskell parser uses layout to determine where they should be inserted.) This discussion should make clear that < |
+ | (The curly braces and semicolons may optionally be omitted; the Haskell parser uses layout to determine where they should be inserted.) This discussion should make clear that <code>do</code> notation is just syntactic sugar. In fact, <code>do</code> blocks are recursively translated into monad operations (almost) like this: |
<pre> |
<pre> |
||
| Line 508: | Line 654: | ||
</pre> |
</pre> |
||
| − | This is not quite the whole story, since < |
+ | This is not quite the whole story, since <code>v</code> might be a pattern instead of a variable. For example, one can write |
<haskell> |
<haskell> |
||
| Line 515: | Line 661: | ||
</haskell> |
</haskell> |
||
| − | but what happens if < |
+ | but what happens if <code>foo</code> is an empty list? Well, remember that ugly <code>fail</code> function in the <code>Monad</code> type class declaration? That’s what happens. See [http://www.haskell.org/onlinereport/exps.html#sect3.14 section 3.14 of the Haskell Report] for the full details. See also the discussion of <code>MonadPlus</code> and <code>MonadZero</code> in the [[#Other monoidal classes: Alternative, MonadPlus, ArrowPlus|section on other monoidal classes]]. |
| − | A final note on intuition: < |
+ | A final note on intuition: <code>do</code> notation plays very strongly to the “computational context” point of view rather than the “container” point of view, since the binding notation <code>x <- m</code> is suggestive of “extracting” a single <code>x</code> from <code>m</code> and doing something with it. But <code>m</code> may represent some sort of a container, such as a list or a tree; the meaning of <code>x <- m</code> is entirely dependent on the implementation of <code>(>>=)</code>. For example, if <code>m</code> is a list, <code>x <- m</code> actually means that <code>x</code> will take on each value from the list in turn. |
| + | Sometimes, the full power of <code>Monad</code> is not needed to desugar <code>do</code>-notation. For example, |
||
| − | ==Monad transformers== |
||
| − | |||
| − | One would often like to be able to combine two monads into one: for example, to have stateful, nondeterministic computations (<hask>State</hask> + <hask>[]</hask>), or computations which may fail and can consult a read-only environment (<hask>Maybe</hask> + <hask>Reader</hask>), and so on. Unfortunately, monads do not compose as nicely as applicative functors (yet another reason to use <hask>Applicative</hask> if you don’t need the full power that <hask>Monad</hask> provides), but some monads can be combined in certain ways. |
||
| − | |||
| − | The monad transformer library [http://hackage.haskell.org/package/mtl mtl] provides a number of ''monad transformers'', such as <hask>StateT</hask>, <hask>ReaderT</hask>, <hask>ErrorT</hask> ([http://hackage.haskell.org/packages/archive/mtl/1.1.0.2/doc/html/Control-Monad-Error.html haddock]), and (soon) <hask>MaybeT</hask>, which can be applied to other monads to produce a new monad with the effects of both. For example, <hask>StateT s Maybe</hask> is an instance of <hask>Monad</hask>; computations of type <hask>StateT s Maybe a</hask> may fail, and have access to a mutable state of type <hask>s</hask>. These transformers can be multiply stacked. One thing to keep in mind while using monad transformers is that the order of composition matters. For example, when a <hask>StateT s Maybe a</hask> computation fails, the state ceases being updated; on the other hand, the state of a <hask>MaybeT (State s) a</hask> computation may continue to be modified even after the computation has failed. (This may seem backwards, but it is correct. Monad transformers build composite monads “inside out”; for example, <hask>MaybeT (State s) a</hask> is isomorphic to <hask>s -> (Maybe a, s)</hask>. Lambdabot has an indispensable <hask>@unmtl</hask> command which you can use to “unpack” a monad transformer stack in this way.) |
||
| − | |||
| − | All monad transformers should implement the <hask>MonadTrans</hask> type class, defined in <hask>Control.Monad.Trans</hask>: |
||
<haskell> |
<haskell> |
||
| + | do x <- foo1 |
||
| − | class MonadTrans t where |
||
| + | y <- foo2 |
||
| − | lift :: Monad m => m a -> t m a |
||
| + | z <- foo3 |
||
| + | return (g x y z) |
||
</haskell> |
</haskell> |
||
| + | would normally be desugared to <code>foo1 >>= \x -> foo2 >>= \y -> foo3 >>= \z -> return (g x y z)</code>, but this is equivalent to <code>g <$> foo1 <*> foo2 <*> foo3</code>. With the <code>ApplicativeDo</code> extension enabled (as of GHC 8.0), GHC tries hard to desugar <code>do</code>-blocks using <code>Applicative</code> operations wherever possible. This can sometimes lead to efficiency gains, even for types which also have <code>Monad</code> instances, since in general <code>Applicative</code> computations may be run in parallel, whereas monadic ones may not. For example, consider |
||
| − | It allows arbitrary computations in the base monad <hask>m</hask> to be “lifted” into computations in the transformed monad <hask>t m</hask>. (Note that type application associates to the left, just like function application, so <hask>t m a = (t m) a</hask>. As an exercise, you may wish to work out <hask>t</hask>’s kind, which is rather more interesting than most of the kinds we’ve seen up to this point.) However, you should only have to think about <hask>MonadTrans</hask> when defining your own monad transformers, not when using predefined ones. |
||
| + | <haskell> |
||
| − | {{note|The only problem with this scheme is the quadratic number of instances required as the number of standard monad transformers grows—but as the current set of standard monad transformers seems adequate for most common use cases, this may not be that big of a deal.}} |
||
| + | g :: Int -> Int -> M Int |
||
| + | -- These could be expensive |
||
| − | There are also type classes such as <hask>MonadState</hask>, which provides state-specific methods like <hask>get</hask> and <hask>put</hask>, allowing you to conveniently use these methods not only with <hask>State</hask>, but with any monad which is an instance of <hask>MonadState</hask>—including <hask>MaybeT (State s)</hask>, <hask>StateT s (ReaderT r IO)</hask>, and so on. Similar type classes exist for <hask>Reader</hask>, <hask>Writer</hask>, <hask>Cont</hask>, <hask>IO</hask>, and others {{noteref}}. |
||
| + | bar, baz :: M Int |
||
| + | foo :: M Int |
||
| − | There are two excellent references on monad transformers. Martin Grabmüller’s [http://user.cs.tu-berlin.de/~magr/pub/Transformers.en.html Monad Transformers Step by Step] is a thorough description, with running examples, of how to use monad transformers to elegantly build up computations with various effects. [http://cale.yi.org/index.php/How_To_Use_Monad_Transformers Cale Gibbard’s article] on how to use monad transformers is more practical, describing how to structure code using monad transformers to make writing it as painless as possible. Another good starting place for learning about monad transformers is a [http://blog.sigfpe.com/2006/05/grok-haskell-monad-transformers.html blog post by Dan Piponi]. |
||
| + | foo = do |
||
| + | x <- bar |
||
| + | y <- baz |
||
| + | g x y |
||
| + | </haskell> |
||
| + | <code>foo</code> definitely depends on the <code>Monad</code> instance of <code>M</code>, since the effects generated by the whole computation may depend (via <code>g</code>) on the <code>Int</code> outputs of <code>bar</code> and <code>baz</code>. Nonetheless, with <code>ApplicativeDo</code> enabled, <code>foo</code> can be desugared as |
||
| − | ==MonadFix== |
||
| + | <haskell> |
||
| + | join (g <$> bar <*> baz) |
||
| + | </haskell> |
||
| + | which may allow <code>bar</code> and <code>baz</code> to be computed in parallel, since they at least do not depend on each other. |
||
| + | The <code>ApplicativeDo</code> extension is described in [https://ghc.haskell.org/trac/ghc/wiki/ApplicativeDo this wiki page], and in more detail in [http://doi.org/10.1145/2976002.2976007 this Haskell Symposium paper]. |
||
| − | The <hask>MonadFix</hask> class describes monads which support the special fixpoint operation <hask>mfix :: (a -> m a) -> m a</hask>, which allows the output of monadic computations to be defined via recursion. This is supported in GHC and Hugs by a special “recursive do” notation, <hask>mdo</hask>. For more information, see Levent Erkök’s thesis, [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.15.1543&rep=rep1&type=pdf Value Recursion in Monadic Computations]. |
||
==Further reading== |
==Further reading== |
||
| Line 548: | Line 701: | ||
Philip Wadler was the first to propose using monads to structure functional programs. [http://homepages.inf.ed.ac.uk/wadler/topics/monads.html His paper] is still a readable introduction to the subject. |
Philip Wadler was the first to propose using monads to structure functional programs. [http://homepages.inf.ed.ac.uk/wadler/topics/monads.html His paper] is still a readable introduction to the subject. |
||
| + | {{note|1= |
||
| − | Much of the monad transformer library [http://hackage.haskell.org/package/mtl mtl], including the <hask>Reader</hask>, <hask>Writer</hask>, <hask>State</hask>, and other monads, as well as the monad transformer framework itself, was inspired by Mark Jones’s classic paper [http://web.cecs.pdx.edu/~mpj/pubs/springschool.html Functional Programming with Overloading and Higher-Order Polymorphism]. It’s still very much worth a read—and highly readable—after almost fifteen years. |
||
| + | [[All About Monads]], |
||
| − | |||
| + | [http://www.haskell.org/haskellwiki/Monads_as_Containers Monads as containers], |
||
| − | {{note| |
||
| + | [http://en.wikibooks.org/w/index.php?title=Haskell/Understanding_monads Understanding monads], |
||
| − | [http://www.haskell.org/all_about_monads/html/ All About Monads], |
||
| + | [[The Monadic Way]], |
||
| − | [http://haskell.org/haskellwiki/Monads_as_Containers Monads as containers], |
||
| − | [http://en.wikibooks.org/w/index.php?title=Haskell/Understanding_monads&oldid=933545 Understanding monads], |
||
| − | [[[The Monadic Way]], |
||
[http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html You Could Have Invented Monads! (And Maybe You Already Have.)], |
[http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html You Could Have Invented Monads! (And Maybe You Already Have.)], |
||
[http://www.haskell.org/pipermail/haskell-cafe/2006-November/019190.html there’s a monster in my Haskell!], |
[http://www.haskell.org/pipermail/haskell-cafe/2006-November/019190.html there’s a monster in my Haskell!], |
||
[http://kawagner.blogspot.com/2007/02/understanding-monads-for-real.html Understanding Monads. For real.], |
[http://kawagner.blogspot.com/2007/02/understanding-monads-for-real.html Understanding Monads. For real.], |
||
[http://www.randomhacks.net/articles/2007/03/12/monads-in-15-minutes Monads in 15 minutes: Backtracking and Maybe], |
[http://www.randomhacks.net/articles/2007/03/12/monads-in-15-minutes Monads in 15 minutes: Backtracking and Maybe], |
||
| − | [http://haskell.org/haskellwiki/Monads_as_computation Monads as computation], |
+ | [http://www.haskell.org/haskellwiki/Monads_as_computation Monads as computation], |
[http://metafoo.co.uk/practical-monads.txt Practical Monads]}} |
[http://metafoo.co.uk/practical-monads.txt Practical Monads]}} |
||
There are, of course, numerous monad tutorials of varying quality {{noteref}}. |
There are, of course, numerous monad tutorials of varying quality {{noteref}}. |
||
| − | A few of the best include Cale Gibbard’s [http://haskell.org/haskellwiki/Monads_as_Containers Monads as containers] and [http://haskell.org/haskellwiki/Monads_as_computation Monads as computation]; Jeff Newbern’s [ |
+ | A few of the best include Cale Gibbard’s [http://www.haskell.org/haskellwiki/Monads_as_Containers Monads as containers] and [http://www.haskell.org/haskellwiki/Monads_as_computation Monads as computation]; Jeff Newbern’s [[All About Monads]], a comprehensive guide with lots of examples; and Dan Piponi’s [http://blog.sigfpe.com/2006/08/you-could-have-invented-monads-and.html You Could Have Invented Monads!], which features great exercises. If you just want to know how to use <code>IO</code>, you could consult the [[Introduction to IO]]. Even this is just a sampling; the [[monad tutorials timeline]] is a more complete list. (All these monad tutorials have prompted parodies like [http://koweycode.blogspot.com/2007/01/think-of-monad.html think of a monad ...] as well as other kinds of backlash like [http://ahamsandwich.wordpress.com/2007/07/26/monads-and-why-monad-tutorials-are-all-awful/ Monads! (and Why Monad Tutorials Are All Awful)] or [http://byorgey.wordpress.com/2009/01/12/abstraction-intuition-and-the-monad-tutorial-fallacy/ Abstraction, intuition, and the “monad tutorial fallacy”].) |
| − | Other good monad references which are not necessarily tutorials include [http://members.chello.nl/hjgtuyl/tourdemonad.html Henk-Jan van Tuyl’s tour] of the functions in < |
+ | Other good monad references which are not necessarily tutorials include [http://members.chello.nl/hjgtuyl/tourdemonad.html Henk-Jan van Tuyl’s tour] of the functions in <code>Control.Monad</code>, Dan Piponi’s [http://blog.sigfpe.com/2006/10/monads-field-guide.html field guide], Tim Newsham’s [http://www.thenewsh.com/~newsham/haskell/monad.html What’s a Monad?], and Chris Smith's excellent article [http://cdsmith.wordpress.com/2012/04/18/why-do-monads-matter/ Why Do Monads Matter?]. There are also many blog posts which have been written on various aspects of monads; a collection of links can be found under [[Blog articles/Monads]]. |
| + | For help constructing monads from scratch, and for obtaining a "deep embedding" of monad operations suitable for use in, say, compiling a domain-specific language, see [http://projects.haskell.org/operational Apfelmus's operational package]. |
||
| − | One of the quirks of the <hask>Monad</hask> class and the Haskell type system is that it is not possible to straightforwardly declare <hask>Monad</hask> instances for types which require a class constraint on their data, even if they are monads from a mathematical point of view. For example, <hask>Data.Set</hask> requires an <hask>Ord</hask> constraint on its data, so it cannot be easily made an instance of <hask>Monad</hask>. A solution to this problem was [http://www.randomhacks.net/articles/2007/03/15/data-set-monad-haskell-macros first described by Eric Kidd], and later made into a [http://hackage.haskell.org/cgi-bin/hackage-scripts/package/rmonad library named rmonad] by Ganesh Sittampalam and Peter Gavin. |
||
| + | One of the quirks of the <code>Monad</code> class and the Haskell type system is that it is not possible to straightforwardly declare <code>Monad</code> instances for types which require a class constraint on their data, even if they are monads from a mathematical point of view. For example, <code>Data.Set</code> requires an <code>Ord</code> constraint on its data, so it cannot be easily made an instance of <code>Monad</code>. A solution to this problem was [http://www.randomhacks.net/articles/2007/03/15/data-set-monad-haskell-macros first described by Eric Kidd], and later made into a [http://hackage.haskell.org/cgi-bin/hackage-scripts/package/rmonad library named rmonad] by Ganesh Sittampalam and Peter Gavin. |
||
| − | There are many good reasons for eschewing <hask>do</hask> notation; some have gone so far as to [[Do_notation_considered_harmful|consider it harmful]]. |
||
| + | There are many good reasons for eschewing <code>do</code> notation; some have gone so far as to [[Do_notation_considered_harmful|consider it harmful]]. |
||
| − | Monads can be generalized in various ways; for an exposition of one possibility, see Robert Atkey’s paper on [http://homepages.inf.ed.ac.uk/ratkey/paramnotions-jfp.pdf parameterized monads], or Dan Piponi’s [http://blog.sigfpe.com/2009/02/beyond-monads.html Beyond Monads]. |
||
| + | Monads can be generalized in various ways; for an exposition of one possibility, see Robert Atkey’s paper on [https://bentnib.org/paramnotions-jfp.pdf parameterized monads], or Dan Piponi’s [http://blog.sigfpe.com/2009/02/beyond-monads.html Beyond Monads]. |
||
| − | For the categorically inclined, monads can be viewed as monoids ([http://blog.sigfpe.com/2008/11/from-monoids-to-monads.html From Monoids to Monads]) and also as closure operators [http://blog.plover.com/math/monad-closure.html Triples and Closure]. Derek Elkins’s article in [http://www.haskell.org/wikiupload/8/85/TMR-Issue13.pdf issue 13 of the Monad.Reader] contains an exposition of the category-theoretic underpinnings of some of the standard <hask>Monad</hask> instances, such as <hask>State</hask> and <hask>Cont</hask>. There is also an alternative way to compose monads, using coproducts, as described by [http://doi.acm.org/10.1145/583852.581492 Lüth and Ghani], although this method has not (yet?) seen widespread use. |
||
| + | |||
| + | For the categorically inclined, monads can be viewed as monoids ([http://blog.sigfpe.com/2008/11/from-monoids-to-monads.html From Monoids to Monads]) and also as closure operators ([http://blog.plover.com/math/monad-closure.html Triples and Closure]). Derek Elkins’ article in [http://www.haskell.org/wikiupload/8/85/TMR-Issue13.pdf issue 13 of the Monad.Reader] contains an exposition of the category-theoretic underpinnings of some of the standard <code>Monad</code> instances, such as <code>State</code> and <code>Cont</code>. Jonathan Hill and Keith Clarke have [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.53.6497 an early paper explaining the connection between monads as they arise in category theory and as used in functional programming]. There is also a [http://okmij.org/ftp/Computation/IO-monad-history.html web page by Oleg Kiselyov] explaining the history of the IO monad. |
||
Links to many more research papers related to monads can be found under [[Research papers/Monads and arrows]]. |
Links to many more research papers related to monads can be found under [[Research papers/Monads and arrows]]. |
||
| + | =MonadFail= |
||
| − | =Monoid= |
||
| + | Some monads support a notion of ''failure'', without necessarily supporting the notion of ''recovery'' suggested by <code>MonadPlus</code>, and possibly including a primitive error reporting mechanism. This notion is expressed by the relatively unprincipled <code>MonadFail</code>. When the <code>MonadFailDesugaring</code> language extension is enabled, the <code>fail</code> method from <code>MonadFail</code> is used for pattern match failure in <code>do</code> bindings rather than the traditional <code>fail</code> method of the <code>Monad</code> class. This language change is being implemented because there are many monads, such as <code>Reader</code>, <code>State</code>, <code>Writer</code>, <code>RWST</code>, and <code>Cont</code> that simply do not support a legitimate <code>fail</code> method. |
||
| − | A monoid is a set <math>S\ </math> together with a binary operation <math>\oplus\ </math> which |
||
| + | |||
| + | See the [https://prime.haskell.org/wiki/Libraries/Proposals/MonadFail MonadFail proposal] for more information. |
||
| + | |||
| + | ==Definition== |
||
| + | |||
| + | <haskell> |
||
| + | class Monad m => MonadFail m where |
||
| + | fail :: String -> m a |
||
| + | </haskell> |
||
| + | |||
| + | ==Law== |
||
| + | |||
| + | <haskell> |
||
| + | fail s >>= m = fail s |
||
| + | </haskell> |
||
| + | |||
| + | =Monad transformers= |
||
| + | |||
| + | One would often like to be able to combine two monads into one: for example, to have stateful, nondeterministic computations (<code>State</code> + <code>[]</code>), or computations which may fail and can consult a read-only environment (<code>Maybe</code> + <code>Reader</code>), and so on. Unfortunately, monads do not compose as nicely as applicative functors (yet another reason to use <code>Applicative</code> if you don’t need the full power that <code>Monad</code> provides), but some monads can be combined in certain ways. |
||
| + | |||
| + | ==Standard monad transformers== |
||
| + | |||
| + | The [http://hackage.haskell.org/package/transformers transformers] library provides a number of standard ''monad transformers''. Each monad transformer adds a particular capability/feature/effect to any existing monad. |
||
| + | |||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-Identity.html <code>IdentityT</code>] is the identity transformer, which maps a monad to (something isomorphic to) itself. This may seem useless at first glance, but it is useful for the same reason that the <code>id</code> function is useful -- it can be passed as an argument to things which are parameterized over an arbitrary monad transformer, when you do not actually want any extra capabilities. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-State.html <code>StateT</code>] adds a read-write state. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-Reader.html <code>ReaderT</code>] adds a read-only environment. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-Writer.html <code>WriterT</code>] adds a write-only log. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/0.2.2.0/doc/html/Control-Monad-Trans-RWS.html <code>RWST</code>] conveniently combines <code>ReaderT</code>, <code>WriterT</code>, and <code>StateT</code> into one. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-Maybe.html <code>MaybeT</code>] adds the possibility of failure. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-Error.html <code>ErrorT</code>] adds the possibility of failure with an arbitrary type to represent errors. |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-List.html <code>ListT</code>] adds non-determinism (however, see the discussion of <code>ListT</code> below). |
||
| + | * [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Control-Monad-Trans-Cont.html <code>ContT</code>] adds continuation handling. |
||
| + | |||
| + | For example, <code>StateT s Maybe</code> is an instance of <code>Monad</code>; computations of type <code>StateT s Maybe a</code> may fail, and have access to a mutable state of type <code>s</code>. Monad transformers can be multiply stacked. One thing to keep in mind while using monad transformers is that the order of composition matters. For example, when a <code>StateT s Maybe a</code> computation fails, the state ceases being updated (indeed, it simply disappears); on the other hand, the state of a <code>MaybeT (State s) a</code> computation may continue to be modified even after the computation has "failed". This may seem backwards, but it is correct. Monad transformers build composite monads “inside out”; <code>MaybeT (State s) a</code> is isomorphic to <code>s -> (Maybe a, s)</code>. (Lambdabot has an indispensable <code>@unmtl</code> command which you can use to “unpack” a monad transformer stack in this way.) |
||
| + | Intuitively, the monads become "more fundamental" the further inside the stack you get, and the effects of inner monads "have precedence" over the effects of outer ones. Of course, this is just handwaving, and if you are unsure of the proper order for some monads you wish to combine, there is no substitute for using <code>@unmtl</code> or simply trying out the various options. |
||
| + | |||
| + | ==Definition and laws== |
||
| + | |||
| + | All monad transformers should implement the <code>MonadTrans</code> type class, defined in <code>Control.Monad.Trans.Class</code>: |
||
| + | |||
| + | <haskell> |
||
| + | class MonadTrans t where |
||
| + | lift :: Monad m => m a -> t m a |
||
| + | </haskell> |
||
| + | |||
| + | It allows arbitrary computations in the base monad <code>m</code> to be “lifted” into computations in the transformed monad <code>t m</code>. (Note that type application associates to the left, just like function application, so <code>t m a = (t m) a</code>.) |
||
| + | |||
| + | <code>lift</code> must satisfy the laws |
||
| + | <haskell> |
||
| + | lift . return = return |
||
| + | lift (m >>= f) = lift m >>= (lift . f) |
||
| + | </haskell> |
||
| + | which intuitively state that <code>lift</code> transforms <code>m a</code> computations into <code>t m a</code> computations in a "sensible" way, which sends the <code>return</code> and <code>(>>=)</code> of <code>m</code> to the <code>return</code> and <code>(>>=)</code> of <code>t m</code>. |
||
| + | |||
| + | {{Exercises| |
||
| + | # What is the kind of <code>t</code> in the declaration of <code>MonadTrans</code>? |
||
| + | }} |
||
| + | |||
| + | ==Transformer type classes and "capability" style== |
||
| + | |||
| + | {{note|The only problem with this scheme is the quadratic number of instances required as the number of standard monad transformers grows—but as the current set of standard monad transformers seems adequate for most common use cases, this may not be that big of a deal.}} |
||
| + | |||
| + | There are also type classes (provided by the [http://hackage.haskell.org/package/mtl <code>mtl</code> package]) for the operations of each transformer. For example, the <code>MonadState</code> type class provides the state-specific methods <code>get</code> and <code>put</code>, allowing you to conveniently use these methods not only with <code>State</code>, but with any monad which is an instance of <code>MonadState</code>—including <code>MaybeT (State s)</code>, <code>StateT s (ReaderT r IO)</code>, and so on. Similar type classes exist for <code>Reader</code>, <code>Writer</code>, <code>Cont</code>, <code>IO</code>, and others {{noteref}}. |
||
| + | |||
| + | These type classes serve two purposes. First, they get rid of (most of) the need for explicitly using <code>lift</code>, giving a type-directed way to automatically determine the right number of calls to <code>lift</code>. Simply writing <code>put</code> will be automatically translated into <code>lift . put</code>, <code>lift . lift . put</code>, or something similar depending on what concrete monad stack you are using. |
||
| + | |||
| + | Second, they give you more flexibility to switch between different concrete monad stacks. For example, if you are writing a state-based algorithm, don't write |
||
| + | <haskell> |
||
| + | foo :: State Int Char |
||
| + | foo = modify (*2) >> return 'x' |
||
| + | </haskell> |
||
| + | but rather |
||
| + | <haskell> |
||
| + | foo :: MonadState Int m => m Char |
||
| + | foo = modify (*2) >> return 'x' |
||
| + | </haskell> |
||
| + | Now, if somewhere down the line you realize you need to introduce the possibility of failure, you might switch from <code>State Int</code> to <code>MaybeT (State Int)</code>. The type of the first version of <code>foo</code> would need to be modified to reflect this change, but the second version of <code>foo</code> can still be used as-is. |
||
| + | |||
| + | However, this sort of "capability-based" style (<i>e.g.</i> specifying that <code>foo</code> works for any monad with the "state capability") quickly runs into problems when you try to naively scale it up: for example, what if you need to maintain two independent states? A framework for solving this and related problems is described by Schrijvers and Olivera ([http://users.ugent.be/~tschrijv/Research/papers/icfp2011.pdf Monads, zippers and views: virtualizing the monad stack, ICFP 2011]) and is implemented in the [http://hackage.haskell.org/package/Monatron <code>Monatron</code> package]. |
||
| + | |||
| + | ==Composing monads== |
||
| + | |||
| + | Is the composition of two monads always a monad? As hinted previously, the answer is no. |
||
| + | |||
| + | Since <code>Applicative</code> functors are closed under composition, the problem must lie with <code>join</code>. Indeed, suppose <code>m</code> and <code>n</code> are arbitrary monads; to make a monad out of their composition we would need to be able to implement |
||
| + | <haskell> |
||
| + | join :: m (n (m (n a))) -> m (n a) |
||
| + | </haskell> |
||
| + | but it is not clear how this could be done in general. The <code>join</code> method for <code>m</code> is no help, because the two occurrences of <code>m</code> are not next to each other (and likewise for <code>n</code>). |
||
| + | |||
| + | However, one situation in which it can be done is if <code>n</code> ''distributes'' over <code>m</code>, that is, if there is a function |
||
| + | <haskell> |
||
| + | distrib :: n (m a) -> m (n a) |
||
| + | </haskell> |
||
| + | satisfying certain laws. See Jones and Duponcheel ([http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.42.2605 Composing Monads]); see also the [[#Traversable|section on Traversable]]. |
||
| + | |||
| + | For a much more in-depth discussion and analysis of the failure of monads to be closed under composition, see [http://stackoverflow.com/questions/13034229/concrete-example-showing-that-monads-are-not-closed-under-composition-with-proo?lq=1 this question on StackOverflow]. |
||
| + | |||
| + | {{Exercises| |
||
| + | * Implement <code>join :: M (N (M (N a))) -> M (N a)</code>, given <code>distrib :: N (M a) -> M (N a)</code> and assuming <code>M</code> and <code>N</code> are instances of <code>Monad</code>. |
||
| + | }} |
||
| + | |||
| + | ==Further reading== |
||
| + | |||
| + | Much of the monad transformer library (originally [http://hackage.haskell.org/package/mtl <code>mtl</code>], now split between <code>mtl</code> and [http://hackage.haskell.org/package/transformers <code>transformers</code>]), including the <code>Reader</code>, <code>Writer</code>, <code>State</code>, and other monads, as well as the monad transformer framework itself, was inspired by Mark Jones’ classic paper [http://web.cecs.pdx.edu/~mpj/pubs/springschool.html Functional Programming with Overloading and Higher-Order Polymorphism]. It’s still very much worth a read—and highly readable—after almost fifteen years. |
||
| + | |||
| + | See [http://archive.fo/wxSkj Edward Kmett's mailing list message] for a description of the history and relationships among monad transformer packages (<code>mtl</code>, <code>transformers</code>, <code>monads-fd</code>, <code>monads-tf</code>). |
||
| + | |||
| + | There are two excellent references on monad transformers. Martin Grabmüller’s [https://github.com/mgrabmueller/TransformersStepByStep/blob/master/Transformers.lhs Monad Transformers Step by Step] is a thorough description, with running examples, of how to use monad transformers to elegantly build up computations with various effects. [http://cale.yi.org/index.php/How_To_Use_Monad_Transformers Cale Gibbard’s article] on how to use monad transformers is more practical, describing how to structure code using monad transformers to make writing it as painless as possible. Another good starting place for learning about monad transformers is a [http://blog.sigfpe.com/2006/05/grok-haskell-monad-transformers.html blog post by Dan Piponi]. |
||
| + | |||
| + | The <code>ListT</code> transformer from the <code>transformers</code> package comes with the caveat that <code>ListT m</code> is only a monad when <code>m</code> is ''commutative'', that is, when <code>ma >>= \a -> mb >>= \b -> foo</code> is equivalent to <code>mb >>= \b -> ma >>= \a -> foo</code> (i.e. the order of <code>m</code>'s effects does not matter). For one explanation why, see Dan Piponi's blog post [http://blog.sigfpe.com/2006/11/why-isnt-listt-monad.html "Why isn't <code><nowiki>ListT []</nowiki></code> a monad"]. For more examples, as well as a design for a version of <code>ListT</code> which does not have this problem, see [http://www.haskell.org/haskellwiki/ListT_done_right <code>ListT</code> done right]. |
||
| + | |||
| + | There is an alternative way to compose monads, using coproducts, as described by [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.8.3581 Lüth and Ghani]. This method is interesting but has not (yet?) seen widespread use. For a more recent alternative, see Kiselyov et al's [http://okmij.org/ftp/Haskell/extensible/exteff.pdf Extensible Effects: An Alternative to Monad Transformers]. |
||
| + | |||
| + | =MonadFix= |
||
| + | |||
| + | ''Note: <code>MonadFix</code> is included here for completeness (and because it is interesting) but seems not to be used much. Skipping this section on a first read-through is perfectly OK (and perhaps even recommended).'' |
||
| + | |||
| + | ==<code>do rec</code> notation== |
||
| + | |||
| + | The <code>MonadFix</code> class describes monads which support the special fixpoint operation <code>mfix :: (a -> m a) -> m a</code>, which allows the output of monadic computations to be defined via (effectful) recursion. This is [http://www.haskell.org/ghc/docs/latest/html/users_guide/syntax-extns.html#recursive-do-notation supported in GHC] by a special “recursive do” notation, enabled by the <code>-XRecursiveDo</code> flag. Within a <code>do</code> block, one may have a nested <code>rec</code> block, like so: |
||
| + | <haskell> |
||
| + | do { x <- foo |
||
| + | ; rec { y <- baz |
||
| + | ; z <- bar |
||
| + | ; bob |
||
| + | } |
||
| + | ; w <- frob |
||
| + | } |
||
| + | </haskell> |
||
| + | Normally (if we had <code>do</code> in place of <code>rec</code> in the above example), <code>y</code> would be in scope in <code>bar</code> and <code>bob</code> but not in <code>baz</code>, and <code>z</code> would be in scope only in <code>bob</code>. With the <code>rec</code>, however, <code>y</code> and <code>z</code> are both in scope in all three of <code>baz</code>, <code>bar</code>, and <code>bob</code>. A <code>rec</code> block is analogous to a <code>let</code> block such as |
||
| + | <haskell> |
||
| + | let { y = baz |
||
| + | ; z = bar |
||
| + | } |
||
| + | in bob |
||
| + | </haskell> |
||
| + | because, in Haskell, every variable bound in a <code>let</code>-block is in scope throughout the entire block. (From this point of view, Haskell's normal <code>do</code> blocks are analogous to Scheme's <code>let*</code> construct.) |
||
| + | |||
| + | What could such a feature be used for? One of the motivating examples given in the original paper describing <code>MonadFix</code> (see below) is encoding circuit descriptions. A line in a <code>do</code>-block such as |
||
| + | <haskell> |
||
| + | x <- gate y z |
||
| + | </haskell> |
||
| + | describes a gate whose input wires are labeled <code>y</code> and <code>z</code> and whose output wire is labeled <code>x</code>. Many (most?) useful circuits, however, involve some sort of feedback loop, making them impossible to write in a normal <code>do</code>-block (since some wire would have to be mentioned as an input ''before'' being listed as an output). Using a <code>rec</code> block solves this problem. |
||
| + | |||
| + | ==Examples and intuition== |
||
| + | |||
| + | Of course, not every monad supports such recursive binding. However, as mentioned above, it suffices to have an implementation of <code>mfix :: (a -> m a) -> m a</code>, satisfying a few laws. Let's try implementing <code>mfix</code> for the <code>Maybe</code> monad. That is, we want to implement a function |
||
| + | <haskell> |
||
| + | maybeFix :: (a -> Maybe a) -> Maybe a |
||
| + | </haskell> |
||
| + | {{note|Actually, <code>fix</code> is implemented slightly differently for efficiency reasons; but the given definition is equivalent and simpler for the present purpose.}} |
||
| + | Let's think for a moment about the implementation {{noteref}} of the non-monadic <code>fix :: (a -> a) -> a</code>: |
||
| + | <haskell> |
||
| + | fix f = f (fix f) |
||
| + | </haskell> |
||
| + | Inspired by <code>fix</code>, our first attempt at implementing <code>maybeFix</code> might be something like |
||
| + | <haskell> |
||
| + | maybeFix :: (a -> Maybe a) -> Maybe a |
||
| + | maybeFix f = maybeFix f >>= f |
||
| + | </haskell> |
||
| + | This has the right type. However, something seems wrong: there is nothing in particular here about <code>Maybe</code>; <code>maybeFix</code> actually has the more general type <code>Monad m => (a -> m a) -> m a</code>. But didn't we just say that not all monads support <code>mfix</code>? |
||
| + | |||
| + | The answer is that although this implementation of <code>maybeFix</code> has the right type, it does ''not'' have the intended semantics. If we think about how <code>(>>=)</code> works for the <code>Maybe</code> monad (by pattern-matching on its first argument to see whether it is <code>Nothing</code> or <code>Just</code>) we can see that this definition of <code>maybeFix</code> is completely useless: it will just recurse infinitely, trying to decide whether it is going to return <code>Nothing</code> or <code>Just</code>, without ever even so much as a glance in the direction of <code>f</code>. |
||
| + | |||
| + | The trick is to simply ''assume'' that <code>maybeFix</code> will return <code>Just</code>, and get on with life! |
||
| + | <haskell> |
||
| + | maybeFix :: (a -> Maybe a) -> Maybe a |
||
| + | maybeFix f = ma |
||
| + | where ma = f (fromJust ma) |
||
| + | </haskell> |
||
| + | This says that the result of <code>maybeFix</code> is <code>ma</code>, and assuming that <code>ma = Just x</code>, it is defined (recursively) to be equal to <code>f x</code>. |
||
| + | |||
| + | Why is this OK? Isn't <code>fromJust</code> almost as bad as <code>unsafePerformIO</code>? Well, usually, yes. This is just about the only situation in which it is justified! The interesting thing to note is that <code>maybeFix</code> ''will never crash'' -- although it may, of course, fail to terminate. The only way we could get a crash is if we try to evaluate <code>fromJust ma</code> when we know that <code>ma = Nothing</code>. But how could we know <code>ma = Nothing</code>? Since <code>ma</code> is defined as <code>f (fromJust ma)</code>, it must be that this expression has already been evaluated to <code>Nothing</code> -- in which case there is no reason for us to be evaluating <code>fromJust ma</code> in the first place! |
||
| + | |||
| + | To see this from another point of view, we can consider three possibilities. First, if <code>f</code> outputs <code>Nothing</code> without looking at its argument, then <code>maybeFix f</code> clearly returns <code>Nothing</code>. Second, if <code>f</code> always outputs <code>Just x</code>, where <code>x</code> depends on its argument, then the recursion can proceed usefully: <code>fromJust ma</code> will be able to evaluate to <code>x</code>, thus feeding <code>f</code>'s output back to it as input. Third, if <code>f</code> tries to use its argument to decide whether to output <code>Just</code> or <code>Nothing</code>, then <code>maybeFix f</code> will not terminate: evaluating <code>f</code>'s argument requires evaluating <code>ma</code> to see whether it is <code>Just</code>, which requires evaluating <code>f (fromJust ma)</code>, which requires evaluating <code>ma</code>, ... and so on. |
||
| + | |||
| + | There are also instances of <code>MonadFix</code> for lists (which works analogously to the instance for <code>Maybe</code>), for <code>ST</code>, and for <code>IO</code>. The [http://hackage.haskell.org/packages/archive/base/latest/doc/html/System-IO.html#fixIO instance for <code>IO</code>] is particularly amusing: it creates a new (empty) <code>MVar</code>, immediately reads its contents using <code>unsafeInterleaveIO</code> (which delays the actual reading lazily until the value is needed), uses the contents of the <code>MVar</code> to compute a new value, which it then writes back into the <code>MVar</code>. It almost seems, spookily, that <code>mfix</code> is sending a value back in time to itself through the <code>MVar</code> -- though of course what is really going on is that the reading is delayed just long enough (via <code>unsafeInterleaveIO</code>) to get the process bootstrapped. |
||
| + | |||
| + | {{Exercises| |
||
| + | * Implement a <code>MonadFix</code> instance for <code>[]</code>. |
||
| + | }} |
||
| + | |||
| + | ==<code>mdo</code> syntax== |
||
| + | |||
| + | The example at the start of this section can also be written |
||
| + | |||
| + | <haskell> |
||
| + | mdo { x <- foo |
||
| + | ; y <- baz |
||
| + | ; z <- bar |
||
| + | ; bob |
||
| + | ; w <- frob |
||
| + | } |
||
| + | </haskell> |
||
| + | |||
| + | which will be translated into the original example (assuming that, say, <code>bar</code> and <code>bob</code> refer to <code>y</code>. The difference is that <code>mdo</code> will analyze the code in order to find minimal recursive blocks, which will be placed in <code>rec</code> blocks, whereas <code>rec</code> blocks desugar directly into calls to <code>mfix</code> without any further analysis. |
||
| + | |||
| + | ==Further reading== |
||
| + | |||
| + | For more information (such as the precise desugaring rules for <code>rec</code> blocks), see Levent Erkök and John Launchbury's 2002 Haskell workshop paper, [http://sites.google.com/site/leventerkok/recdo.pdf?attredirects=0 A Recursive do for Haskell], or for full details, Levent Erkök’s thesis, [http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.15.1543&rep=rep1&type=pdf Value Recursion in Monadic Computations]. (Note, while reading, that <code>MonadFix</code> used to be called <code>MonadRec</code>.) You can also read the [http://www.haskell.org/ghc/docs/latest/html/users_guide/syntax-extns.html#recursive-do-notation GHC user manual section on recursive do-notation]. |
||
| + | |||
| + | =Semigroup= |
||
| + | |||
| + | A semigroup is a set <math>S\ </math> together with a binary operation <math>\oplus\ </math> which |
||
combines elements from <math>S\ </math>. The <math>\oplus\ </math> operator is required to be associative |
combines elements from <math>S\ </math>. The <math>\oplus\ </math> operator is required to be associative |
||
(that is, <math>(a \oplus b) \oplus c = a \oplus (b \oplus c)\ </math>, for any |
(that is, <math>(a \oplus b) \oplus c = a \oplus (b \oplus c)\ </math>, for any |
||
| − | <math>a,b,c\ </math> which are elements of <math>S\ </math>) |
+ | <math>a,b,c\ </math> which are elements of <math>S\ </math>). |
| + | |||
| − | <math>S\ </math> which is the identity with respect to <math>\oplus\ </math>. |
||
| + | For example, the natural numbers under addition form a semigroup: the sum of any two natural numbers is a natural number, and <math>(a+b)+c = a+(b+c)\ </math> for any natural numbers <math>a\ </math>, <math>b\ </math>, and <math>c\,\ </math>. The integers under multiplication also form a semigroup, as do the integers (or rationals, or reals) under <math>\max\ </math> or <math>\min\ </math>, Boolean values under conjunction and disjunction, lists under concatenation, functions from a set to itself under composition ... Semigroups show up all over the place, once you know to look for them. |
||
| − | (If you are familiar with group theory, a monoid is like a |
||
| + | |||
| − | group without the requirement that inverses exist.) For example, the |
||
| + | ==Definition== |
||
| − | natural numbers under addition form a monoid: the sum of any two |
||
| + | |||
| − | natural numbers is a natural number; <math>(a+b)+c = a+(b+c)\ </math> for any |
||
| + | As of version 4.9 of the <code>base</code> package (which comes with GHC 8.0), semigroups are defined in the <code>Data.Semigroup</code> module. (If you are working with a previous version of base, or want to write a library that supports previous versions of base, you can use the <code>semigroups</code> package.) |
||
| − | natural numbers <math>a\ </math>, <math>b\ </math>, and <math>c\,\ </math>; and zero is the additive |
||
| + | |||
| − | identity. The integers under multiplication also form a monoid, as do |
||
| + | The definition of the <code>Semigroup</code> type class ([https://hackage.haskell.org/package/base-4.9.0.0/docs/Data-Semigroup.html haddock]) is as follows: |
||
| − | natural numbers under <math>\max\ </math>, Boolean values under conjunction and |
||
| + | |||
| − | disjunction, lists under concatenation, functions from a set to itself |
||
| + | <haskell> |
||
| − | under composition ... Monoids show up all over the place, once you |
||
| + | class Semigroup a where |
||
| − | know to look for them. |
||
| + | (<>) :: a -> a -> a |
||
| + | |||
| + | sconcat :: NonEmpty a -> a |
||
| + | sconcat (a :| as) = go a as where |
||
| + | go b (c:cs) = b <> go c cs |
||
| + | go b [] = b |
||
| + | |||
| + | stimes :: Integral b => b -> a -> a |
||
| + | stimes = ... |
||
| + | </haskell> |
||
| + | |||
| + | The really important method is <code>(<>)</code>, representing the associative binary operation. The other two methods have default implementations in terms of <code>(<>)</code>, and are included in the type class in case some instances can give more efficient implementations than the default. |
||
| + | |||
| + | <code>sconcat</code> reduces a nonempty list using <code>(<>)</code>. For most instances, this is the same as <code>foldr1 (<>)</code>, but it can be constant-time for idempotent semigroups. |
||
| + | |||
| + | <code>stimes n</code> is equivalent to (but sometimes considerably more efficient than) <code>sconcat . replicate n</code>. Its default definition uses multiplication by doubling (also known as exponentiation by squaring). For many semigroups, this is an important optimization; for some, such as lists, it is terrible and must be overridden. |
||
| + | |||
| + | See the [https://hackage.haskell.org/package/base-4.9.0.0/docs/Data-Semigroup.html haddock documentation] for more information on <code>sconcat</code> and <code>stimes</code>. |
||
| + | |||
| + | ==Laws== |
||
| + | |||
| + | The only law is that <code>(<>)</code> must be associative: |
||
| + | |||
| + | <haskell> |
||
| + | (x <> y) <> z = x <> (y <> z) |
||
| + | </haskell> |
||
| + | |||
| + | =Monoid= |
||
| + | |||
| + | Many semigroups have a special element <math>e</math> for which the binary operation <math>\oplus</math> is the identity, that is, <math>e \oplus x = x \oplus e = x</math> for every element <math>x</math>. Such a semigroup-with-identity-element is called a ''monoid''. |
||
==Definition== |
==Definition== |
||
| − | The definition of the < |
+ | The definition of the <code>Monoid</code> type class (defined in |
| − | < |
+ | <code>Data.Monoid</code>; [{{HackageDocs|base|Data-Monoid}} haddock]) is: |
<haskell> |
<haskell> |
||
| Line 610: | Line 999: | ||
</haskell> |
</haskell> |
||
| − | The < |
+ | The <code>mempty</code> value specifies the identity element of the monoid, and <code>mappend</code> |
| − | is the binary operation. The default definition for < |
+ | is the binary operation. The default definition for <code>mconcat</code> |
| − | “reduces” a list of elements by combining them all with < |
+ | “reduces” a list of elements by combining them all with <code>mappend</code>, |
| − | using a right fold. It is only in the < |
+ | using a right fold. It is only in the <code>Monoid</code> class so that specific |
instances have the option of providing an alternative, more efficient |
instances have the option of providing an alternative, more efficient |
||
| − | implementation; usually, you can safely ignore < |
+ | implementation; usually, you can safely ignore <code>mconcat</code> when creating |
| − | a < |
+ | a <code>Monoid</code> instance, since its default definition will work just fine. |
| − | The < |
+ | The <code>Monoid</code> methods are rather unfortunately named; they are inspired |
| − | by the list instance of < |
+ | by the list instance of <code>Monoid</code>, where indeed <code>mempty = []</code> and <code>mappend = (++)</code>, but this is misleading since many |
| − | monoids have little to do with appending (see these [http:// |
+ | monoids have little to do with appending (see these [http://archive.fo/hkTOb Comments from OCaml Hacker Brian Hurt] on the Haskell-cafe mailing list). The situation is made somewhat better by <code>(<>)</code>, which is provided as an alias for <code>mappend</code>. |
| + | |||
| + | Note that the <code>(<>)</code> alias for <code>mappend</code> conflicts with the <code>Semigroup</code> method of the same name. For this reason, <code>Data.Semigroup</code> re-exports much of <code>Data.Monoid</code>; to use semigroups and monoids together, just import <code>Data.Semigroup</code>, and make sure all your types have both <code>Semigroup</code> and <code>Monoid</code> instances (and that <code>(<>) = mappend</code>). |
||
==Laws== |
==Laws== |
||
| − | Of course, every < |
+ | Of course, every <code>Monoid</code> instance should actually be a monoid in the |
mathematical sense, which implies these laws: |
mathematical sense, which implies these laws: |
||
| Line 635: | Line 1,026: | ||
==Instances== |
==Instances== |
||
| − | There are quite a few interesting < |
+ | There are quite a few interesting <code>Monoid</code> instances defined in <code>Data.Monoid</code>. |
<ul> |
<ul> |
||
| − | <li>< |
+ | <li><code>[a]</code> is a <code>Monoid</code>, with <code>mempty = []</code> and <code>mappend = (++)</code>. It is not hard to check that <code>(x ++ y) ++ z = x ++ (y ++ z)</code> for any lists <code>x</code>, <code>y</code>, and <code>z</code>, and that the empty list is the identity: <code>[] ++ x = x ++ [] = x</code>.</li> |
| − | <li>As noted previously, we can make a monoid out of any numeric type under either addition or multiplication. However, since we can’t have two instances for the same type, < |
+ | <li>As noted previously, we can make a monoid out of any numeric type under either addition or multiplication. However, since we can’t have two instances for the same type, <code>Data.Monoid</code> provides two <code>newtype</code> wrappers, <code>Sum</code> and <code>Product</code>, with appropriate <code>Monoid</code> instances. |
<haskell> |
<haskell> |
||
| Line 650: | Line 1,041: | ||
This example code is silly, of course; we could just write |
This example code is silly, of course; we could just write |
||
| − | < |
+ | <code>sum [1..5]</code> and <code>product [1..5]</code>. Nevertheless, these instances are useful in more generalized settings, as we will see in the [[Foldable|section on <code>Foldable</code>]].</li> |
| − | <li>< |
+ | <li><code>Any</code> and <code>All</code> are <code>newtype</code> wrappers providing <code>Monoid</code> instances for <code>Bool</code> (under disjunction and conjunction, respectively).</li> |
| − | <li> There are three instances for < |
+ | <li> There are three instances for <code>Maybe</code>: a basic instance which lifts a <code>Monoid</code> instance for <code>a</code> to an instance for <code>Maybe a</code>, and two <code>newtype</code> wrappers <code>First</code> and <code>Last</code> for which <code>mappend</code> selects the first (respectively last) non-<code>Nothing</code> item.</li> |
| − | <li>< |
+ | <li><code>Endo a</code> is a newtype wrapper for functions <code>a -> a</code>, which form a monoid under composition.</li> |
| − | <li>There are several ways to “lift” < |
+ | <li>There are several ways to “lift” <code>Monoid</code> instances to instances with additional structure. We have already seen that an instance for <code>a</code> can be lifted to an instance for <code>Maybe a</code>. There are also tuple instances: if <code>a</code> and <code>b</code> are instances of <code>Monoid</code>, then so is <code>(a,b)</code>, using the monoid operations for <code>a</code> and <code>b</code> in the obvious pairwise manner. Finally, if <code>a</code> is a <code>Monoid</code>, then so is the function type <code>e -> a</code> for any <code>e</code>; in particular, <code>g `mappend` h</code> is the function which applies both <code>g</code> and <code>h</code> to its argument and then combines the results using the underlying <code>Monoid</code> instance for <code>a</code>. This can be quite useful and elegant (see [http://archive.fo/dUbHK example]).</li> |
| − | <li>The type < |
+ | <li>The type <code>Ordering = LT | EQ | GT</code> is a <code>Monoid</code>, defined in such a way that <code>mconcat (zipWith compare xs ys)</code> computes the lexicographic ordering of <code>xs</code> and <code>ys</code> (if <code>xs</code> and <code>ys</code> have the same length). In particular, <code>mempty = EQ</code>, and <code>mappend</code> evaluates to its leftmost non-<code>EQ</code> argument (or <code>EQ</code> if both arguments are <code>EQ</code>). This can be used together with the function instance of <code>Monoid</code> to do some clever things ([http://www.reddit.com/r/programming/comments/7cf4r/monoids_in_my_programming_language/c06adnx example]).</li> |
| − | <li>There are also < |
+ | <li>There are also <code>Monoid</code> instances for several standard data structures in the containers library ([http://hackage.haskell.org/packages/archive/containers/0.2.0.0/doc/html/index.html haddock]), including <code>Map</code>, <code>Set</code>, and <code>Sequence</code>.</li> |
</ul> |
</ul> |
||
| − | < |
+ | <code>Monoid</code> is also used to enable several other type class instances. |
| − | As noted previously, we can use < |
+ | As noted previously, we can use <code>Monoid</code> to make <code>((,) e)</code> an instance of <code>Applicative</code>: |
<haskell> |
<haskell> |
||
instance Monoid e => Applicative ((,) e) where |
instance Monoid e => Applicative ((,) e) where |
||
| + | pure :: Monoid e => a -> (e,a) |
||
pure x = (mempty, x) |
pure x = (mempty, x) |
||
| + | |||
| + | (<*>) :: Monoid e => (e,a -> b) -> (e,a) -> (e,b) |
||
(u, f) <*> (v, x) = (u `mappend` v, f x) |
(u, f) <*> (v, x) = (u `mappend` v, f x) |
||
</haskell> |
</haskell> |
||
| − | < |
+ | <code>Monoid</code> can be similarly used to make <code>((,) e)</code> an instance of <code>Monad</code> as well; this is known as the ''writer monad''. As we’ve already seen, <code>Writer</code> and <code>WriterT</code> are a newtype wrapper and transformer for this monad, respectively. |
| − | < |
+ | <code>Monoid</code> also plays a key role in the <code>Foldable</code> type class (see section [[#Foldable|Foldable]]). |
| + | ==Further reading== |
||
| − | ==Other monoidal classes: Alternative, MonadPlus, ArrowPlus== |
||
| + | Monoids got a fair bit of attention in 2009, when |
||
| − | The <hask>Alternative</hask> type class ([http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Applicative.html#g:2 haddock]) |
||
| + | [http://blog.enfranchisedmind.com/2009/01/random-thoughts-on-haskell/ a blog post by Brian Hurt] |
||
| − | is for <hask>Applicative</hask> functors which also have |
||
| + | complained about the fact that the names of many Haskell type classes |
||
| + | (<code>Monoid</code> in particular) are taken from abstract mathematics. This |
||
| + | resulted in [http://archive.fo/hkTOb a long Haskell-cafe thread] |
||
| + | arguing the point and discussing monoids in general. |
||
| + | |||
| + | {{note|May its name live forever.}} |
||
| + | |||
| + | However, this was quickly followed by several blog posts about |
||
| + | <code>Monoid</code> {{noteref}}. First, Dan Piponi |
||
| + | wrote a great introductory post, [http://blog.sigfpe.com/2009/01/haskell-monoids-and-their-uses.html Haskell Monoids and their Uses]. This was quickly followed by |
||
| + | Heinrich Apfelmus’ [http://apfelmus.nfshost.com/monoid-fingertree.html Monoids and Finger Trees], an accessible exposition of |
||
| + | Hinze and Paterson’s [http://www.soi.city.ac.uk/%7Eross/papers/FingerTree.html classic paper on 2-3 finger trees], which makes very clever |
||
| + | use of <code>Monoid</code> to implement an elegant and generic data structure. |
||
| + | Dan Piponi then wrote two fascinating articles about using <code>Monoids</code> |
||
| + | (and finger trees): [http://blog.sigfpe.com/2009/01/fast-incremental-regular-expression.html Fast Incremental Regular Expressions] and [http://blog.sigfpe.com/2009/01/beyond-regular-expressions-more.html Beyond Regular Expressions] |
||
| + | |||
| + | In a similar vein, David Place’s article on improving <code>Data.Map</code> in |
||
| + | order to compute incremental folds (see [http://www.haskell.org/wikiupload/6/6a/TMR-Issue11.pdf the Monad Reader issue 11]) |
||
| + | is also a |
||
| + | good example of using <code>Monoid</code> to generalize a data structure. |
||
| + | |||
| + | Some other interesting examples of <code>Monoid</code> use include [http://www.reddit.com/r/programming/comments/7cf4r/monoids_in_my_programming_language/c06adnx building elegant list sorting combinators], [http://byorgey.wordpress.com/2008/04/17/collecting-unstructured-information-with-the-monoid-of-partial-knowledge/ collecting unstructured information], [http://izbicki.me/blog/gausian-distributions-are-monoids combining probability distributions], and a brilliant series of posts by Chung-Chieh Shan and Dylan Thurston using <code>Monoid</code>s to [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers1/ elegantly solve a difficult combinatorial puzzle] (followed by [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers2/ part 2], [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers3/ part 3], [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers4/ part 4]). |
||
| + | |||
| + | As unlikely as it sounds, monads can actually be viewed as a sort of |
||
| + | monoid, with <code>join</code> playing the role of the binary operation and |
||
| + | <code>return</code> the role of the identity; see [http://blog.sigfpe.com/2008/11/from-monoids-to-monads.html Dan Piponi’s blog post]. |
||
| + | |||
| + | =Failure and choice: Alternative, MonadPlus, ArrowPlus= |
||
| + | |||
| + | Several classes (<code>Applicative</code>, <code>Monad</code>, <code>Arrow</code>) have "monoidal" subclasses, intended to model computations that support "failure" and "choice" (in some appropriate sense). |
||
| + | |||
| + | ==Definition== |
||
| + | |||
| + | The <code>Alternative</code> type class ([{{HackageDocs|base|Control-Applicative}}#g:2 haddock]) |
||
| + | is for <code>Applicative</code> functors which also have |
||
a monoid structure: |
a monoid structure: |
||
| Line 688: | Line 1,117: | ||
empty :: f a |
empty :: f a |
||
(<|>) :: f a -> f a -> f a |
(<|>) :: f a -> f a -> f a |
||
| + | |||
| + | some :: f a -> f [a] |
||
| + | many :: f a -> f [a] |
||
</haskell> |
</haskell> |
||
| + | The basic intuition is that <code>empty</code> represents some sort of "failure", and <code>(<|>)</code> represents a choice between alternatives. (However, this intuition does not fully capture the nuance possible; see the section on Laws below.) Of course, <code>(<|>)</code> should be associative and <code>empty</code> should be the identity element for it. |
||
| − | Of course, instances of <hask>Alternative</hask> should satisfy the monoid laws. |
||
| + | Instances of <code>Alternative</code> must implement <code>empty</code> and <code>(<|>)</code>; <code>some</code> and <code>many</code> have default implementations but are included in the class since specialized implementations may be more efficient than the default. |
||
| + | The default definitions of <code>some</code> and <code>many</code> are essentially given by |
||
| − | Likewise, <hask>MonadPlus</hask> ([http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Monad.html#t:MonadPlus haddock]) |
||
| + | |||
| − | is for <hask>Monad</hask>s with a monoid structure: |
||
| + | <haskell> |
||
| + | some v = (:) <$> v <*> many v |
||
| + | many v = some v <|> pure [] |
||
| + | </haskell> |
||
| + | |||
| + | (though for some reason, in actual fact they are not defined via mutual recursion). The intuition is that both keep running <code>v</code>, collecting its results into a list, until it fails; <code>some v</code> requires <code>v</code> to succeed at least once, whereas <code>many v</code> does not require it to succeed at all. That is, <code>many</code> represents 0 or more repetitions of <code>v</code>, whereas <code>some</code> represents 1 or more repetitions. Note that <code>some</code> and <code>many</code> do not make sense for all instances of <code>Alternative</code>; they are discussed further below. |
||
| + | |||
| + | Likewise, <code>MonadPlus</code> ([{{HackageDocs|base|Control-Monad}}#t:MonadPlus haddock]) |
||
| + | is for <code>Monad</code>s with a monoid structure: |
||
<haskell> |
<haskell> |
||
| Line 701: | Line 1,143: | ||
</haskell> |
</haskell> |
||
| + | Finally, <code>ArrowZero</code> and <code>ArrowPlus</code> ([{{HackageDocs|base|Control-Arrow}}#t:ArrowZero haddock]) |
||
| − | The <hask>MonadPlus</hask> documentation states that it is intended to model |
||
| + | represent <code>Arrow</code>s ([[#Arrow|see below]]) with a |
||
| − | monads which also support “choice and failure”; in addition to the |
||
| + | monoid structure: |
||
| − | monoid laws, instances of <hask>MonadPlus</hask> are expected to satisfy |
||
<haskell> |
<haskell> |
||
| + | class Arrow arr => ArrowZero arr where |
||
| − | mzero >>= f = mzero |
||
| + | zeroArrow :: b `arr` c |
||
| − | v >> mzero = mzero |
||
| + | |||
| + | class ArrowZero arr => ArrowPlus arr where |
||
| + | (<+>) :: (b `arr` c) -> (b `arr` c) -> (b `arr` c) |
||
</haskell> |
</haskell> |
||
| + | ==Instances== |
||
| − | which explains the sense in which <hask>mzero</hask> denotes failure. Since |
||
| − | <hask>mzero</hask> should be the identity for <hask>mplus</hask>, the computation <hask>m1 `mplus` m2</hask> succeeds (evaluates to something other than <hask>mzero</hask>) if |
||
| − | either <hask>m1</hask> or <hask>m2</hask> does; so <hask>mplus</hask> represents choice. The <hask>guard</hask> |
||
| − | function can also be used with instances of <hask>MonadPlus</hask>; it requires a |
||
| − | condition to be satisfied and fails (using <hask>mzero</hask>) if it is not. A |
||
| − | simple example of a <hask>MonadPlus</hask> instance is <hask>[]</hask>, which is exactly the |
||
| − | same as the <hask>Monoid</hask> instance for <hask>[]</hask>: the empty list represents |
||
| − | failure, and list concatenation represents choice. In general, |
||
| − | however, a <hask>MonadPlus</hask> instance for a type need not be the same as its |
||
| − | <hask>Monoid</hask> instance; <hask>Maybe</hask> is an example of such a type. A great |
||
| − | introduction to the <hask>MonadPlus</hask> type class, with interesting examples |
||
| − | of its use, is Doug Auclair’s ''MonadPlus: What a Super Monad!'' in [http://www.haskell.org/wikiupload/6/6a/TMR-Issue11.pdf the Monad.Reader issue 11]. |
||
| + | Although this document typically discusses laws before presenting example instances, for <code>Alternative</code> and friends it is worth doing things the other way around, because there is some controversy over the laws and it helps to have some concrete examples in mind when discussing them. We mostly focus on <code>Alternative</code> in this section and the next; now that <code>Applicative</code> is a superclass of <code>Monad</code>, there is little reason to use <code>MonadPlus</code> any longer, and <code>ArrowPlus</code> is rather obscure. |
||
| − | There used to be a type class called <hask>MonadZero</hask> containing only |
||
| − | <hask>mzero</hask>, representing monads with failure. The <hask>do</hask>-notation requires |
||
| − | some notion of failure to deal with failing pattern matches. |
||
| − | Unfortunately, <hask>MonadZero</hask> was scrapped in favor of adding the <hask>fail</hask> |
||
| − | method to the <hask>Monad</hask> class. If we are lucky, someday <hask>MonadZero</hask> will |
||
| − | be restored, and <hask>fail</hask> will be banished to the bit bucket where it |
||
| − | belongs (see [[MonadPlus reform proposal]]). The idea is that any |
||
| − | <hask>do</hask>-block which uses pattern matching (and hence may fail) would require |
||
| − | a <hask>MonadZero</hask> constraint; otherwise, only a <hask>Monad</hask> constraint would be |
||
| − | required. |
||
| + | * <code>Maybe</code> is an instance of <code>Alternative</code>, where <code>empty</code> is <code>Nothing</code> and the choice operator <code>(<|>)</code> results in its first argument when it is <code>Just</code>, and otherwise results in its second argument. Hence folding over a list of <code>Maybe</code> with <code>(<|>)</code> (which can be done with <code>asum</code> from <code>Data.Foldable</code>) results in the first non-<code>Nothing</code> value in the list (or <code>Nothing</code> if there are none). |
||
| − | Finally, <hask>ArrowZero</hask> and <hask>ArrowPlus</hask> ([http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Arrow.html#t:ArrowZero haddock]) |
||
| + | |||
| − | represent <hask>Arrow</hask>s ([[#Arrow|see below]]) with a |
||
| + | * <code>[]</code> is an instance, with <code>empty</code> given by the empty list, and <code>(<|>)</code> equal to <code>(++)</code>. It is worth pointing out that this is identical to the <code>Monoid</code> instance for <code>[a]</code>, whereas the <code>Alternative</code> and <code>Monoid</code> instances for <code>Maybe</code> are different: the <code>Monoid</code> instance for <code>Maybe a</code> requires a <code>Monoid</code> instance for <code>a</code>, and monoidally combines the contained values when presented with two <code>Just</code>s. |
||
| − | monoid structure: |
||
| + | |||
| + | Let's think about the behavior of <code>some</code> and <code>many</code> for <code>Maybe</code> and <code>[]</code>. For <code>Maybe</code>, we have <code>some Nothing = (:) <$> Nothing <*> many Nothing = Nothing <*> many Nothing = Nothing</code>. Hence we also have <code>many Nothing = some Nothing <|> pure [] = Nothing <|> pure [] = pure [] = Just []</code>. Boring. But what about applying <code>some</code> and <code>many</code> to <code>Just</code>? In fact, <code>some (Just a)</code> and <code>many (Just a)</code> are both bottom! The problem is that since <code>Just a</code> is always "successful", the recursion will never terminate. In theory the result "should be" the infinite list <code>[a,a,a,...]</code> but it cannot even start producing any elements of this list, because there is no way for the <code>(<*>)</code> operator to yield any output until it knows that the result of the call to <code>many</code> will be <code>Just</code>. |
||
| + | |||
| + | You can work out the behavior for <code>[]</code> yourself, but it ends up being quite similar: <code>some</code> and <code>many</code> yield boring results when applied to the empty list, and yield bottom when applied to any non-empty list. |
||
| + | |||
| + | In the end, <code>some</code> and <code>many</code> really only make sense when used with some sort of "stateful" <code>Applicative</code> instance, for which an action <code>v</code>, when run multiple times, can succeed some finite number of times and then fail. For example, parsers have this behavior, and indeed, parsers were the original motivating example for the <code>some</code> and <code>many</code> methods; more on this below. |
||
| + | |||
| + | * Since GHC 8.0 (that is, <code>base-4.9</code>), there is an instance of <code>Alternative</code> for <code>IO</code>. <code>empty</code> throws an I/O exception, and <code>(<|>)</code> works by first running its left-hand argument; if the left-hand argument throws an I/O exception, <code>(<|>)</code> catches the exception and then calls its second argument. (Note that other types of exceptions are not caught.) There are other, much better ways to handle I/O errors, but this is a quick and dirty way that may work for simple, one-off programs, such as expressions typed at the GHCi prompt. For example, if you want to read the contents of a file but use some default contents in case the file does not exist, you can just write <code>readFile "somefile.txt" <|> return "default file contents"</code>. |
||
| + | |||
| + | * <code>Concurrently</code> from the <code>async</code> package has an <code>Alternative</code> instance, for which <code>c1 <|> c2</code> races <code>c1</code> and <code>c2</code> in parallel, and returns the result of whichever finishes first. <code>empty</code> corresponds to the action that runs forever without returning a value. |
||
| + | |||
| + | * Practically any parser type (e.g. from <code>parsec</code>, <code>megaparsec</code>, <code>trifecta</code>, ...) has an <code>Alternative</code> instance, where <code>empty</code> is an unconditional parse failure, and <code>(<|>)</code> is left-biased choice. That is, <code>p1 <|> p2</code> first tries parsing with <code>p1</code>, and if <code>p1</code> fails then it tries <code>p2</code> instead. |
||
| + | |||
| + | <code>some</code> and <code>many</code> work particularly well with parser types having an <code>Applicative</code> instance: if <code>p</code> is a parser, then <code>some p</code> parses one or more consecutive occurrences of <code>p</code> (i.e. it will parse as many occurrences of <code>p</code> as possible and then stop), and <code>many p</code> parses zero or more occurrences. |
||
| + | |||
| + | ==Laws== |
||
| + | |||
| + | Of course, instances of <code>Alternative</code> should satisfy the monoid laws |
||
<haskell> |
<haskell> |
||
| + | empty <|> x = x |
||
| − | class Arrow (~>) => ArrowZero (~>) where |
||
| + | x <|> empty = x |
||
| − | zeroArrow :: b ~> c |
||
| + | (x <|> y) <|> z = x <|> (y <|> z) |
||
| + | </haskell> |
||
| + | The documentation for <code>some</code> and <code>many</code> states that they should be the "least solution" (i.e. least in the definedness partial order) to their characterizing, mutually recursive default definitions. However, [https://www.reddit.com/r/haskell/comments/2j8bvl/laws_of_some_and_many/ this is controversial], and probably wasn't really thought out very carefully. |
||
| − | class ArrowZero (~>) => ArrowPlus (~>) where |
||
| + | |||
| − | (<+>) :: (b ~> c) -> (b ~> c) -> (b ~> c) |
||
| + | Since <code>Alternative</code> is a subclass of <code>Applicative</code>, a natural question is, "how should <code>empty</code> and <code>(<|>)</code> interact with <code>(<*>)</code> and <code>pure</code>?" |
||
| + | |||
| + | Almost everyone agrees on the ''left zero'' law (though see the discussion of the ''right zero'' law below): |
||
| + | |||
| + | <haskell> |
||
| + | empty <*> f = empty |
||
</haskell> |
</haskell> |
||
| + | After this is where it starts to get a bit hairy though. It turns out there are several other laws one might imagine adding, and different instances satisfy different laws. |
||
| − | ==Further reading== |
||
| + | * ''Right Zero'':<p>Another obvious law would be <haskell>f <*> empty = empty</haskell></p><p>This law is satisfied by most instances; however, it is not satisfied by <code>IO</code>. Once the effects in <code>f</code> have been executed, there is no way to roll them back if we later encounter an exception. Now consider the <code>Backwards</code> applicative transformer from the <code>transformers</code> package. If <code>f</code> is <code>Applicative</code>, then so is <code>Backwards f</code>; it works the same way but performs the actions of the arguments to <code>(<*>)</code> in the reverse order. There is also an instance <code>Alternative f => Alternative (Backwards f)</code>. If some <code>f</code> (such as <code>IO</code>) satisfies ''left zero'' but not ''right zero'', then <code>Backwards f</code> satisfies ''right zero'' but not ''left zero''! So even the ''left zero'' law is suspect. The point is that given the existence of <code>Backwards</code> we cannot privilege one direction or the other.</p> |
||
| − | Monoids have gotten a fair bit of attention recently, ultimately due |
||
| − | to |
||
| − | [http://enfranchisedmind.com/blog/posts/random-thoughts-on-haskell/ a blog post by Brian Hurt], in which he |
||
| − | complained about the fact that the names of many Haskell type classes |
||
| − | (<hask>Monoid</hask> in particular) are taken from abstract mathematics. This |
||
| − | resulted in [http://thread.gmane.org/gmane.comp.lang.haskell.cafe/50590 a long haskell-cafe thread] |
||
| − | arguing the point and discussing monoids in general. |
||
| − | {{note|May its name live forever.}} |
||
| + | * ''Left Distribution'':<p><haskell>(a <|> b) <*> c = (a <*> c) <|> (b <*> c)</haskell></p><p>This distributivity law is satisfied by <code>[]</code> and <code>Maybe</code>, as you may verify. However, it is ''not'' satisfied by <code>IO</code> or most parsers. The reason is that <code>a</code> and <code>b</code> can have effects which influence execution of <code>c</code>, and the left-hand side may end up failing where the right-hand side succeeds.</p><p>For example, consider <code>IO</code>, and suppose that <code>a</code> always executes successfully, but <code>c</code> throws an I/O exception after <code>a</code> has run. Concretely, say, <code>a</code> might ensure that a certain file does not exist (deleting it if it does exist or doing nothing if it does not), and then <code>c</code> tries to read that file. In that case <code>(a <|> b) <*> c</code> will first delete the file, ignoring <code>b</code> since <code>a</code> is successful, and then throw an exception when <code>c</code> tries to read the file. On the other hand, <code>b</code> might ensure that the same file in question ''does'' exist. In that case <code>(a <*> c) <|> (b <*> c)</code> would succeed: after <code>(a <*> c)</code> throws an exception, it would be caught by <code>(<|>)</code>, and then <code>(b <*> c)</code> would be tried.</p><p>This law does not hold for parsers for a similar reason: <code>(a <|> b) <*> c</code> has to "commit" to parsing with <code>a</code> or <code>b</code> before running <code>c</code>, whereas <code>(a <*> c) <|> (b <*> c)</code> allows backtracking if <code>a <*> c</code> fails. In the particular case that <code>a</code> succeeds but <code>c</code> fails after <code>a</code> but not after <code>b</code>, these may give different results. For example, suppose <code>a</code> and <code>c</code> both expect to see two asterisks, but <code>b</code> expects to see only one. If there are only three asterisks in the input, <code>b <*> c</code> will be successful whereas <code>a <*> c</code> will not.</p> |
||
| − | However, this was quickly followed by several blog posts about |
||
| − | <hask>Monoid</hask> {{noteref}}. First, Dan Piponi |
||
| − | wrote a great introductory post, [http://blog.sigfpe.com/2009/01/haskell-monoids-and-their-uses.html Haskell Monoids and their Uses]. This was quickly followed by |
||
| − | Heinrich Apfelmus’s [http://apfelmus.nfshost.com/monoid-fingertree.html Monoids and Finger Trees], an accessible exposition of |
||
| − | Hinze and Paterson’s [http://www.soi.city.ac.uk/%7Eross/papers/FingerTree.html classic paper on 2-3 finger trees], which makes very clever |
||
| − | use of <hask>Monoid</hask> to implement an elegant and generic data structure. |
||
| − | Dan Piponi then wrote two fascinating articles about using <hask>Monoids</hask> |
||
| − | (and finger trees): [http://blog.sigfpe.com/2009/01/fast-incremental-regular-expression.html Fast Incremental Regular Expressions] and [http://blog.sigfpe.com/2009/01/beyond-regular-expressions-more.html Beyond Regular Expressions] |
||
| + | * ''Right Distribution'':<p><haskell>a <*> (b <|> c) = (a <*> b) <|> (a <*> c)</haskell></p><p>This law is not satisfied by very many instances, but it's still worth discussing. In particular the law is still satisfied by <code>Maybe</code>. However, it is ''not'' satisfied by, for example, lists. The problem is that the results come out in a different order. For example, suppose <code>a = [(+1), (*10)]</code>, <code>b = [2]</code>, and <code>c = [3]</code>. Then the left-hand side yields <code>[3,4,20,30]</code>, whereas the right-hand side is <code>[3,20,4,30]</code>.</p><p><code>IO</code> does not satisfy it either, since, for example, <code>a</code> may succeed only the ''second'' time it is executed. Parsers, on the other hand, may or may not satisfy this law, depending on how they handle backtracking. Parsers for which <code>(<|>)</code> by itself does full backtracking will satisfy the law; but for many parser combinator libraries this is not the case, for efficiency reasons. For example, parsec fails this law: if <code>a</code> succeeds while consuming some input, and afterwards <code>b</code> fails without consuming any input, then the left-hand side may succeed while the right-hand side fails: after <code>(a <*> b)</code> fails, the right-hand side tries to re-run <code>a</code> without backtracking over the input the original <code>a</code> consumed.</p> |
||
| − | In a similar vein, David Place’s article on improving <hask>Data.Map</hask> in |
||
| − | order to compute incremental folds (see [http://www.haskell.org/sitewiki/images/6/6a/TMR-Issue11.pdf the Monad Reader issue 11]) |
||
| − | is also a |
||
| − | good example of using <hask>Monoid</hask> to generalize a data structure. |
||
| + | * ''Left Catch'':<p><haskell>(pure a) <|> x = pure a</haskell></p><p>Intuitively, this law states that <code>pure</code> should always represent a "successful" computation. It is satisfied by <code>Maybe</code>, <code>IO</code>, and parsers. However, it is not satisfied by lists, since lists collect ''all'' possible results: it corresponds to <code>[a] ++ x == [a]</code> which is obviously false.</p> |
||
| − | Some other interesting examples of <hask>Monoid</hask> use include [http://www.reddit.com/r/programming/comments/7cf4r/monoids_in_my_programming_language/c06adnx building elegant list sorting combinators], |
||
| − | [http://byorgey.wordpress.com/2008/04/17/collecting-unstructured-information-with-the-monoid-of-partial-knowledge/ collecting unstructured information], |
||
| − | and a brilliant series of posts by Chung-Chieh Shan and Dylan Thurston |
||
| − | using <hask>Monoid</hask>s to [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers1/ elegantly solve a difficult combinatorial puzzle] (followed by |
||
| − | [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers2/ part 2], |
||
| − | [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers3/ part 3], |
||
| − | [http://conway.rutgers.edu/~ccshan/wiki/blog/posts/WordNumbers4/ part 4]). |
||
| + | This, then, is the situation: we have a lot of instances of <code>Alternative</code> (and <code>MonadPlus</code>), with each instance satisfying some ''subset'' of these laws. Moreover, it's not always the ''same'' subset, so there is no obvious "default" set of laws to choose. For now at least, we just have to live with the situation. When using a particular instance of <code>Alternative</code> or <code>MonadPlus</code>, it's worth thinking carefully about which laws it satisfies. |
||
| − | As unlikely as it sounds, monads can actually be viewed as a sort of |
||
| + | |||
| − | monoid, with <hask>join</hask> playing the role of the binary operation and |
||
| + | ==Utility functions== |
||
| − | <hask>return</hask> the role of the identity; see [http://blog.sigfpe.com/2008/11/from-monoids-to-monads.html Dan Piponi’s blog post]. |
||
| + | |||
| + | There are a few <code>Alternative</code>-specific utility functions worth mentioning: |
||
| + | |||
| + | * <haskell>guard :: Alternative f => Bool -> f ()</haskell> checks the given condition, and evaluates to <code>pure ()</code> if the condition holds, and <code>empty</code> if not. This can be used to create a conditional failure point in the middle of a computation, where the computation only proceeds if a certain condition holds. |
||
| + | |||
| + | * <haskell>optional :: Alternative f => f a -> f (Maybe a)</haskell> reifies potential failure into the <code>Maybe</code> type: that is, <code>optional x</code> is a computation which always succeeds, returning <code>Nothing</code> if <code>x</code> fails and <code>Just a</code> if <code>x</code> successfully results in <code>a</code>. It is useful, for example, in the context of parsers, where it corresponds to a production which can occur zero or one times. |
||
| + | |||
| + | ==Further reading== |
||
| + | |||
| + | There used to be a type class called <code>MonadZero</code> containing only |
||
| + | <code>mzero</code>, representing monads with failure. The <code>do</code>-notation requires |
||
| + | some notion of failure to deal with failing pattern matches. |
||
| + | Unfortunately, <code>MonadZero</code> was scrapped in favor of adding the <code>fail</code> |
||
| + | method to the <code>Monad</code> class. If we are lucky, someday <code>MonadZero</code> will |
||
| + | be restored, and <code>fail</code> will be banished to the bit bucket where it |
||
| + | belongs (see [[MonadPlus reform proposal]]). The idea is that any |
||
| + | <code>do</code>-block which uses pattern matching (and hence may fail) would require |
||
| + | a <code>MonadZero</code> constraint; otherwise, only a <code>Monad</code> constraint would be |
||
| + | required. |
||
| + | |||
| + | A great introduction to the <code>MonadPlus</code> type class, with interesting examples of its use, is Doug Auclair’s ''MonadPlus: What a Super Monad!'' in [http://www.haskell.org/wikiupload/6/6a/TMR-Issue11.pdf the Monad.Reader issue 11]. |
||
| + | |||
| + | Another interesting use of <code>MonadPlus</code> can be found in Christiansen et al, [http://www-ps.informatik.uni-kiel.de/~sad/icfp2016-preprint.pdf All Sorts of Permutations], from ICFP 2016. |
||
| + | |||
| + | The [https://hackage.haskell.org/package/logict logict package] defines a type with prominent <code>Alternative</code> and <code>MonadPlus</code> instances that can be used to efficiently enumerate possibilities subject to constraints, ''i.e.'' logic programming; it's like the list monad on steroids. |
||
=Foldable= |
=Foldable= |
||
| − | The < |
+ | The <code>Foldable</code> class, defined in the <code>Data.Foldable</code> |
| − | module ([ |
+ | module ([{{HackageDocs|base|Data-Foldable}} haddock]), abstracts over containers which can be |
“folded” into a summary value. This allows such folding operations |
“folded” into a summary value. This allows such folding operations |
||
to be written in a container-agnostic way. |
to be written in a container-agnostic way. |
||
| Line 793: | Line 1,246: | ||
==Definition== |
==Definition== |
||
| − | The definition of the < |
+ | The definition of the <code>Foldable</code> type class is: |
<haskell> |
<haskell> |
||
| Line 799: | Line 1,252: | ||
fold :: Monoid m => t m -> m |
fold :: Monoid m => t m -> m |
||
foldMap :: Monoid m => (a -> m) -> t a -> m |
foldMap :: Monoid m => (a -> m) -> t a -> m |
||
| − | |||
foldr :: (a -> b -> b) -> b -> t a -> b |
foldr :: (a -> b -> b) -> b -> t a -> b |
||
| − | + | foldr' :: (a -> b -> b) -> b -> t a -> b |
|
| + | foldl :: (b -> a -> b) -> b -> t a -> b |
||
| + | foldl' :: (b -> a -> b) -> b -> t a -> b |
||
foldr1 :: (a -> a -> a) -> t a -> a |
foldr1 :: (a -> a -> a) -> t a -> a |
||
foldl1 :: (a -> a -> a) -> t a -> a |
foldl1 :: (a -> a -> a) -> t a -> a |
||
| + | toList :: t a -> [a] |
||
| + | null :: t a -> Bool |
||
| + | length :: t a -> Int |
||
| + | elem :: Eq a => a -> t a -> Bool |
||
| + | maximum :: Ord a => t a -> a |
||
| + | minimum :: Ord a => t a -> a |
||
| + | sum :: Num a => t a -> a |
||
| + | product :: Num a => t a -> a |
||
</haskell> |
</haskell> |
||
| − | This may look complicated, but in fact, to make a < |
+ | This may look complicated, but in fact, to make a <code>Foldable</code> instance |
| − | you only need to implement one method: your choice of < |
+ | you only need to implement one method: your choice of <code>foldMap</code> or |
| − | < |
+ | <code>foldr</code>. All the other methods have default implementations in terms |
| − | of these, and are |
+ | of these, and are included in the class in case more |
efficient implementations can be provided. |
efficient implementations can be provided. |
||
==Instances and examples== |
==Instances and examples== |
||
| − | The type of < |
+ | The type of <code>foldMap</code> should make it clear what it is supposed to do: |
| − | given a way to convert the data in a container into a < |
+ | given a way to convert the data in a container into a <code>Monoid</code> (a |
| − | function < |
+ | function <code>a -> m</code>) and a container of <code>a</code>’s (<code>t a</code>), <code>foldMap</code> |
provides a way to iterate over the entire contents of the container, |
provides a way to iterate over the entire contents of the container, |
||
| − | converting all the < |
+ | converting all the <code>a</code>’s to <code>m</code>’s and combining all the <code>m</code>’s with |
| − | < |
+ | <code>mappend</code>. The following code shows two examples: a simple |
| − | implementation of < |
+ | implementation of <code>foldMap</code> for lists, and a binary tree example |
| − | provided by the < |
+ | provided by the <code>Foldable</code> documentation. |
<haskell> |
<haskell> |
||
instance Foldable [] where |
instance Foldable [] where |
||
| + | foldMap :: Monoid m => (a -> m) -> [a] -> m |
||
foldMap g = mconcat . map g |
foldMap g = mconcat . map g |
||
| Line 830: | Line 1,293: | ||
instance Foldable Tree where |
instance Foldable Tree where |
||
| − | foldMap |
+ | foldMap :: Monoid m => (a -> m) -> Tree a -> m |
| − | foldMap f |
+ | foldMap f Empty = mempty |
| − | foldMap f ( |
+ | foldMap f (Leaf x) = f x |
| − | + | foldMap f (Node l k r) = foldMap f l `mappend` f k `mappend` foldMap f r |
|
</haskell> |
</haskell> |
||
| − | The < |
+ | The <code>Foldable</code> module also provides instances for <code>Maybe</code> and <code>Array</code>; |
| + | additionally, many of the data structures found in the standard [http://hackage.haskell.org/package/containers containers library] (for example, <code>Map</code>, <code>Set</code>, <code>Tree</code>, |
||
| − | more general, since the <hask>foldr</hask> in the <hask>Prelude</hask> works only on lists. |
||
| + | and <code>Sequence</code>) provide their own <code>Foldable</code> instances. |
||
| + | {{Exercises| |
||
| − | The <hask>Foldable</hask> module also provides instances for <hask>Maybe</hask> and <hask>Array</hask>; |
||
| + | # Implement <code>fold</code> in terms of <code>foldMap</code>. |
||
| − | additionally, many of the data structures found in the standard [http://hackage.haskell.org/package/containers containers library] (for example, <hask>Map</hask>, <hask>Set</hask>, <hask>Tree</hask>, |
||
| + | # What would you need in order to implement <code>foldMap</code> in terms of <code>fold</code>? |
||
| − | and <hask>Sequence</hask>) provide their own <hask>Foldable</hask> instances. |
||
| + | # Implement <code>foldMap</code> in terms of <code>foldr</code>. |
||
| + | # Implement <code>foldr</code> in terms of <code>foldMap</code> (hint: use the <code>Endo</code> monoid). |
||
| + | # What is the type of <code>foldMap . foldMap</code>? Or <code>foldMap . foldMap . foldMap</code>, etc.? What do they do? |
||
| + | }} |
||
==Derived folds== |
==Derived folds== |
||
| − | Given an instance of < |
+ | Given an instance of <code>Foldable</code>, we can write generic, |
container-agnostic functions such as: |
container-agnostic functions such as: |
||
| Line 863: | Line 1,331: | ||
</haskell> |
</haskell> |
||
| − | The < |
+ | The <code>Foldable</code> module also provides a large number of predefined |
| − | folds |
+ | folds. These used to be generalized versions of <code>Prelude</code> functions of the |
| − | same name that only |
+ | same name that only worked on lists; but [https://wiki.haskell.org/Foldable_Traversable_In_Prelude as of GHC 7.10], the generalized versions themselves are now exported from the Prelude: for example, <code>concat</code>, <code>concatMap</code>, <code>and</code>, |
| − | < |
+ | <code>or</code>, <code>any</code>, <code>all</code>, <code>sum</code>, <code>product</code>, <code>maximum</code>(<code>By</code>), |
| + | <code>minimum</code>(<code>By</code>), <code>elem</code>, <code>notElem</code>, and <code>find</code>. For example, before GHC 7.10, <code>length</code> used to have type <code>length :: [a] -> Int</code>; now it has type <code>Foldable t => t a -> Int</code> (and is in fact the same as the <code>containerSize</code> function shown above). |
||
| − | <hask>minimum</hask>(<hask>By</hask>), <hask>elem</hask>, <hask>notElem</hask>, and <hask>find</hask>. The reader may enjoy |
||
| − | coming up with elegant implementations of these functions using <hask>fold</hask> |
||
| − | or <hask>foldMap</hask> and appropriate <hask>Monoid</hask> instances. |
||
| + | The important function <code>toList</code> is also provided, which turns any <code>Foldable</code> structure into a list of its elements in left-right order; it works by folding with the list monoid. |
||
| − | There are also generic functions that work with <hask>Applicative</hask> or |
||
| + | |||
| − | <hask>Monad</hask> instances to generate some sort of computation from each |
||
| + | There are also generic functions that work with <code>Applicative</code> or |
||
| + | <code>Monad</code> instances to generate some sort of computation from each |
||
element in a container, and then perform all the side effects from |
element in a container, and then perform all the side effects from |
||
| − | those computations, discarding the results: < |
+ | those computations, discarding the results: <code>traverse_</code>, <code>sequenceA_</code>, |
| − | and others. The results must be discarded because the < |
+ | and others. The results must be discarded because the <code>Foldable</code> |
class is too weak to specify what to do with them: we cannot, in |
class is too weak to specify what to do with them: we cannot, in |
||
| − | general, make an arbitrary < |
+ | general, make an arbitrary <code>Applicative</code> or <code>Monad</code> instance into a <code>Monoid</code>, but we can make <code>m ()</code> into a <code>Monoid</code> for any such <code>m</code>. If we do have an <code>Applicative</code> or <code>Monad</code> with a monoid |
| + | structure—that is, an <code>Alternative</code> or a <code>MonadPlus</code>—then we can |
||
| − | <hask>Monoid</hask>. If we do have an <hask>Applicative</hask> or <hask>Monad</hask> with a monoid |
||
| + | use the <code>asum</code> or <code>msum</code> functions, which can combine the results as |
||
| − | structure—that is, an <hask>Alternative</hask> or a <hask>MonadPlus</hask>—then we can |
||
| + | well. Consult the [{{HackageDocs|base|Data-Foldable}} <code>Foldable</code> documentation] for |
||
| − | use the <hask>asum</hask> or <hask>msum</hask> functions, which can combine the results as |
||
| − | well. Consult the [http://haskell.org/ghc/docs/latest/html/libraries/base/Data-Foldable.html <hask>Foldable</hask> documentation] for |
||
more details on any of these functions. |
more details on any of these functions. |
||
| − | Note that the < |
+ | Note that the <code>Foldable</code> operations always forget the structure of |
| − | the container being folded. If we start with a container of type < |
+ | the container being folded. If we start with a container of type <code>t a</code> for some <code>Foldable t</code>, then <code>t</code> will never appear in the output |
| − | type of any operations defined in the < |
+ | type of any operations defined in the <code>Foldable</code> module. Many times |
this is exactly what we want, but sometimes we would like to be able |
this is exactly what we want, but sometimes we would like to be able |
||
to generically traverse a container while preserving its |
to generically traverse a container while preserving its |
||
| − | structure—and this is exactly what the < |
+ | structure—and this is exactly what the <code>Traversable</code> class provides, |
which will be discussed in the next section. |
which will be discussed in the next section. |
||
| + | |||
| + | {{Exercises| |
||
| + | # Implement <code>toList :: Foldable f {{=}}> f a -> [a]</code> in terms of either <code>foldr</code> or <code>foldMap</code>. |
||
| + | # Show how one could implement the generic version of <code>foldr</code> in terms of <code>toList</code>, assuming we had only the list-specific <code>foldr :: (a -> b -> b) -> b -> [a] -> b</code>. |
||
| + | # Pick some of the following functions to implement: <code>concat</code>, <code>concatMap</code>, <code>and</code>, <code>or</code>, <code>any</code>, <code>all</code>, <code>sum</code>, <code>product</code>, <code>maximum</code>(<code>By</code>), <code>minimum</code>(<code>By</code>), <code>elem</code>, <code>notElem</code>, and <code>find</code>. Figure out how they generalize to <code>Foldable</code> and come up with elegant implementations using <code>fold</code> or <code>foldMap</code> along with appropriate <code>Monoid</code> instances. |
||
| + | }} |
||
| + | |||
| + | ==Utility functions== |
||
| + | |||
| + | * <code>asum :: (Alternative f, Foldable t) => t (f a) -> f a</code> takes a container full of computations and combines them using <code>(<|>)</code>. |
||
| + | |||
| + | * <code>sequenceA_ :: (Applicative f, Foldable t) => t (f a) -> f ()</code> takes a container full of computations and runs them in sequence, discarding the results (that is, they are used only for their effects). Since the results are discarded, the container only needs to be <code>Foldable</code>. (Compare with <code>sequenceA :: (Applicative f, Traversable t) => t (f a) -> f (t a)</code>, which requires a stronger <code>Traversable</code> constraint in order to be able to reconstruct a container of results having the same shape as the original container.) |
||
| + | |||
| + | * <code>traverse_ :: (Applicative f, Foldable t) => (a -> f b) -> t a -> f ()</code> applies the given function to each element in a foldable container and sequences the effects (but discards the results). |
||
| + | |||
| + | * <code>for_</code> is the same as <code>traverse_</code> but with its arguments flipped. This is the moral equivalent of a "foreach" loop in an imperative language. |
||
| + | |||
| + | * For historical reasons, there are also variants of all the above with overly-restrictive <code>Monad</code>(-like) constraints: <code>msum</code> is the same as <code>asum</code> specialized to <code>MonadPlus</code>, and <code>sequence_</code>, <code>mapM_</code>, and <code>forM_</code> respectively are <code>Monad</code> specializations of <code>sequenceA_</code>, <code>traverse_</code>, and <code>for_</code>. |
||
| + | |||
| + | {{Exercises| |
||
| + | # Implement <code>traverse_</code> in terms of <code>sequenceA_</code> and vice versa. One of these will need an extra constraint. What is it? |
||
| + | }} |
||
| + | |||
| + | ==Foldable actually isn't== |
||
| + | |||
| + | The generic term "fold" is often used to refer to the more technical concept of [[Catamorphisms|catamorphism]]. Intuitively, given a way to summarize "one level of structure" (where recursive subterms have already been replaced with their summaries), a catamorphism can summarize an entire recursive structure. It is important to realize that <code>Foldable</code> does <i>not</i> correspond to catamorphisms, but to something weaker. In particular, <code>Foldable</code> allows observing only the left-right traversal order of elements within a structure, not the actual structure itself. Put another way, every use of <code>Foldable</code> can be expressed in terms of <code>toList</code>. For example, <code>fold</code> itself is equivalent to <code>mconcat . toList</code>. |
||
| + | |||
| + | This is sufficient for many tasks, but not all. For example, consider trying to compute the depth of a <code>Tree</code>: try as we might, there is no way to implement it using <code>Foldable</code>. However, it <i>can</i> be implemented as a catamorphism. |
||
==Further reading== |
==Further reading== |
||
| − | The < |
+ | The <code>Foldable</code> class had its genesis in [http://www.soi.city.ac.uk/~ross/papers/Applicative.html McBride and Paterson’s paper] |
| − | introducing < |
+ | introducing <code>Applicative</code>, although it has |
been fleshed out quite a bit from the form in the paper. |
been fleshed out quite a bit from the form in the paper. |
||
| − | An interesting use of < |
+ | An interesting use of <code>Foldable</code> (as well as <code>Traversable</code>) can be |
found in Janis Voigtländer’s paper [http://doi.acm.org/10.1145/1480881.1480904 Bidirectionalization for free!]. |
found in Janis Voigtländer’s paper [http://doi.acm.org/10.1145/1480881.1480904 Bidirectionalization for free!]. |
||
| + | |||
| + | For more on the relationship between <code>fold</code>, <code>foldMap</code>, and <code>foldr</code>, see [https://byorgey.wordpress.com/2012/11/05/foldr-is-made-of-monoids/ foldr is made of monoids]. |
||
| + | |||
| + | There was [http://tojans.me/blog/2015/10/13/foldable-for-non-haskellers-haskells-controversial-ftp-proposal/ quite a bit of controversy] in the Haskell community about a [https://wiki.haskell.org/Foldable_Traversable_In_Prelude proposal to integrate <code>Foldable</code> (and <code>Traversable</code>) more tightly into the Prelude], known as the FTP. Some of the controversy centered around <code>Foldable</code> instances such as the one for <code>((,) a)</code>, which, together with generalized types for functions such as <code>length :: Foldable t => t a -> Int</code>, allow one to derive seemingly nonsensical results such as <code>length (2,3) = 1</code>. Here is a [https://www.youtube.com/watch?v=87re_yIQMDw humorous talk] poking fun at the situation. |
||
=Traversable= |
=Traversable= |
||
| Line 905: | Line 1,404: | ||
==Definition== |
==Definition== |
||
| − | The < |
+ | The <code>Traversable</code> type class, defined in the <code>Data.Traversable</code> |
| − | module ([ |
+ | module ([{{HackageDocs|base|Data-Traversable}} haddock]), is: |
<haskell> |
<haskell> |
||
| Line 912: | Line 1,411: | ||
traverse :: Applicative f => (a -> f b) -> t a -> f (t b) |
traverse :: Applicative f => (a -> f b) -> t a -> f (t b) |
||
sequenceA :: Applicative f => t (f a) -> f (t a) |
sequenceA :: Applicative f => t (f a) -> f (t a) |
||
| − | mapM :: Monad m => (a -> m b) -> t a -> m (t b) |
+ | mapM :: Monad m => (a -> m b) -> t a -> m (t b) |
| − | sequence :: Monad m => t (m a) -> m (t a) |
+ | sequence :: Monad m => t (m a) -> m (t a) |
</haskell> |
</haskell> |
||
| − | As you can see, every < |
+ | As you can see, every <code>Traversable</code> is also a <code>Foldable</code> <code>Functor</code>. To make a <code>Traversable</code> instance, it suffices to implement either <code>traverse</code> or |
| + | <code>sequenceA</code>; the other methods all have default implementations in |
||
| − | <hask>Foldable</hask>, there is a lot in this type class, but making instances is |
||
| + | terms of these. Note that <code>mapM</code> and <code>sequence</code> only exist for historical reasons; especially now that <code>Applicative</code> is a superclass of <code>Monad</code>, they are nothing more than copies of <code>traverse</code> and <code>sequenceA</code>, respectively, but with more restrictive types. |
||
| − | actually rather easy: one need only implement <hask>traverse</hask> or |
||
| − | <hask>sequenceA</hask>; the other methods all have default implementations in |
||
| − | terms of these functions. A good exercise is to figure out what the default |
||
| − | implementations should be: given either <hask>traverse</hask> or <hask>sequenceA</hask>, how |
||
| − | would you define the other three methods? (Hint for <hask>mapM</hask>: |
||
| − | <hask>Control.Applicative</hask> exports the <hask>WrapMonad</hask> newtype, which makes any |
||
| − | <hask>Monad</hask> into an <hask>Applicative</hask>. The <hask>sequence</hask> function can be implemented in terms |
||
| − | of <hask>mapM</hask>.) |
||
==Intuition== |
==Intuition== |
||
| + | |||
| − | The key method of the <hask>Traversable</hask> class, and the source of its |
||
| + | The key method of the <code>Traversable</code> class is <code>traverse</code>, which has the following type: |
||
| − | unique power, is <hask>sequenceA</hask>. Consider its type: |
||
| + | <haskell> |
||
| + | traverse :: Applicative f => (a -> f b) -> t a -> f (t b) |
||
| + | </haskell> |
||
| + | This leads us to view <code>Traversable</code> as a generalization of <code>Functor</code>. <code>traverse</code> is an "effectful <code>fmap</code>": it allows us to map over a structure of type <code>t a</code>, applying a function to every element of type <code>a</code> in order to produce a new structure of type <code>t b</code>; but along the way the function may have some effects (captured by the applicative functor <code>f</code>). |
||
| + | |||
| + | Alternatively, we may consider the <code>sequenceA</code> function. Consider its type: |
||
<haskell> |
<haskell> |
||
sequenceA :: Applicative f => t (f a) -> f (t a) |
sequenceA :: Applicative f => t (f a) -> f (t a) |
||
| Line 936: | Line 1,434: | ||
This answers the fundamental question: when can we commute two |
This answers the fundamental question: when can we commute two |
||
functors? For example, can we turn a tree of lists into a list of |
functors? For example, can we turn a tree of lists into a list of |
||
| + | trees? |
||
| − | trees? (Answer: yes, in two ways. Figuring out what they are, and |
||
| − | why, is left as an exercise. A much more challenging question is |
||
| − | whether a list of trees can be turned into a tree of lists.) |
||
The ability to compose two monads depends crucially on this ability to |
The ability to compose two monads depends crucially on this ability to |
||
commute functors. Intuitively, if we want to build a composed monad |
commute functors. Intuitively, if we want to build a composed monad |
||
| − | < |
+ | <code>M a = m (n a)</code> out of monads <code>m</code> and <code>n</code>, then to be able to |
| − | implement < |
+ | implement <code>join :: M (M a) -> M a</code>, that is, |
| − | < |
+ | <code>join :: m (n (m (n a))) -> m (n a)</code>, we have to be able to commute |
| − | the < |
+ | the <code>n</code> past the <code>m</code> to get <code>m (m (n (n a)))</code>, and then we can use the |
| − | < |
+ | <code>join</code>s for <code>m</code> and <code>n</code> to produce something of type <code>m (n a)</code>. See |
| − | [http://web.cecs.pdx.edu/~mpj/pubs/springschool.html Mark |
+ | [http://web.cecs.pdx.edu/~mpj/pubs/springschool.html Mark Jones’ paper] for more details. |
| + | |||
| + | It turns out that given a <code>Functor</code> constraint on the type <code>t</code>, <code>traverse</code> and <code>sequenceA</code> are equivalent in power: either can be implemented in terms of the other. |
||
| + | |||
| + | {{Exercises| |
||
| + | # There are at least two natural ways to turn a tree of lists into a list of trees. What are they, and why? |
||
| + | # Give a natural way to turn a list of trees into a tree of lists. |
||
| + | # What is the type of <code>traverse . traverse</code>? What does it do? |
||
| + | # Implement <code>traverse</code> in terms of <code>sequenceA</code>, and vice versa. |
||
| + | }} |
||
==Instances and examples== |
==Instances and examples== |
||
| − | What’s an example of a < |
+ | What’s an example of a <code>Traversable</code> instance? |
The following code shows an example instance for the same |
The following code shows an example instance for the same |
||
| − | < |
+ | <code>Tree</code> type used as an example in the previous <code>Foldable</code> section. It |
| − | is instructive to compare this instance with a < |
+ | is instructive to compare this instance with a <code>Functor</code> instance for |
| − | < |
+ | <code>Tree</code>, which is also shown. |
<haskell> |
<haskell> |
||
| Line 961: | Line 1,466: | ||
instance Traversable Tree where |
instance Traversable Tree where |
||
| + | traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b) |
||
traverse g Empty = pure Empty |
traverse g Empty = pure Empty |
||
traverse g (Leaf x) = Leaf <$> g x |
traverse g (Leaf x) = Leaf <$> g x |
||
| Line 968: | Line 1,474: | ||
instance Functor Tree where |
instance Functor Tree where |
||
| + | fmap :: (a -> b) -> Tree a -> Tree b |
||
fmap g Empty = Empty |
fmap g Empty = Empty |
||
fmap g (Leaf x) = Leaf $ g x |
fmap g (Leaf x) = Leaf $ g x |
||
| Line 975: | Line 1,482: | ||
</haskell> |
</haskell> |
||
| − | It should be clear that the < |
+ | It should be clear that the <code>Traversable</code> and <code>Functor</code> instances for |
| − | < |
+ | <code>Tree</code> are structurally identical; the only difference is that the <code>Functor</code> |
instance involves normal function application, whereas the |
instance involves normal function application, whereas the |
||
| − | applications in the < |
+ | applications in the <code>Traversable</code> instance take place within an |
| − | < |
+ | <code>Applicative</code> context, using <code>(<$>)</code> and <code>(<*>)</code>. This same pattern will hold for any type. |
| − | be |
||
| − | true for any type. |
||
| − | Any < |
+ | Any <code>Traversable</code> functor is also <code>Foldable</code>, and a <code>Functor</code>. We can see |
this not only from the class declaration, but by the fact that we can |
this not only from the class declaration, but by the fact that we can |
||
| − | implement the methods of both classes given only the < |
+ | implement the methods of both classes given only the <code>Traversable</code> |
| + | methods. |
||
| − | methods. A good exercise is to implement <hask>fmap</hask> and <hask>foldMap</hask> using |
||
| − | only the <hask>Traversable</hask> methods; the implementations are surprisingly |
||
| − | elegant. The <hask>Traversable</hask> module provides these |
||
| − | implementations as <hask>fmapDefault</hask> and <hask>foldMapDefault</hask>. |
||
| − | The standard libraries provide a number of < |
+ | The standard libraries provide a number of <code>Traversable</code> instances, |
| − | including instances for < |
+ | including instances for <code>[]</code>, <code>ZipList</code>, <code>Maybe</code>, <code>((,) e)</code>, <code>Sum</code>, <code>Product</code>, <code>Either e</code>, <code>Map</code>, <code>Tree</code>, and <code>Sequence</code>. |
| − | Notably, < |
+ | Notably, <code>Set</code> is not <code>Traversable</code>, although it is <code>Foldable</code>. |
| + | |||
| + | {{Exercises| |
||
| + | # Implement <code>fmap</code> and <code>foldMap</code> using only the <code>Traversable</code> methods. (Note that the <code>Traversable</code> module provides these implementations as <code>fmapDefault</code> and <code>foldMapDefault</code>.) |
||
| + | # Implement <code>Traversable</code> instances for <code>[]</code>, <code>Maybe</code>, <code>((,) e)</code>, and <code>Either e</code>. |
||
| + | # Explain why <code>Set</code> is <code>Foldable</code> but not <code>Traversable</code>. |
||
| + | # Show that <code>Traversable</code> functors compose: that is, implement an instance for <code>Traversable (Compose f g)</code> given <code>Traversable</code> instances for <code>f</code> and <code>g</code>. |
||
| + | }} |
||
| + | |||
| + | ==Laws== |
||
| + | |||
| + | Any instance of <code>Traversable</code> must satisfy the following two laws, where <code>Identity</code> is the identity functor (as defined in the [http://hackage.haskell.org/packages/archive/transformers/latest/doc/html/Data-Functor-Identity.html <code>Data.Functor.Identity</code> module] from the <code>transformers</code> package), and <code>Compose</code> wraps the composition of two functors (as defined in [http://hackage.haskell.org/packages/archive/transformers/0.3.0.0/doc/html/Data-Functor-Compose.html <code>Data.Functor.Compose</code>]): |
||
| + | |||
| + | # <code>traverse Identity = Identity</code> |
||
| + | # <code>traverse (Compose . fmap g . f) = Compose . fmap (traverse g) . traverse f</code> |
||
| + | |||
| + | The first law essentially says that traversals cannot make up arbitrary effects. The second law explains how doing two traversals in sequence can be collapsed to a single traversal. |
||
| + | |||
| + | Additionally, suppose <code>eta</code> is an "<code>Applicative</code> morphism", that is, |
||
| + | <haskell> |
||
| + | eta :: forall a f g. (Applicative f, Applicative g) => f a -> g a |
||
| + | </haskell> |
||
| + | and <code>eta</code> preserves the <code>Applicative</code> operations: <code>eta (pure x) = pure x</code> and <code>eta (x <*> y) = eta x <*> eta y</code>. Then, by parametricity, any instance of <code>Traversable</code> satisfying the above two laws will also satisfy <code>eta . traverse f = traverse (eta . f)</code>. |
||
==Further reading== |
==Further reading== |
||
| − | The < |
+ | The <code>Traversable</code> class also had its genesis in [http://www.soi.city.ac.uk/~ross/papers/Applicative.html McBride and Paterson’s <code>Applicative</code> paper], |
| + | and is described in more detail in Gibbons and Oliveira, [http://www.comlab.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf The Essence of the Iterator Pattern], |
||
| − | <hask>Applicative</hask> paper], and is described in |
||
| + | which also contains a wealth of references to related work. |
||
| − | more detail in Gibbons and Oliveira, [http://www.comlab.ox.ac.uk/jeremy.gibbons/publications/iterator.pdf The Essence of the Iterator Pattern], which also contains a wealth of |
||
| + | |||
| − | references to related work. |
||
| + | <code>Traversable</code> forms a core component of Edward Kmett's [http://hackage.haskell.org/package/lens lens library]. Watching [https://vimeo.com/56063074 Edward's talk on the subject] is a highly recommended way to gain better insight into <code>Traversable</code>, <code>Foldable</code>, <code>Applicative</code>, and many other things besides. |
||
| + | |||
| + | For references on the <code>Traversable</code> laws, see Russell O'Connor's [http://archive.fo/7XcVE mailing list post] (and subsequent thread), and [https://arxiv.org/abs/1202.2919 this paper by Jaskelioff and Rypacek] for a more in-depth discussion. Daniel Mlot also has [http://duplode.github.io/posts/traversable-a-remix.html this very nice blog post] explaining how <code>Traversable</code> arises by considering a variant on the usual Kleisli category of a monad, which also sheds light on where the <code>Traversable</code> laws come from. |
||
| + | |||
| + | [http://elvishjerricco.github.io/2017/03/23/applicative-sorting.html This blog post by Will Fancher] shows how to use <code>Traversable</code> along with a clever choice of <code>Applicative</code> to efficiently sort any <code>Traversable</code> container. |
||
| + | |||
| + | =Bifunctor= |
||
| + | |||
| + | Recall that a <code>Functor</code> is a type of kind <code>* -> *</code> where one can "map" a function over the type parameter. <code>(Either e)</code> is a <code>Functor</code> (with <code>fmap :: (a -> b) -> Either e a -> Either e b</code>), as is <code>((,) e)</code>. But there is something oddly asymmetric about these two examples: in principle, there is no reason we can't map over the <code>e</code> instead of the <code>a</code>, for example, like so: <code>lmap :: (e -> e') -> Either e a -> Either e' a</code>. This observation leads directly to the definition of <code>Bifunctor</code>, a class for types of kind <code>* -> * -> *</code> where one can functorially map over ''both'' type parameters. |
||
| + | |||
| + | ==Definition== |
||
| + | |||
| + | Here is the type class declaration for <code>Bifunctor</code>, defined |
||
| + | in <code>Data.Bifunctor</code> (since <code>base-4.8</code>, which came with GHC 7.10): |
||
| + | |||
| + | <haskell> |
||
| + | class Bifunctor p where |
||
| + | bimap :: (a -> b) -> (c -> d) -> p a c -> p b d |
||
| + | |||
| + | first :: (a -> b) -> p a c -> p b c |
||
| + | second :: (b -> c) -> p a b -> p a c |
||
| + | </haskell> |
||
| + | |||
| + | We can infer from the fact that <code>p</code> is applied to two type |
||
| + | arguments that its kind must be <code>* -> * -> *</code>. The most |
||
| + | fundamental method of the <code>Bifunctor</code> class is |
||
| + | <code>bimap</code>, which allows mapping over both type arguments at |
||
| + | once. For example, |
||
| + | |||
| + | <haskell> |
||
| + | bimap (+1) length (4, [1,2,3]) = (5,3) |
||
| + | </haskell> |
||
| + | |||
| + | <code>first</code> and <code>second</code> are also provided for |
||
| + | mapping over only one type argument at a time. One is required to |
||
| + | define either <code>bimap</code>, or both <code>first</code> and |
||
| + | <code>second</code>, since default definitions are provided for each |
||
| + | in terms of the others, namely: |
||
| + | |||
| + | <haskell> |
||
| + | bimap f g = first f . second g |
||
| + | |||
| + | first f = bimap f id |
||
| + | second g = bimap id g |
||
| + | </haskell> |
||
| + | |||
| + | ==Laws== |
||
| + | |||
| + | The laws for <code>Bifunctor</code> are entirely analogous to the laws |
||
| + | for <code>Functor</code>. First, mapping with the identity function |
||
| + | should have no effect: |
||
| + | |||
| + | <haskell> |
||
| + | bimap id id = id |
||
| + | first id = id |
||
| + | second id = id |
||
| + | </haskell> |
||
| + | |||
| + | Second, mapping with a composition should be the same as a composition |
||
| + | of maps: |
||
| + | |||
| + | <haskell> |
||
| + | bimap (f . g) (h . i) = bimap f h . bimap g i |
||
| + | |||
| + | first (f . g) = first f . first g |
||
| + | second (f . g) = second f . second g |
||
| + | </haskell> |
||
| + | |||
| + | These composition laws actually come "for free" (that is, by |
||
| + | parametricity) once the identity laws are satisfied. One can also |
||
| + | check that the default implementations of <code>first</code> and |
||
| + | <code>second</code> will satisfy the requisite laws if and only if |
||
| + | <code>bimap</code> does, and vice versa. |
||
| + | |||
| + | There is one additional law that relates <code>bimap</code>, |
||
| + | <code>first</code>, and <code>second</code>, namely, |
||
| + | |||
| + | <haskell> |
||
| + | bimap f g = first f . second g |
||
| + | </haskell> |
||
| + | |||
| + | However, this law will hold automatically if one defines only |
||
| + | <code>bimap</code>, or only <code>first</code> and |
||
| + | <code>second</code>, using the default implementation for the others. |
||
| + | So you only need to worry about this law if for some reason (''e.g.'' |
||
| + | efficiency) you define all three of the methods by hand. |
||
| + | |||
| + | One might wonder about the symmetric law <code>bimap f g = second g |
||
| + | . first f</code>; it turns out that once <code>bimap f g = first f |
||
| + | . second g</code> is satisfied, the symmetric version [https://byorgey.wordpress.com/2018/03/30/parametricity-for-bifunctor/ also follows from parametricity]. |
||
| + | |||
| + | In summary, there are many laws that can be stated, but most of them |
||
| + | follow automatically from default definitions or from parametricity. |
||
| + | For example, if you define only <code>bimap</code>, then the only law |
||
| + | you actually need to check is <code>bimap id id = id</code>; all the |
||
| + | other laws come for free. Likewise, if you define only |
||
| + | <code>first</code> and <code>second</code>, you only need to check |
||
| + | that <code>first id = id</code> and <code>second id = id</code>. |
||
| + | |||
| + | ==Instances== |
||
| + | |||
| + | * <code>(,)</code> and <code>Either</code> are instances in the evident way. |
||
| + | |||
| + | * Some larger tuple constructors are also instances; for example, the instance for <code>(,,)</code> maps over the last two components, leaving the first alone. Why anyone would ever want to use this is unclear. |
||
| + | |||
| + | * A value of type <code>Const a b</code> (to be discussed more in a later section) consists simply of a value of type <code>a</code>; <code>bimap f g</code> maps <code>f</code> over the <code>a</code> and ignores <code>g</code>. |
||
=Category= |
=Category= |
||
| − | < |
+ | <code>Category</code> is a relatively recent addition to the Haskell standard libraries. It generalizes the notion of function composition to general “morphisms”. |
| − | libraries; you may or may not have it installed depending on the |
||
| − | version of your <hask>base</hask> package. It generalizes the notion of |
||
| − | function composition to general “morphisms”. |
||
| + | {{note|GHC 7.6.1 changed its rules regarding types and type variables. Now, any operator at the type level is treated as a type ''constructor'' rather than a type ''variable''; prior to GHC 7.6.1 it was possible to use <code>(~>)</code> instead of <code>`arr`</code>. For more information, see [http://archive.fo/weS2f the discussion on the GHC-users mailing list]. For a new approach to nice arrow notation that works with GHC 7.6.1, see [http://archive.fo/HhdvB this message] and also [http://archive.fo/iGx6W this message] from Edward Kmett, though for simplicity I haven't adopted it here.}} |
||
| − | The definition of the <hask>Category</hask> type class (from |
||
| + | The definition of the <code>Category</code> type class (from |
||
| − | <hask>Control.Category</hask>—[http://haskell.org/ghc/docs/latest/html/libraries/base/Control-Category.html haddock]) is shown below. For ease of reading, note that I have used an |
||
| + | <code>Control.Category</code>; [{{HackageDocs|base|Control-Category}} haddock]) is shown below. For ease of reading, note that I have used an infix type variable <code>`arr`</code>, in parallel with the infix function type constructor <code>(->)</code>. {{noteref}} This syntax is not part of Haskell 2010. The second definition shown is the one used in the standard libraries. For the remainder of this document, I will use the infix type constructor <code>`arr`</code> for <code>Category</code> as well as <code>Arrow</code>. |
||
| − | infix type constructor <hask>(~>)</hask>, much like the infix function type |
||
| − | constructor <hask>(->)</hask>. This syntax is not part of Haskell 98. |
||
| − | The second definition shown is the one used in the standard libraries. |
||
| − | For the remainder of this document, I will use the infix type |
||
| − | constructor <hask>(~>)</hask> for <hask>Category</hask> as well as <hask>Arrow</hask>. |
||
<haskell> |
<haskell> |
||
| − | class Category |
+ | class Category arr where |
| − | id :: a |
+ | id :: a `arr` a |
| − | (.) :: (b |
+ | (.) :: (b `arr` c) -> (a `arr` b) -> (a `arr` c) |
-- The same thing, with a normal (prefix) type constructor |
-- The same thing, with a normal (prefix) type constructor |
||
| Line 1,028: | Line 1,651: | ||
</haskell> |
</haskell> |
||
| + | Note that an instance of <code>Category</code> should be a type which takes two type arguments, that is, something of kind <code>* -> * -> *</code>. It is instructive to imagine the type variable <code>cat</code> replaced by the function constructor <code>(->)</code>: indeed, in this case we recover precisely the familiar identity function <code>id</code> and function composition operator <code>(.)</code> defined in the standard <code>Prelude</code>. |
||
| − | Note that an instance of <hask>Category</hask> should be a type constructor which |
||
| − | takes two type arguments, that is, something of kind <hask>* -> * -> *</hask>. It |
||
| − | is instructive to imagine the type constructor variable <hask>cat</hask> replaced |
||
| − | by the function constructor <hask>(->)</hask>: indeed, in this case we recover |
||
| − | precisely the familiar identity function <hask>id</hask> and function composition |
||
| − | operator <hask>(.)</hask> defined in the standard <hask>Prelude</hask>. |
||
| − | Of course, the < |
+ | Of course, the <code>Category</code> module provides exactly such an instance of |
| − | < |
+ | <code>Category</code> for <code>(->)</code>. But it also provides one other instance, shown below, which should be familiar from the previous discussion of the <code>Monad</code> laws. <code>Kleisli m a b</code>, as defined in the <code>Control.Arrow</code> module, is just a <code>newtype</code> wrapper around <code>a -> m b</code>. |
| − | below, which should be familiar from the |
||
| − | previous discussion of the <hask>Monad</hask> laws. <hask>Kleisli m a b</hask>, as defined |
||
| − | in the <hask>Control.Arrow</hask> module, is just a <hask>newtype</hask> wrapper around <hask>a -> m b</hask>. |
||
<haskell> |
<haskell> |
||
| Line 1,045: | Line 1,660: | ||
instance Monad m => Category (Kleisli m) where |
instance Monad m => Category (Kleisli m) where |
||
| + | id :: Kleisli m a a |
||
id = Kleisli return |
id = Kleisli return |
||
| + | |||
| + | (.) :: Kleisli m b c -> Kleisli m a b -> Kleisli m a c |
||
Kleisli g . Kleisli h = Kleisli (h >=> g) |
Kleisli g . Kleisli h = Kleisli (h >=> g) |
||
</haskell> |
</haskell> |
||
| − | The only |
+ | The only laws that <code>Category</code> instances should satisfy are that <code>id</code> should be the identity of <code>(.)</code>, and <code>(.)</code> should be associative. This is kind of like being a monoid, except that, unlike with monoids, not any two values can be composed with <code>(.)</code>---their types have to match up. |
| − | <hask>(.)</hask> should form a monoid—that is, <hask>id</hask> should be the identity of |
||
| − | <hask>(.)</hask>, and <hask>(.)</hask> should be associative. |
||
| − | Finally, the < |
+ | Finally, the <code>Category</code> module exports two additional operators: |
| − | < |
+ | <code>(<<<)</code>, which is just a synonym for <code>(.)</code>, and <code>(>>>)</code>, which is <code>(.)</code> with its arguments reversed. (In previous versions of the libraries, these operators were defined as part of the <code>Arrow</code> class.) |
| − | <hask>(.)</hask> with its arguments reversed. (In previous versions of the |
||
| − | libraries, these operators were defined as part of the <hask>Arrow</hask> class.) |
||
==Further reading== |
==Further reading== |
||
| + | The name <code>Category</code> is a bit misleading, since the <code>Category</code> class cannot represent arbitrary categories, but only categories whose objects are objects of <code>Hask</code>, the category of Haskell types. For a more general treatment of categories within Haskell, see the [http://hackage.haskell.org/package/category-extras category-extras package]. For more about category theory in general, see the excellent [http://en.wikibooks.org/wiki/Haskell/Category_theory Haskell wikibook page], |
||
| − | The name <hask>Category</hask> is a bit misleading, since the <hask>Category</hask> class |
||
| + | [http://books.google.com/books/about/Category_theory.html?id=-MCJ6x2lC7oC Steve Awodey’s new book], Benjamin Pierce’s [http://books.google.com/books/about/Basic_category_theory_for_computer_scien.html?id=ezdeaHfpYPwC Basic category theory for computer scientists], or [http://folli.loria.fr/cds/1999/esslli99/courses/barr-wells.html Barr and Wells category theory lecture notes]. [http://dekudekuplex.wordpress.com/2009/01/19/motivating-learning-category-theory-for-non-mathematicians/ Benjamin Russell’s blog post] |
||
| − | cannot represent arbitrary categories, but only categories whose |
||
| + | is another good source of motivation and category theory links. You certainly don’t need to know any category theory to be a successful and productive Haskell programmer, but it does lend itself to much deeper appreciation of Haskell’s underlying theory. |
||
| − | objects are objects of <hask>Hask</hask>, the category of Haskell types. For a |
||
| − | more general treatment of categories within Haskell, see the |
||
| − | [http://hackage.haskell.org/package/category-extras category-extras package]. For more about |
||
| − | category theory in general, see the excellent [http://en.wikibooks.org/wiki/Haskell/Category_theory Haskell wikibook page], |
||
| − | [http://books.google.com/books/about/Category_theory.html?id=-MCJ6x2lC7oC Steve Awodey’s new book], |
||
| − | Benjamin Pierce’s |
||
| − | [http://books.google.com/books/about/Basic_category_theory_for_computer_scien.html?id=ezdeaHfpYPwC Basic category theory for computer scientists], or |
||
| − | [http://folli.loria.fr/cds/1999/esslli99/courses/barr-wells.html Barr and Wells’s category theory lecture notes]. [http://dekudekuplex.wordpress.com/2009/01/19/motivating-learning-category-theory-for-non-mathematicians/ Benjamin Russell’s blog post] |
||
| − | is another good source of motivation and |
||
| − | category theory links. You certainly don’t need to know any category |
||
| − | theory to be a successful and productive Haskell programmer, but it |
||
| − | does lend itself to much deeper appreciation of Haskell’s underlying |
||
| − | theory. |
||
=Arrow= |
=Arrow= |
||
| − | The < |
+ | The <code>Arrow</code> class represents another abstraction of computation, in a |
| − | similar vein to < |
+ | similar vein to <code>Monad</code> and <code>Applicative</code>. However, unlike <code>Monad</code> |
| − | and < |
+ | and <code>Applicative</code>, whose types only reflect their output, the type of |
| − | an < |
+ | an <code>Arrow</code> computation reflects both its input and output. Arrows |
| − | generalize functions: if < |
+ | generalize functions: if <code>arr</code> is an instance of <code>Arrow</code>, a value of |
| − | type < |
+ | type <code>b `arr` c</code> can be thought of as a computation which takes values of |
| − | type < |
+ | type <code>b</code> as input, and produces values of type <code>c</code> as output. In the |
| − | < |
+ | <code>(->)</code> instance of <code>Arrow</code> this is just a pure function; in general, however, |
an arrow may represent some sort of “effectful” computation. |
an arrow may represent some sort of “effectful” computation. |
||
==Definition== |
==Definition== |
||
| − | The definition of the < |
+ | The definition of the <code>Arrow</code> type class, from |
| − | < |
+ | <code>Control.Arrow</code> ([{{HackageDocs|base|Control-Arrow}} haddock]), is: |
<haskell> |
<haskell> |
||
| − | class Category |
+ | class Category arr => Arrow arr where |
| − | arr :: (b -> c) -> (b |
+ | arr :: (b -> c) -> (b `arr` c) |
| − | first :: (b |
+ | first :: (b `arr` c) -> ((b, d) `arr` (c, d)) |
| − | second :: (b |
+ | second :: (b `arr` c) -> ((d, b) `arr` (d, c)) |
| − | (***) :: (b |
+ | (***) :: (b `arr` c) -> (b' `arr` c') -> ((b, b') `arr` (c, c')) |
| − | (&&&) :: (b |
+ | (&&&) :: (b `arr` c) -> (b `arr` c') -> (b `arr` (c, c')) |
</haskell> |
</haskell> |
||
| − | {{note|In versions of the < |
+ | {{note|In versions of the <code>base</code> |
| − | package prior to version 4, there is no < |
+ | package prior to version 4, there is no <code>Category</code> class, and the |
| − | < |
+ | <code>Arrow</code> class includes the arrow composition operator <code>(>>>)</code>. It |
| − | also includes < |
+ | also includes <code>pure</code> as a synonym for <code>arr</code>, but this was removed |
| − | since it conflicts with the < |
+ | since it conflicts with the <code>pure</code> from <code>Applicative</code>.}} |
| − | The first thing to note is the < |
+ | The first thing to note is the <code>Category</code> class constraint, which |
means that we get identity arrows and arrow composition for free: |
means that we get identity arrows and arrow composition for free: |
||
| − | given two arrows < |
+ | given two arrows <code>g :: b `arr` c</code> and <code>h :: c `arr` d</code>, we can form their |
| − | composition < |
+ | composition <code>g >>> h :: b `arr` d</code> {{noteref}}. |
As should be a familiar pattern by now, the only methods which must be |
As should be a familiar pattern by now, the only methods which must be |
||
| − | defined when writing a new instance of < |
+ | defined when writing a new instance of <code>Arrow</code> are <code>arr</code> and <code>first</code>; |
the other methods have default definitions in terms of these, but are |
the other methods have default definitions in terms of these, but are |
||
| − | included in the < |
+ | included in the <code>Arrow</code> class so that they can be overridden with more |
efficient implementations if desired. |
efficient implementations if desired. |
||
| + | |||
| + | Note that <code>first</code> and <code>second</code> conflict with methods of the same name from <code>Data.Bifunctor</code>. If you want to use both for some reason, you will need to import one or both qualified. It used to be common to import <code>Control.Arrow</code> just to get the <code>(->)</code> instance for use in editing pairs using <code>first</code> or <code>second</code>; now it is recommended to import <code>Data.Bifunctor</code> for this purpose instead. (Notice that for the <code>(->)</code> instance of <code>Arrow</code> and the <code>(,)</code> instance of <code>Bifunctor</code>, <code>first</code> and <code>second</code> specialize to the same type.) |
||
==Intuition== |
==Intuition== |
||
| Line 1,124: | Line 1,728: | ||
build intuition. |
build intuition. |
||
| − | * The < |
+ | * The <code>arr</code> function takes any function <code>b -> c</code> and turns it into a generalized arrow <code>b `arr` c</code>. The <code>arr</code> method justifies the claim that arrows generalize functions, since it says that we can treat any function as an arrow. It is intended that the arrow <code>arr g</code> is “pure” in the sense that it only computes <code>g</code> and has no “effects” (whatever that might mean for any particular arrow type). |
| − | * The < |
+ | * The <code>first</code> method turns any arrow from <code>b</code> to <code>c</code> into an arrow from <code>(b,d)</code> to <code>(c,d)</code>. The idea is that <code>first g</code> uses <code>g</code> to process the first element of a tuple, and lets the second element pass through unchanged. For the function instance of <code>Arrow</code>, of course, <code>first g (x,y) = (g x, y)</code>. |
| − | * The < |
+ | * The <code>second</code> function is similar to <code>first</code>, but with the elements of the tuples swapped. Indeed, it can be defined in terms of <code>first</code> using an auxiliary function <code>swap</code>, defined by <code>swap (x,y) = (y,x)</code>. |
| − | * The < |
+ | * The <code>(***)</code> operator is “parallel composition” of arrows: it takes two arrows and makes them into one arrow on tuples, which has the behavior of the first arrow on the first element of a tuple, and the behavior of the second arrow on the second element. The mnemonic is that <code>g *** h</code> is the ''product'' (hence <code>*</code>) of <code>g</code> and <code>h</code>. For the function instance of <code>Arrow</code>, we define <code>(g *** h) (x,y) = (g x, h y)</code>. The default implementation of <code>(***)</code> is in terms of <code>first</code>, <code>second</code>, and sequential arrow composition <code>(>>>)</code>. The reader may also wish to think about how to implement <code>first</code> and <code>second</code> in terms of <code>(***)</code>. |
| − | * The < |
+ | * The <code>(&&&)</code> operator is “fanout composition” of arrows: it takes two arrows <code>g</code> and <code>h</code> and makes them into a new arrow <code>g &&& h</code> which supplies its input as the input to both <code>g</code> and <code>h</code>, returning their results as a tuple. The mnemonic is that <code>g &&& h</code> performs both <code>g</code> ''and'' <code>h</code> (hence <code>&</code>) on its input. For functions, we define <code>(g &&& h) x = (g x, h x)</code>. |
==Instances== |
==Instances== |
||
| − | The < |
+ | The <code>Arrow</code> library itself only provides two <code>Arrow</code> instances, both |
| − | of which we have already seen: < |
+ | of which we have already seen: <code>(->)</code>, the normal function |
| − | constructor, and < |
+ | constructor, and <code>Kleisli m</code>, which makes functions of |
| − | type < |
+ | type <code>a -> m b</code> into <code>Arrow</code>s for any <code>Monad m</code>. These instances are: |
<haskell> |
<haskell> |
||
instance Arrow (->) where |
instance Arrow (->) where |
||
| + | arr :: (b -> c) -> (b -> c) |
||
arr g = g |
arr g = g |
||
| + | |||
| + | first :: (b -> c) -> ((b,d) -> (c,d)) |
||
first g (x,y) = (g x, y) |
first g (x,y) = (g x, y) |
||
| Line 1,149: | Line 1,756: | ||
instance Monad m => Arrow (Kleisli m) where |
instance Monad m => Arrow (Kleisli m) where |
||
| + | arr :: (b -> c) -> Kleisli m b c |
||
arr f = Kleisli (return . f) |
arr f = Kleisli (return . f) |
||
| + | |||
| + | first :: Kleisli m b c -> Kleisli m (b,d) (c,d) |
||
first (Kleisli f) = Kleisli (\ ~(b,d) -> do c <- f b |
first (Kleisli f) = Kleisli (\ ~(b,d) -> do c <- f b |
||
return (c,d) ) |
return (c,d) ) |
||
| Line 1,158: | Line 1,768: | ||
{{note|See [http://dx.doi.org/10.1016/S0167-6423(99)00023-4 John Hughes: Generalising monads to arrows]; [http://homepages.inf.ed.ac.uk/wadler/papers/arrows/arrows.pdf Sam Lindley, Philip Wadler, Jeremy Yallop: The arrow calculus]; [http://www.soi.city.ac.uk/~ross/papers/fop.html Ross Paterson: Programming with Arrows].}} |
{{note|See [http://dx.doi.org/10.1016/S0167-6423(99)00023-4 John Hughes: Generalising monads to arrows]; [http://homepages.inf.ed.ac.uk/wadler/papers/arrows/arrows.pdf Sam Lindley, Philip Wadler, Jeremy Yallop: The arrow calculus]; [http://www.soi.city.ac.uk/~ross/papers/fop.html Ross Paterson: Programming with Arrows].}} |
||
| − | There are quite a few laws that instances of < |
+ | There are quite a few laws that instances of <code>Arrow</code> should |
satisfy {{noteref}}: |
satisfy {{noteref}}: |
||
| Line 1,175: | Line 1,785: | ||
Note that this version of the laws is slightly different than the laws given in the |
Note that this version of the laws is slightly different than the laws given in the |
||
first two above references, since several of the laws have now been |
first two above references, since several of the laws have now been |
||
| − | subsumed by the < |
+ | subsumed by the <code>Category</code> laws (in particular, the requirements that |
| − | < |
+ | <code>id</code> is the identity arrow and that <code>(>>>)</code> is associative). The laws |
shown here follow those in Paterson’s Programming with Arrows, which uses the |
shown here follow those in Paterson’s Programming with Arrows, which uses the |
||
| − | < |
+ | <code>Category</code> class. |
{{note|Unless category-theory-induced insomnolence is your cup of tea.}} |
{{note|Unless category-theory-induced insomnolence is your cup of tea.}} |
||
| − | The reader is advised not to lose too much sleep over the < |
+ | The reader is advised not to lose too much sleep over the <code>Arrow</code> |
laws {{noteref}}, since it is not essential to understand them in order to |
laws {{noteref}}, since it is not essential to understand them in order to |
||
| − | program with arrows. There are also laws that < |
+ | program with arrows. There are also laws that <code>ArrowChoice</code>, |
| − | < |
+ | <code>ArrowApply</code>, and <code>ArrowLoop</code> instances should satisfy; the interested |
reader should consult [http://www.soi.city.ac.uk/~ross/papers/fop.html Paterson: Programming with Arrows]. |
reader should consult [http://www.soi.city.ac.uk/~ross/papers/fop.html Paterson: Programming with Arrows]. |
||
==ArrowChoice== |
==ArrowChoice== |
||
| − | Computations built using the < |
+ | Computations built using the <code>Arrow</code> class, like those built using |
| − | the < |
+ | the <code>Applicative</code> class, are rather inflexible: the structure of the computation |
is fixed at the outset, and there is no ability to choose between |
is fixed at the outset, and there is no ability to choose between |
||
alternate execution paths based on intermediate results. |
alternate execution paths based on intermediate results. |
||
| − | The < |
+ | The <code>ArrowChoice</code> class provides exactly such an ability: |
<haskell> |
<haskell> |
||
| − | class Arrow |
+ | class Arrow arr => ArrowChoice arr where |
| − | left :: (b |
+ | left :: (b `arr` c) -> (Either b d `arr` Either c d) |
| − | right :: (b |
+ | right :: (b `arr` c) -> (Either d b `arr` Either d c) |
| − | (+++) :: (b |
+ | (+++) :: (b `arr` c) -> (b' `arr` c') -> (Either b b' `arr` Either c c') |
| − | (|||) :: (b |
+ | (|||) :: (b `arr` d) -> (c `arr` d) -> (Either b c `arr` d) |
</haskell> |
</haskell> |
||
| − | A comparison of < |
+ | A comparison of <code>ArrowChoice</code> to <code>Arrow</code> will reveal a striking |
| − | parallel between < |
+ | parallel between <code>left</code>, <code>right</code>, <code>(+++)</code>, <code>(|||)</code> and <code>first</code>, |
| − | < |
+ | <code>second</code>, <code>(***)</code>, <code>(&&&)</code>, respectively. Indeed, they are dual: |
| − | < |
+ | <code>first</code>, <code>second</code>, <code>(***)</code>, and <code>(&&&)</code> all operate on product types |
| − | (tuples), and < |
+ | (tuples), and <code>left</code>, <code>right</code>, <code>(+++)</code>, and <code>(|||)</code> are the |
corresponding operations on sum types. In general, these operations |
corresponding operations on sum types. In general, these operations |
||
| − | create arrows whose inputs are tagged with < |
+ | create arrows whose inputs are tagged with <code>Left</code> or <code>Right</code>, and can |
choose how to act based on these tags. |
choose how to act based on these tags. |
||
| − | * If < |
+ | * If <code>g</code> is an arrow from <code>b</code> to <code>c</code>, then <code>left g</code> is an arrow from <code>Either b d</code> to <code>Either c d</code>. On inputs tagged with <code>Left</code>, the <code>left g</code> arrow has the behavior of <code>g</code>; on inputs tagged with <code>Right</code>, it behaves as the identity. |
| − | * The < |
+ | * The <code>right</code> function, of course, is the mirror image of <code>left</code>. The arrow <code>right g</code> has the behavior of <code>g</code> on inputs tagged with <code>Right</code>. |
| − | * The < |
+ | * The <code>(+++)</code> operator performs “multiplexing”: <code>g +++ h</code> behaves as <code>g</code> on inputs tagged with <code>Left</code>, and as <code>h</code> on inputs tagged with <code>Right</code>. The tags are preserved. The <code>(+++)</code> operator is the ''sum'' (hence <code>+</code>) of two arrows, just as <code>(***)</code> is the product. |
| − | * The < |
+ | * The <code>(|||)</code> operator is “merge” or “fanin”: the arrow <code>g ||| h</code> behaves as <code>g</code> on inputs tagged with <code>Left</code>, and <code>h</code> on inputs tagged with <code>Right</code>, but the tags are discarded (hence, <code>g</code> and <code>h</code> must have the same output type). The mnemonic is that <code>g ||| h</code> performs either <code>g</code> ''or'' <code>h</code> on its input. |
| − | The < |
+ | The <code>ArrowChoice</code> class allows computations to choose among a finite number of execution paths, based on intermediate results. The possible |
| − | execution paths must be known in advance, and explicitly assembled with < |
+ | execution paths must be known in advance, and explicitly assembled with <code>(+++)</code> or <code>(|||)</code>. However, sometimes more flexibility is |
| − | needed: we would like to be able to ''compute'' an arrow from intermediate results, and use this computed arrow to continue the computation. This is the power given to us by < |
+ | needed: we would like to be able to ''compute'' an arrow from intermediate results, and use this computed arrow to continue the computation. This is the power given to us by <code>ArrowApply</code>. |
==ArrowApply== |
==ArrowApply== |
||
| − | The < |
+ | The <code>ArrowApply</code> type class is: |
<haskell> |
<haskell> |
||
| − | class Arrow |
+ | class Arrow arr => ArrowApply arr where |
| − | app :: (b |
+ | app :: (b `arr` c, b) `arr` c |
</haskell> |
</haskell> |
||
If we have computed an arrow as the output of some previous |
If we have computed an arrow as the output of some previous |
||
| − | computation, then < |
+ | computation, then <code>app</code> allows us to apply that arrow to an input, |
| − | producing its output as the output of < |
+ | producing its output as the output of <code>app</code>. As an exercise, the |
| − | reader may wish to use < |
+ | reader may wish to use <code>app</code> to implement an alternative “curried” |
| − | version, < |
+ | version, <code>app2 :: b `arr` ((b `arr` c) `arr` c)</code>. |
This notion of being able to ''compute'' a new computation |
This notion of being able to ''compute'' a new computation |
||
may sound familiar: |
may sound familiar: |
||
| − | this is exactly what the monadic bind operator < |
+ | this is exactly what the monadic bind operator <code>(>>=)</code> does. It |
| − | should not particularly come as a surprise that < |
+ | should not particularly come as a surprise that <code>ArrowApply</code> and |
| − | < |
+ | <code>Monad</code> are exactly equivalent in expressive power. In particular, |
| − | < |
+ | <code>Kleisli m</code> can be made an instance of <code>ArrowApply</code>, and any instance |
| − | of < |
+ | of <code>ArrowApply</code> can be made a <code>Monad</code> (via the <code>newtype</code> wrapper |
| − | < |
+ | <code>ArrowMonad</code>). As an exercise, the reader may wish to try |
implementing these instances: |
implementing these instances: |
||
<haskell> |
<haskell> |
||
| + | class Arrow arr => ArrowApply arr where |
||
| + | app :: (b `arr` c, b) `arr` c |
||
| + | |||
instance Monad m => ArrowApply (Kleisli m) where |
instance Monad m => ArrowApply (Kleisli m) where |
||
| + | app :: Kleisli m (Kleisli m b c, b) c |
||
app = -- exercise |
app = -- exercise |
||
| Line 1,257: | Line 1,871: | ||
instance ArrowApply a => Monad (ArrowMonad a) where |
instance ArrowApply a => Monad (ArrowMonad a) where |
||
| + | return :: b -> ArrowMonad a b |
||
return = -- exercise |
return = -- exercise |
||
| + | |||
| + | (>>=) :: ArrowMonad a a -> (a -> ArrowMonad a b) -> ArrowMonad a b |
||
(ArrowMonad a) >>= k = -- exercise |
(ArrowMonad a) >>= k = -- exercise |
||
</haskell> |
</haskell> |
||
| Line 1,263: | Line 1,880: | ||
==ArrowLoop== |
==ArrowLoop== |
||
| − | The < |
+ | The <code>ArrowLoop</code> type class is: |
<haskell> |
<haskell> |
||
| Line 1,274: | Line 1,891: | ||
It describes arrows that can use recursion to compute results, and is |
It describes arrows that can use recursion to compute results, and is |
||
| − | used to desugar the < |
+ | used to desugar the <code>rec</code> construct in arrow notation (described |
below). |
below). |
||
| − | Taken by itself, the type of the < |
+ | Taken by itself, the type of the <code>loop</code> method does not seem to tell |
| − | us much. Its intention, however, is a generalization of the < |
+ | us much. Its intention, however, is a generalization of the <code>trace</code> |
| − | function which is also shown. The < |
+ | function which is also shown. The <code>d</code> component of the first arrow’s |
output is fed back in as its own input. In other words, the arrow |
output is fed back in as its own input. In other words, the arrow |
||
| − | < |
+ | <code>loop g</code> is obtained by recursively “fixing” the second component of |
| − | the input to < |
+ | the input to <code>g</code>. |
| − | It can be a bit difficult to grok what the < |
+ | It can be a bit difficult to grok what the <code>trace</code> function is doing. |
| − | How can < |
+ | How can <code>d</code> appear on the left and right sides of the <code>let</code>? Well, |
this is Haskell’s laziness at work. There is not space here for a |
this is Haskell’s laziness at work. There is not space here for a |
||
full explanation; the interested reader is encouraged to study the |
full explanation; the interested reader is encouraged to study the |
||
| − | standard < |
+ | standard <code>fix</code> function, and to read [http://www.soi.city.ac.uk/~ross/papers/fop.html Paterson’s arrow tutorial]. |
==Arrow notation== |
==Arrow notation== |
||
| Line 1,300: | Line 1,917: | ||
reassociate, and generally mangle tuples as necessary. This problem |
reassociate, and generally mangle tuples as necessary. This problem |
||
is solved by the special arrow notation supported by GHC, similar to |
is solved by the special arrow notation supported by GHC, similar to |
||
| − | < |
+ | <code>do</code> notation for monads, that allows names to be assigned to |
intermediate results while building up arrow computations. An example |
intermediate results while building up arrow computations. An example |
||
arrow implemented using arrow notation, taken from |
arrow implemented using arrow notation, taken from |
||
| Line 1,306: | Line 1,923: | ||
<haskell> |
<haskell> |
||
| − | class ArrowLoop |
+ | class ArrowLoop arr => ArrowCircuit arr where |
| − | delay :: b -> (b |
+ | delay :: b -> (b `arr` b) |
| − | counter :: ArrowCircuit |
+ | counter :: ArrowCircuit arr => Bool `arr` Int |
counter = proc reset -> do |
counter = proc reset -> do |
||
rec output <- idA -< if reset then 0 else next |
rec output <- idA -< if reset then 0 else next |
||
| Line 1,320: | Line 1,937: | ||
There is not space here for a full explanation of arrow notation; the |
There is not space here for a full explanation of arrow notation; the |
||
| − | interested reader should consult |
+ | interested reader should consult |
| − | notation], or his later [http://www.soi.city.ac.uk/~ross/papers/fop.html |
+ | [http://www.soi.city.ac.uk/~ross/papers/notation.html Paterson’s paper introducing the notation], or his later [http://www.soi.city.ac.uk/~ross/papers/fop.html tutorial which presents a simplified version]. |
| − | tutorial which presents a simplified version]. |
||
==Further reading== |
==Further reading== |
||
| Line 1,328: | Line 1,944: | ||
An excellent starting place for the student of arrows is the [http://www.haskell.org/arrows/ arrows web page], which contains an |
An excellent starting place for the student of arrows is the [http://www.haskell.org/arrows/ arrows web page], which contains an |
||
introduction and many references. Some key papers on arrows include |
introduction and many references. Some key papers on arrows include |
||
| − | + | Hughes’ original paper introducing arrows, [http://dx.doi.org/10.1016/S0167-6423(99)00023-4 Generalising monads to arrows], and [http://www.soi.city.ac.uk/~ross/papers/notation.html Paterson’s paper on arrow notation]. |
|
Both Hughes and Paterson later wrote accessible tutorials intended for a broader |
Both Hughes and Paterson later wrote accessible tutorials intended for a broader |
||
audience: [http://www.soi.city.ac.uk/~ross/papers/fop.html Paterson: Programming with Arrows] and [http://www.cse.chalmers.se/~rjmh/afp-arrows.pdf Hughes: Programming with Arrows]. |
audience: [http://www.soi.city.ac.uk/~ross/papers/fop.html Paterson: Programming with Arrows] and [http://www.cse.chalmers.se/~rjmh/afp-arrows.pdf Hughes: Programming with Arrows]. |
||
| − | Although |
+ | Although Hughes’ goal in defining the <code>Arrow</code> class was to |
| − | generalize < |
+ | generalize <code>Monad</code>s, and it has been said that <code>Arrow</code> lies “between |
| − | < |
+ | <code>Applicative</code> and <code>Monad</code>” in power, they are not directly |
comparable. The precise relationship remained in some confusion until |
comparable. The precise relationship remained in some confusion until |
||
[http://homepages.inf.ed.ac.uk/wadler/papers/arrows-and-idioms/arrows-and-idioms.pdf analyzed by Lindley, Wadler, and Yallop], who |
[http://homepages.inf.ed.ac.uk/wadler/papers/arrows-and-idioms/arrows-and-idioms.pdf analyzed by Lindley, Wadler, and Yallop], who |
||
also invented a new calculus of arrows, based on the lambda calculus, |
also invented a new calculus of arrows, based on the lambda calculus, |
||
which considerably simplifies the presentation of the arrow laws |
which considerably simplifies the presentation of the arrow laws |
||
| − | (see [http://homepages.inf.ed.ac.uk/wadler/papers/arrows/arrows.pdf The arrow calculus]). |
+ | (see [http://homepages.inf.ed.ac.uk/wadler/papers/arrows/arrows.pdf The arrow calculus]). There is also a precise technical sense in which [http://just-bottom.blogspot.de/2010/04/programming-with-effects-story-so-far.html <code>Arrow</code> can be seen as the intersection of <code>Applicative</code> and <code>Category</code>]. |
| − | Some examples of < |
+ | Some examples of <code>Arrow</code>s include [https://wiki.haskell.org/Yampa Yampa], the |
[http://www.fh-wedel.de/~si/HXmlToolbox/ Haskell XML Toolkit], and the functional GUI library [[Grapefruit]]. |
[http://www.fh-wedel.de/~si/HXmlToolbox/ Haskell XML Toolkit], and the functional GUI library [[Grapefruit]]. |
||
Some extensions to arrows have been explored; for example, the |
Some extensions to arrows have been explored; for example, the |
||
| − | [http:// |
+ | <code>BiArrow</code>s of Alimarine et al. ([http://wiki.clean.cs.ru.nl/download/papers/2005/alia2005-biarrowsHaskellWorkshop.pdf "There and Back Again: Arrows for Invertible Programming"]), for two-way instead of one-way |
computation. |
computation. |
||
| − | The Haskell wiki has [[Research papers/Monads and Arrows|links to many additional research papers relating to < |
+ | The Haskell wiki has [[Research papers/Monads and Arrows|links to many additional research papers relating to <code>Arrow</code>s]]. |
=Comonad= |
=Comonad= |
||
| − | The final type class we will examine is < |
+ | The final type class we will examine is <code>Comonad</code>. The <code>Comonad</code> class |
| − | is the categorical dual of < |
+ | is the categorical dual of <code>Monad</code>; that is, <code>Comonad</code> is like <code>Monad</code> |
but with all the function arrows flipped. It is not actually in the |
but with all the function arrows flipped. It is not actually in the |
||
standard Haskell libraries, but it has seen some interesting uses |
standard Haskell libraries, but it has seen some interesting uses |
||
| Line 1,361: | Line 1,977: | ||
==Definition== |
==Definition== |
||
| − | The < |
+ | The <code>Comonad</code> type class, defined in the <code>Control.Comonad</code> module of |
| − | the [http://hackage.haskell.org/package/ |
+ | the [http://hackage.haskell.org/package/comonad comonad library], is: |
<haskell> |
<haskell> |
||
| − | class Functor |
+ | class Functor w => Comonad w where |
| − | extract :: |
+ | extract :: w a -> a |
| − | class Copointed w => Comonad w where |
||
duplicate :: w a -> w (w a) |
duplicate :: w a -> w (w a) |
||
| + | duplicate = extend id |
||
| + | |||
extend :: (w a -> b) -> w a -> w b |
extend :: (w a -> b) -> w a -> w b |
||
| + | extend f = fmap f . duplicate |
||
</haskell> |
</haskell> |
||
| − | As you can see, < |
+ | As you can see, <code>extract</code> is the dual of <code>return</code>, <code>duplicate</code> is the dual of <code>join</code>, and <code>extend</code> is the dual of <code>(=<<)</code>. The definition of <code>Comonad</code> is a bit redundant, giving the programmer the choice on whether extend or duplicate are implemented; the other operation then has a default implementation. |
| − | dual of <hask>join</hask>, and <hask>extend</hask> is the dual of <hask>(>>=)</hask> (although its |
||
| − | arguments are in a different order). The definition |
||
| − | of <hask>Comonad</hask> is a bit redundant (after all, the <hask>Monad</hask> class does not |
||
| − | need <hask>join</hask>), but this is so that a <hask>Comonad</hask> can be defined by <hask>fmap</hask>, |
||
| − | <hask>extract</hask>, and ''either'' <hask>duplicate</hask> or <hask>extend</hask>. Each has a |
||
| − | default implementation in terms of the other. |
||
| − | A prototypical example of a < |
+ | A prototypical example of a <code>Comonad</code> instance is: |
<haskell> |
<haskell> |
||
-- Infinite lazy streams |
-- Infinite lazy streams |
||
data Stream a = Cons a (Stream a) |
data Stream a = Cons a (Stream a) |
||
| − | |||
| − | instance Functor Stream where |
||
| − | fmap g (Cons x xs) = Cons (g x) (fmap g xs) |
||
| − | |||
| − | instance Copointed Stream where |
||
| − | extract (Cons x _) = x |
||
-- 'duplicate' is like the list function 'tails' |
-- 'duplicate' is like the list function 'tails' |
||
| Line 1,398: | Line 2,004: | ||
-- position n onwards in the old Stream |
-- position n onwards in the old Stream |
||
instance Comonad Stream where |
instance Comonad Stream where |
||
| + | extract :: Stream a -> a |
||
| + | extract (Cons x _) = x |
||
| + | |||
| + | duplicate :: Stream a -> Stream (Stream a) |
||
duplicate s@(Cons x xs) = Cons s (duplicate xs) |
duplicate s@(Cons x xs) = Cons s (duplicate xs) |
||
| + | |||
| + | extend :: (Stream a -> b) -> Stream a -> Stream b |
||
extend g s@(Cons x xs) = Cons (g s) (extend g xs) |
extend g s@(Cons x xs) = Cons (g s) (extend g xs) |
||
-- = fmap g (duplicate s) |
-- = fmap g (duplicate s) |
||
| Line 1,405: | Line 2,017: | ||
==Further reading== |
==Further reading== |
||
| − | Dan Piponi explains in a blog post what [http://blog.sigfpe.com/2006/12/evaluating-cellular-automata-is.html cellular automata have to do |
+ | Dan Piponi explains in a blog post what [http://blog.sigfpe.com/2006/12/evaluating-cellular-automata-is.html cellular automata have to do with comonads]. In another blog post, Conal Elliott has examined [http://conal.net/blog/posts/functional-interactive-behavior/ a comonadic formulation of functional reactive programming]. Sterling Clover’s blog post [http://fmapfixreturn.wordpress.com/2008/07/09/comonads-in-everyday-life/ Comonads in everyday life] explains the relationship between comonads and zippers, and how comonads can be used to design a menu system for a web site. |
| − | with comonads]. In another blog post, |
||
| − | Conal Elliott has examined [http://conal.net/blog/posts/functional-interactive-behavior/ a comonadic formulation of functional |
||
| − | reactive programming]. Sterling |
||
| − | Clover’s blog post [http://fmapfixreturn.wordpress.com/2008/07/09/comonads-in-everyday-life/ Comonads in everyday life] explains the relationship between |
||
| − | comonads and zippers, and how comonads can be used to design a menu |
||
| − | system for a web site. |
||
| − | Uustalu and Vene have a number of papers exploring ideas related to |
+ | Uustalu and Vene have a number of papers exploring ideas related to comonads and functional programming: |
| − | comonads and functional programming: |
||
* [http://dx.doi.org/10.1016/j.entcs.2008.05.029 Comonadic Notions of Computation] |
* [http://dx.doi.org/10.1016/j.entcs.2008.05.029 Comonadic Notions of Computation] |
||
| − | * [http://www. |
+ | * [http://www.ioc.ee/~tarmo/papers/sfp01-book.pdf The dual of substitution is redecoration] (Also available as [http://www.cs.ut.ee/~varmo/papers/sfp01-book.ps.gz ps.gz].) |
* [http://dx.doi.org/10.1016/j.ic.2005.08.005 Recursive coalgebras from comonads] |
* [http://dx.doi.org/10.1016/j.ic.2005.08.005 Recursive coalgebras from comonads] |
||
* [http://www.fing.edu.uy/~pardo/papers/njc01.ps.gz Recursion schemes from comonads] |
* [http://www.fing.edu.uy/~pardo/papers/njc01.ps.gz Recursion schemes from comonads] |
||
* [http://cs.ioc.ee/~tarmo/papers/essence.pdf The Essence of Dataflow Programming]. |
* [http://cs.ioc.ee/~tarmo/papers/essence.pdf The Essence of Dataflow Programming]. |
||
| + | |||
| + | Gabriel Gonzalez's [http://www.haskellforall.com/2013/02/you-could-have-invented-comonads.html Comonads are objects] points out similarities between comonads and object-oriented programming. |
||
| + | |||
| + | The [http://hackage.haskell.org/package/comonad-transformers comonad-transformers] package contains comonad transformers. |
||
=Acknowledgements= |
=Acknowledgements= |
||
| Line 1,454: | Line 2,063: | ||
=Colophon= |
=Colophon= |
||
| − | The Typeclassopedia was written by Brent Yorgey and |
+ | The Typeclassopedia was written by Brent Yorgey and initially published in March 2009. Painstakingly converted to wiki syntax by [[User:Geheimdienst]] in November 2011, after asking Brent’s permission. |
| − | If something like this |
+ | If something like this TeX to wiki syntax conversion ever needs to be done again, here are some vim commands that helped: |
* <nowiki>%s/\\section{\([^}]*\)}/=\1=/gc</nowiki> |
* <nowiki>%s/\\section{\([^}]*\)}/=\1=/gc</nowiki> |
||
| Line 1,462: | Line 2,071: | ||
* <nowiki>%s/^ *\\item /\r* /gc</nowiki> |
* <nowiki>%s/^ *\\item /\r* /gc</nowiki> |
||
* <nowiki>%s/---/—/gc</nowiki> |
* <nowiki>%s/---/—/gc</nowiki> |
||
| − | * <nowiki>%s/\$\([^$]*\)\$/<math>\1\\ <\/math>/gc</nowiki> ''Appending “\ ” forces images to be rendered. Otherwise, Mediawiki would go back and forth between one font for short <nowiki><math></nowiki> tags, and another more |
+ | * <nowiki>%s/\$\([^$]*\)\$/<math>\1\\ <\/math>/gc</nowiki> ''Appending “\ ” forces images to be rendered. Otherwise, Mediawiki would go back and forth between one font for short <nowiki><math></nowiki> tags, and another more TeX-like font for longer tags (containing more than a few characters)"" |
| − | * <nowiki>%s/|\([^|]*\)|/< |
+ | * <nowiki>%s/|\([^|]*\)|/<code>\1<\/code>/gc</nowiki> |
* <nowiki>%s/\\dots/.../gc</nowiki> |
* <nowiki>%s/\\dots/.../gc</nowiki> |
||
* <nowiki>%s/^\\label{.*$//gc</nowiki> |
* <nowiki>%s/^\\label{.*$//gc</nowiki> |
||
| Line 1,469: | Line 2,078: | ||
* <nowiki>%s/\\term{\([^}]*\)}/''\1''/gc</nowiki> |
* <nowiki>%s/\\term{\([^}]*\)}/''\1''/gc</nowiki> |
||
| − | The biggest issue was taking the academic-paper-style citations and turning them into hyperlinks with an appropriate title and an appropriate target. In most cases there was an obvious thing to do (e.g. online PDFs of the cited papers or |
+ | The biggest issue was taking the academic-paper-style citations and turning them into hyperlinks with an appropriate title and an appropriate target. In most cases there was an obvious thing to do (e.g. online PDFs of the cited papers or CiteSeer entries). Sometimes, however, it’s less clear and you might want to check the |
[[Media:Typeclassopedia.pdf|original Typeclassopedia PDF]] |
[[Media:Typeclassopedia.pdf|original Typeclassopedia PDF]] |
||
with the |
with the |
||
[http://code.haskell.org/~byorgey/TMR/Issue13/typeclassopedia.bib original bibliography file]. |
[http://code.haskell.org/~byorgey/TMR/Issue13/typeclassopedia.bib original bibliography file]. |
||
| − | To get all the citations into the main text, I first tried processing the source with |
+ | To get all the citations into the main text, I first tried processing the source with TeX or Lyx. This didn’t work due to missing unfindable packages, syntax errors, and my general ineptitude with TeX. |
I then went for the next best solution, which seemed to be extracting all instances of “\cite{something}” from the source and ''in that order'' pulling the referenced entries from the .bib file. This way you can go through the source file and sorted-references file in parallel, copying over what you need, without searching back and forth in the .bib file. I used: |
I then went for the next best solution, which seemed to be extracting all instances of “\cite{something}” from the source and ''in that order'' pulling the referenced entries from the .bib file. This way you can go through the source file and sorted-references file in parallel, copying over what you need, without searching back and forth in the .bib file. I used: |
||
Revision as of 19:21, 15 August 2019
By Brent Yorgey, byorgey@gmail.com
Originally published 12 March 2009 in issue 13 of the Monad.Reader. Ported to the Haskell wiki in November 2011 by Geheimdienst.
This is now the official version of the Typeclassopedia and supersedes the version published in the Monad.Reader. Please help update and extend it by editing it yourself or by leaving comments, suggestions, and questions on the talk page.
Abstract
The standard Haskell libraries feature a number of type classes with algebraic or category-theoretic underpinnings. Becoming a fluent Haskell hacker requires intimate familiarity with them all, yet acquiring this familiarity often involves combing through a mountain of tutorials, blog posts, mailing list archives, and IRC logs.
The goal of this document is to serve as a starting point for the student of Haskell wishing to gain a firm grasp of its standard type classes. The essentials of each type class are introduced, with examples, commentary, and extensive references for further reading.
Introduction
Have you ever had any of the following thoughts?
- What the heck is a monoid, and how is it different from a monad?
- I finally figured out how to use Parsec with do-notation, and someone told me I should use something called
Applicativeinstead. Um, what?
- Someone in the #haskell IRC channel used
(***), and when I asked Lambdabot to tell me its type, it printed out scary gobbledygook that didn’t even fit on one line! Then someone usedfmap fmap fmapand my brain exploded.
- When I asked how to do something I thought was really complicated, people started typing things like
zip.ap fmap.(id &&& wtf)and the scary thing is that they worked! Anyway, I think those people must actually be robots because there’s no way anyone could come up with that in two seconds off the top of their head.
If you have, look no further! You, too, can write and understand concise, elegant, idiomatic Haskell code with the best of them.
There are two keys to an expert Haskell hacker’s wisdom:
- Understand the types.
- Gain a deep intuition for each type class and its relationship to other type classes, backed up by familiarity with many examples.
It’s impossible to overstate the importance of the first; the patient student of type signatures will uncover many profound secrets. Conversely, anyone ignorant of the types in their code is doomed to eternal uncertainty. “Hmm, it doesn’t compile ... maybe I’ll stick in an
fmap here ... nope, let’s see ... maybe I need another (.) somewhere? ... um ...”
The second key—gaining deep intuition, backed by examples—is also important, but much more difficult to attain. A primary goal of this document is to set you on the road to gaining such intuition. However—
- There is no royal road to Haskell. —Euclid
This document can only be a starting point, since good intuition comes from hard work, not from learning the right metaphor. Anyone who reads and understands all of it will still have an arduous journey ahead—but sometimes a good starting point makes a big difference.
It should be noted that this is not a Haskell tutorial; it is assumed that the reader is already familiar with the basics of Haskell, including the standard Prelude, the type system, data types, and type classes.
The type classes we will be discussing and their interrelationships (source code for this graph can be found here):
∗ Apply can be found in the semigroupoids package, and Comonad in the comonad package.
- Solid arrows point from the general to the specific; that is, if there is an arrow from
FootoBarit means that everyBaris (or should be, or can be made into) aFoo. - Dotted lines indicate some other sort of relationship.
MonadandArrowApplyare equivalent.ApplyandComonadare greyed out since they are not actually (yet?) in the standard Haskell libraries ∗.
One more note before we begin. The original spelling of “type class” is with two words, as evidenced by, for example, the Haskell 2010 Language Report, early papers on type classes like Type classes in Haskell and Type classes: exploring the design space, and Hudak et al.’s history of Haskell. However, as often happens with two-word phrases that see a lot of use, it has started to show up as one word (“typeclass”) or, rarely, hyphenated (“type-class”). When wearing my prescriptivist hat, I prefer “type class”, but realize (after changing into my descriptivist hat) that there's probably not much I can do about it.
Instances of List and Maybe illustrates these type classes with simple examples using List and Maybe. We now begin with the simplest type class of all: Functor.
Functor
The Functor class (haddock) is the most basic and ubiquitous type class in the Haskell libraries. A simple intuition is that a Functor represents a “container” of some sort, along with the ability to apply a function uniformly to every element in the container. For example, a list is a container of elements, and we can apply a function to every element of a list, using map. As another example, a binary tree is also a container of elements, and it’s not hard to come up with a way to recursively apply a function to every element in a tree.
Another intuition is that a Functor represents some sort of “computational context”. This intuition is generally more useful, but is more difficult to explain, precisely because it is so general. Some examples later should help to clarify the Functor-as-context point of view.
In the end, however, a Functor is simply what it is defined to be; doubtless there are many examples of Functor instances that don’t exactly fit either of the above intuitions. The wise student will focus their attention on definitions and examples, without leaning too heavily on any particular metaphor. Intuition will come, in time, on its own.
Definition
Here is the type class declaration for Functor:
class Functor f where
fmap :: (a -> b) -> f a -> f b
(<$) :: a -> f b -> f a
(<$) = fmap . const
Functor is exported by the Prelude, so no special imports are needed to use it. Note that the (<$) operator is provided for convenience, with a default implementation in terms of fmap; it is included in the class just to give Functor instances the opportunity to provide a more efficient implementation than the default. To understand Functor, then, we really need to understand fmap.
First, the f a and f b in the type signature for fmap tell us that f isn’t a concrete type like Int; it is a sort of type function which takes another type as a parameter. More precisely, the kind of f must be * -> *. For example, Maybe is such a type with kind * -> *: Maybe is not a concrete type by itself (that is, there are no values of type Maybe), but requires another type as a parameter, like Maybe Integer. So it would not make sense to say instance Functor Integer, but it could make sense to say instance Functor Maybe.
Now look at the type of fmap: it takes any function from a to b, and a value of type f a, and outputs a value of type f b. From the container point of view, the intention is that fmap applies a function to each element of a container, without altering the structure of the container. From the context point of view, the intention is that fmap applies a function to a value without altering its context. Let’s look at a few specific examples.
Finally, we can understand (<$): instead of applying a function to the values a container/context, it simply replaces them with a given value. This is the same as applying a constant function, so (<$) can be implemented in terms of fmap.
Instances
∗ Recall that [] has two meanings in Haskell: it can either stand for the empty list, or, as here, it can represent the list type constructor (pronounced “list-of”). In other words, the type [a] (list-of-a) can also be written [] a.
∗ You might ask why we need a separate map function. Why not just do away with the current list-only map function, and rename fmap to map instead? Well, that’s a good question. The usual argument is that someone just learning Haskell, when using map incorrectly, would much rather see an error about lists than about Functors.
As noted before, the list constructor [] is a functor ∗; we can use the standard list function map to apply a function to each element of a list ∗. The Maybe type constructor is also a functor, representing a container which might hold a single element. The function fmap g has no effect on Nothing (there are no elements to which g can be applied), and simply applies g to the single element inside a Just. Alternatively, under the context interpretation, the list functor represents a context of nondeterministic choice; that is, a list can be thought of as representing a single value which is nondeterministically chosen from among several possibilities (the elements of the list). Likewise, the Maybe functor represents a context with possible failure. These instances are:
instance Functor [] where
fmap :: (a -> b) -> [a] -> [b]
fmap _ [] = []
fmap g (x:xs) = g x : fmap g xs
-- or we could just say fmap = map
instance Functor Maybe where
fmap :: (a -> b) -> Maybe a -> Maybe b
fmap _ Nothing = Nothing
fmap g (Just a) = Just (g a)
As an aside, in idiomatic Haskell code you will often see the letter f used to stand for both an arbitrary Functor and an arbitrary function. In this document, f represents only Functors, and g or h always represent functions, but you should be aware of the potential confusion. In practice, what f stands for should always be clear from the context, by noting whether it is part of a type or part of the code.
There are other Functor instances in the standard library as well:
Either eis an instance ofFunctor;Either e arepresents a container which can contain either a value of typea, or a value of typee(often representing some sort of error condition). It is similar toMaybein that it represents possible failure, but it can carry some extra information about the failure as well.
((,) e)represents a container which holds an “annotation” of typeealong with the actual value it holds. It might be clearer to write it as(e,), by analogy with an operator section like(1+), but that syntax is not allowed in types (although it is allowed in expressions with theTupleSectionsextension enabled). However, you can certainly think of it as(e,).
((->) e)(which can be thought of as(e ->); see above), the type of functions which take a value of typeeas a parameter, is aFunctor. As a container,(e -> a)represents a (possibly infinite) set of values ofa, indexed by values ofe. Alternatively, and more usefully,((->) e)can be thought of as a context in which a value of typeeis available to be consulted in a read-only fashion. This is also why((->) e)is sometimes referred to as the reader monad; more on this later.
IOis aFunctor; a value of typeIO arepresents a computation producing a value of typeawhich may have I/O effects. Ifmcomputes the valuexwhile producing some I/O effects, thenfmap g mwill compute the valueg xwhile producing the same I/O effects.
- Many standard types from the containers library (such as
Tree,Map, andSequence) are instances ofFunctor. A notable exception isSet, which cannot be made aFunctorin Haskell (although it is certainly a mathematical functor) since it requires anOrdconstraint on its elements;fmapmust be applicable to any typesaandb. However,Set(and other similarly restricted data types) can be made an instance of a suitable generalization ofFunctor, either by makingaandbarguments to theFunctortype class themselves, or by adding an associated constraint.
| Exercises |
|---|
|
Laws
As far as the Haskell language itself is concerned, the only requirement to be a Functor is an implementation of fmap with the proper type. Any sensible Functor instance, however, will also satisfy the functor laws, which are part of the definition of a mathematical functor. There are two:
fmap id = id
fmap (g . h) = (fmap g) . (fmap h)
∗ Technically, these laws make f and fmap together an endofunctor on Hask, the category of Haskell types (ignoring ⊥, which is a party pooper). See Wikibook: Category theory.
Together, these laws ensure that fmap g does not change the structure of a container, only the elements. Equivalently, and more simply, they ensure that fmap g changes a value without altering its context ∗.
The first law says that mapping the identity function over every item in a container has no effect. The second says that mapping a composition of two functions over every item in a container is the same as first mapping one function, and then mapping the other.
As an example, the following code is a “valid” instance of Functor (it typechecks), but it violates the functor laws. Do you see why?
-- Evil Functor instance
instance Functor [] where
fmap :: (a -> b) -> [a] -> [b]
fmap _ [] = []
fmap g (x:xs) = g x : g x : fmap g xs
Any Haskeller worth their salt would reject this code as a gruesome abomination.
Unlike some other type classes we will encounter, a given type has at most one valid instance of Functor. This can be proven via the free theorem for the type of fmap. In fact, GHC can automatically derive Functor instances for many data types.
∗ Actually, if seq/undefined are considered, it is possible to have an implementation which satisfies the first law but not the second. The rest of the comments in this section should be considered in a context where seq and undefined are excluded.
A similar argument also shows that any Functor instance satisfying the first law (fmap id = id) will automatically satisfy the second law as well. Practically, this means that only the first law needs to be checked (usually by a very straightforward induction) to ensure that a Functor instance is valid.∗
| Exercises |
|---|
|
Intuition
There are two fundamental ways to think about fmap. The first has already been mentioned: it takes two parameters, a function and a container, and applies the function “inside” the container, producing a new container. Alternately, we can think of fmap as applying a function to a value in a context (without altering the context).
Just like all other Haskell functions of “more than one parameter”, however, fmap is actually curried: it does not really take two parameters, but takes a single parameter and returns a function. For emphasis, we can write fmap’s type with extra parentheses: fmap :: (a -> b) -> (f a -> f b). Written in this form, it is apparent that fmap transforms a “normal” function (g :: a -> b) into one which operates over containers/contexts (fmap g :: f a -> f b). This transformation is often referred to as a lift; fmap “lifts” a function from the “normal world” into the “f world”.
Utility functions
There are a few more Functor-related functions which can be imported from the Data.Functor module.
(<$>)is defined as a synonym forfmap. This enables a nice infix style that mirrors the($)operator for function application. For example,f $ 3applies the functionfto 3, whereasf <$> [1,2,3]appliesfto each member of the list.($>) :: Functor f => f a -> b -> f bis justflip (<$), and can occasionally be useful. To keep them straight, you can remember that(<$)and($>)point towards the value that will be kept.void :: Functor f => f a -> f ()is a specialization of(<$), that is,void x = () <$ x. This can be used in cases where a computation computes some value but the value should be ignored.
Further reading
A good starting point for reading about the category theory behind the concept of a functor is the excellent Haskell wikibook page on category theory.
Applicative
A somewhat newer addition to the pantheon of standard Haskell type classes, applicative functors represent an abstraction lying in between Functor and Monad in expressivity, first described by McBride and Paterson. The title of their classic paper, Applicative Programming with Effects, gives a hint at the intended intuition behind the Applicative type class. It encapsulates certain sorts of “effectful” computations in a functionally pure way, and encourages an “applicative” programming style. Exactly what these things mean will be seen later.
Definition
Recall that Functor allows us to lift a “normal” function to a function on computational contexts. But fmap doesn’t allow us to apply a function which is itself in a context to a value in a context. Applicative gives us just such a tool, (<*>) (variously pronounced as "apply", "app", or "splat"). It also provides a method, pure, for embedding values in a default, “effect free” context. Here is the type class declaration for Applicative, as defined in Control.Applicative:
class Functor f => Applicative f where
pure :: a -> f a
infixl 4 <*>, *>, <*
(<*>) :: f (a -> b) -> f a -> f b
(*>) :: f a -> f b -> f b
a1 *> a2 = (id <$ a1) <*> a2
(<*) :: f a -> f b -> f a
(<*) = liftA2 const
Note that every Applicative must also be a Functor. In fact, as we will see, fmap can be implemented using the Applicative methods, so every Applicative is a functor whether we like it or not; the Functor constraint forces us to be honest.
(*>) and (<*) are provided for convenience, in case a particular instance of Applicative can provide more efficient implementations, but they are provided with default implementations. For more on these operators, see the section on Utility functions below.
∗ Recall that ($) is just function application: f $ x = f x.
As always, it’s crucial to understand the type signatures. First, consider (<*>): the best way of thinking about it comes from noting that the type of (<*>) is similar to the type of ($) ∗, but with everything enclosed in an f. In other words, (<*>) is just function application within a computational context. The type of (<*>) is also very similar to the type of fmap; the only difference is that the first parameter is f (a -> b), a function in a context, instead of a “normal” function (a -> b).
pure takes a value of any type a, and returns a context/container of type f a. The intention is that pure creates some sort of “default” container or “effect free” context. In fact, the behavior of pure is quite constrained by the laws it should satisfy in conjunction with (<*>). Usually, for a given implementation of (<*>) there is only one possible implementation of pure.
(Note that previous versions of the Typeclassopedia explained pure in terms of a type class Pointed, which can still be found in the pointed package. However, the current consensus is that Pointed is not very useful after all. For a more detailed explanation, see Why not Pointed?)
Laws
∗ See haddock for Applicative and Applicative programming with effects
Traditionally, there are four laws that Applicative instances should satisfy ∗. In some sense, they are all concerned with making sure that pure deserves its name:
- The identity law:
pure id <*> v = v
- Homomorphism:Intuitively, applying a non-effectful function to a non-effectful argument in an effectful context is the same as just applying the function to the argument and then injecting the result into the context with
pure f <*> pure x = pure (f x)
pure. - Interchange:Intuitively, this says that when evaluating the application of an effectful function to a pure argument, the order in which we evaluate the function and its argument doesn't matter.
u <*> pure y = pure ($ y) <*> u
- Composition:This one is the trickiest law to gain intuition for. In some sense it is expressing a sort of associativity property of
u <*> (v <*> w) = pure (.) <*> u <*> v <*> w
(<*>). The reader may wish to simply convince themselves that this law is type-correct.
Considered as left-to-right rewrite rules, the homomorphism, interchange, and composition laws actually constitute an algorithm for transforming any expression using pure and (<*>) into a canonical form with only a single use of pure at the very beginning and only left-nested occurrences of (<*>). Composition allows reassociating (<*>); interchange allows moving occurrences of pure leftwards; and homomorphism allows collapsing multiple adjacent occurrences of pure into one.
There is also a law specifying how Applicative should relate to Functor:
fmap g x = pure g <*> x
It says that mapping a pure function g over a context x is the same as first injecting g into a context with pure, and then applying it to x with (<*>). In other words, we can decompose fmap into two more atomic operations: injection into a context, and application within a context. Since (<$>) is a synonym for fmap, the above law can also be expressed as:
g <$> x = pure g <*> x.
| Exercises |
|---|
|
Instances
Most of the standard types which are instances of Functor are also instances of Applicative.
Maybe can easily be made an instance of Applicative; writing such an instance is left as an exercise for the reader.
The list type constructor [] can actually be made an instance of Applicative in two ways; essentially, it comes down to whether we want to think of lists as ordered collections of elements, or as contexts representing multiple results of a nondeterministic computation (see Wadler’s How to replace failure by a list of successes).
Let’s first consider the collection point of view. Since there can only be one instance of a given type class for any particular type, one or both of the list instances of Applicative need to be defined for a newtype wrapper; as it happens, the nondeterministic computation instance is the default, and the collection instance is defined in terms of a newtype called ZipList. This instance is:
newtype ZipList a = ZipList { getZipList :: [a] }
instance Applicative ZipList where
pure :: a -> ZipList a
pure = undefined -- exercise
(<*>) :: ZipList (a -> b) -> ZipList a -> ZipList b
(ZipList gs) <*> (ZipList xs) = ZipList (zipWith ($) gs xs)
To apply a list of functions to a list of inputs with (<*>), we just match up the functions and inputs elementwise, and produce a list of the resulting outputs. In other words, we “zip” the lists together with function application, ($); hence the name ZipList.
The other Applicative instance for lists, based on the nondeterministic computation point of view, is:
instance Applicative [] where
pure :: a -> [a]
pure x = [x]
(<*>) :: [a -> b] -> [a] -> [b]
gs <*> xs = [ g x | g <- gs, x <- xs ]
Instead of applying functions to inputs pairwise, we apply each function to all the inputs in turn, and collect all the results in a list.
Now we can write nondeterministic computations in a natural style. To add the numbers 3 and 4 deterministically, we can of course write (+) 3 4. But suppose instead of 3 we have a nondeterministic computation that might result in 2, 3, or 4; then we can write
pure (+) <*> [2,3,4] <*> pure 4
or, more idiomatically,
(+) <$> [2,3,4] <*> pure 4.
There are several other Applicative instances as well:
IOis an instance ofApplicative, and behaves exactly as you would think: to executem1 <*> m2, firstm1is executed, resulting in a functionf, thenm2is executed, resulting in a valuex, and finally the valuef xis returned as the result of executingm1 <*> m2.
((,) a)is anApplicative, as long asais an instance ofMonoid(section Monoid). Theavalues are accumulated in parallel with the computation.
- The
Applicativemodule defines theConsttype constructor; a value of typeConst a bsimply contains ana. This is an instance ofApplicativefor anyMonoid a; this instance becomes especially useful in conjunction with things likeFoldable(section Foldable).
- The
WrappedMonadandWrappedArrownewtypes make any instances ofMonad(section Monad) orArrow(section Arrow) respectively into instances ofApplicative; as we will see when we study those type classes, both are strictly more expressive thanApplicative, in the sense that theApplicativemethods can be implemented in terms of their methods.
| Exercises |
|---|
|
Intuition
McBride and Paterson’s paper introduces the notation to denote function application in a computational context. If each has type for some applicative functor , and has type , then the entire expression has type . You can think of this as applying a function to multiple “effectful” arguments. In this sense, the double bracket notation is a generalization of fmap, which allows us to apply a function to a single argument in a context.
Why do we need Applicative to implement this generalization of fmap? Suppose we use fmap to apply g to the first parameter x1. Then we get something of type f (t2 -> ... t), but now we are stuck: we can’t apply this function-in-a-context to the next argument with fmap. However, this is precisely what (<*>) allows us to do.
This suggests the proper translation of the idealized notation into Haskell, namely
g <$> x1 <*> x2 <*> ... <*> xn,
recalling that Control.Applicative defines (<$>) as convenient infix shorthand for fmap. This is what is meant by an “applicative style”—effectful computations can still be described in terms of function application; the only difference is that we have to use the special operator (<*>) for application instead of simple juxtaposition.
Note that pure allows embedding “non-effectful” arguments in the middle of an idiomatic application, like
g <$> x1 <*> pure x2 <*> x3
which has type f d, given
g :: a -> b -> c -> d
x1 :: f a
x2 :: b
x3 :: f c
The double brackets are commonly known as “idiom brackets”, because they allow writing “idiomatic” function application, that is, function application that looks normal but has some special, non-standard meaning (determined by the particular instance of Applicative being used). Idiom brackets are not supported by GHC, but they are supported by the Strathclyde Haskell Enhancement, a preprocessor which (among many other things) translates idiom brackets into standard uses of (<$>) and (<*>). This can result in much more readable code when making heavy use of Applicative.
In addition, as of GHC 8, the ApplicativeDo extension enables g <$> x1 <*> x2 <*> ... <*> xn to be written in a different style:
do v1 <- x1
v2 <- x2
...
vn <- xn
pure (g v1 v2 ... vn)
See the Further Reading section below as well as the discussion of do-notation in the Monad section for more information.
Utility functions
Control.Applicative provides several utility functions that work generically with any Applicative instance.
liftA :: Applicative f => (a -> b) -> f a -> f b. This should be familiar; of course, it is the same asfmap(and hence also the same as(<$>)), but with a more restrictive type. This probably exists to provide a parallel toliftA2andliftA3, but there is no reason you should ever need to use it.
liftA2 :: Applicative f => (a -> b -> c) -> f a -> f b -> f clifts a 2-argument function to operate in the context of someApplicative. WhenliftA2is fully applied, as inliftA2 f arg1 arg2,it is typically better style to instead usef <$> arg1 <*> arg2. However,liftA2can be useful in situations where it is partially applied. For example, one could define aNuminstance forMaybe Integerby defining(+) = liftA2 (+)and so on.
- There is a
liftA3but noliftAnfor largern.
(*>) :: Applicative f => f a -> f b -> f bsequences the effects of twoApplicativecomputations, but discards the result of the first. For example, ifm1, m2 :: Maybe Int, thenm1 *> m2isNothingwhenever eitherm1orm2isNothing; but if not, it will have the same value asm2.
- Likewise,
(<*) :: Applicative f => f a -> f b -> f asequences the effects of two computations, but keeps only the result of the first, discarding the result of the second. Just as with(<$)and($>), to keep(<*)and(*>)straight, remember that they point towards the values that will be kept.
(<**>) :: Applicative f => f a -> f (a -> b) -> f bis similar to(<*>), but where the first computation produces value(s) which are provided as input to the function(s) produced by the second computation. Note this is not the same asflip (<*>), because the effects are performed in the opposite order. This is possible to observe with anyApplicativeinstance with non-commutative effects, such as the instance for lists:(<**>) [1,2] [(+5),(*10)]produces a different result than(flip (<*>))on the same arguments.
when :: Applicative f => Bool -> f () -> f ()conditionally executes a computation, evaluating to its second argument if the test isTrue, and topure ()if the test isFalse.
unless :: Applicative f => Bool -> f () -> f ()is likewhen, but with the test negated.
- The
guardfunction is for use with instances ofAlternative(an extension ofApplicativeto incorporate the ideas of failure and choice), which is discussed in the section onAlternativeand friends.
| Exercises |
|---|
|
Alternative formulation
An alternative, equivalent formulation of Applicative is given by
class Functor f => Monoidal f where
unit :: f ()
(**) :: f a -> f b -> f (a,b)
∗ In category-theory speak, we say f is a lax monoidal functor because there aren't necessarily functions in the other direction, like f (a, b) -> (f a, f b).
Intuitively, this states that a monoidal functor∗ is one which has some sort of "default shape" and which supports some sort of "combining" operation. pure and (<*>) are equivalent in power to unit and (**) (see the Exercises below). More technically, the idea is that f preserves the "monoidal structure" given by the pairing constructor (,) and unit type (). This can be seen even more clearly if we rewrite the types of unit and (**) as
unit' :: () -> f ()
(**') :: (f a, f b) -> f (a, b)
Furthermore, to deserve the name "monoidal" (see the section on Monoids), instances of Monoidal ought to satisfy the following laws, which seem much more straightforward than the traditional Applicative laws:
∗ In this and the following laws, ≅ refers to isomorphism rather than equality. In particular we consider (x,()) ≅ x ≅ ((),x) and ((x,y),z) ≅ (x,(y,z)).
- Left identity∗:
unit ** v ≅ v
- Right identity:
u ** unit ≅ u
- Associativity:
u ** (v ** w) ≅ (u ** v) ** w
These turn out to be equivalent to the usual Applicative laws. In a category theory setting, one would also require a naturality law:
∗ Here g *** h = \(x,y) -> (g x, h y). See Arrows.
- Naturality:
fmap (g *** h) (u ** v) = fmap g u ** fmap h v
but in the context of Haskell, this is a free theorem.
Much of this section was taken from a blog post by Edward Z. Yang; see his actual post for a bit more information.
| Exercises |
|---|
|
Further reading
McBride and Paterson’s original paper is a treasure-trove of information and examples, as well as some perspectives on the connection between Applicative and category theory. Beginners will find it difficult to make it through the entire paper, but it is extremely well-motivated—even beginners will be able to glean something from reading as far as they are able.
∗ Introduced by an earlier paper that was since superseded by Push-pull functional reactive programming.
Conal Elliott has been one of the biggest proponents of Applicative. For example, the Pan library for functional images and the reactive library for functional reactive programming (FRP) ∗ make key use of it; his blog also contains many examples of Applicative in action. Building on the work of McBride and Paterson, Elliott also built the TypeCompose library, which embodies the observation (among others) that Applicative types are closed under composition; therefore, Applicative instances can often be automatically derived for complex types built out of simpler ones.
Although the Parsec parsing library (paper) was originally designed for use as a monad, in its most common use cases an Applicative instance can be used to great effect; Bryan O’Sullivan’s blog post is a good starting point. If the extra power provided by Monad isn’t needed, it’s usually a good idea to use Applicative instead.
A couple other nice examples of Applicative in action include the ConfigFile and HSQL libraries and the formlets library.
Gershom Bazerman's post contains many insights into applicatives.
The ApplicativeDo extension is described in this wiki page, and in more detail in this Haskell Symposium paper.
Monad
It’s a safe bet that if you’re reading this, you’ve heard of monads—although it’s quite possible you’ve never heard of Applicative before, or Arrow, or even Monoid. Why are monads such a big deal in Haskell? There are several reasons.
- Haskell does, in fact, single out monads for special attention by making them the framework in which to construct I/O operations.
- Haskell also singles out monads for special attention by providing a special syntactic sugar for monadic expressions: the
do-notation. (As of GHC 8,do-notation can be used withApplicativeas well, but the notation is still fundamentally related to monads.) Monadhas been around longer than other abstract models of computation such asApplicativeorArrow.- The more monad tutorials there are, the harder people think monads must be, and the more new monad tutorials are written by people who think they finally “get” monads (the monad tutorial fallacy).
I will let you judge for yourself whether these are good reasons.
In the end, despite all the hoopla, Monad is just another type class. Let’s take a look at its definition.
Definition
As of GHC 7.10, Monad is defined as:
class Applicative m => Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
m >> n = m >>= \_ -> n
fail :: String -> m a
(Prior to GHC 7.10, Applicative was not a superclass of Monad, for historical reasons.)
The Monad type class is exported by the Prelude, along with a few standard instances. However, many utility functions are found in Control.Monad.
Let’s examine the methods in the Monad class one by one. The type of return should look familiar; it’s the same as pure. Indeed, return is pure, but with an unfortunate name. (Unfortunate, since someone coming from an imperative programming background might think that return is like the C or Java keyword of the same name, when in fact the similarities are minimal.) For historical reasons, we still have both names, but they should always denote the same value (although this cannot be enforced). Likewise, (>>) should be the same as (*>) from Applicative. It is possible that return and (>>) may eventually be removed from the Monad class: see the Monad of No Return proposal.
We can see that (>>) is a specialized version of (>>=), with a default implementation given. It is only included in the type class declaration so that specific instances of Monad can override the default implementation of (>>) with a more efficient one, if desired. Also, note that although _ >> n = n would be a type-correct implementation of (>>), it would not correspond to the intended semantics: the intention is that m >> n ignores the result of m, but not its effects.
The fail function is an awful hack that has no place in the Monad class; more on this later.
The only really interesting thing to look at—and what makes Monad strictly more powerful than Applicative—is (>>=), which is often called bind.
We could spend a while talking about the intuition behind (>>=)—and we will. But first, let’s look at some examples.
Instances
Even if you don’t understand the intuition behind the Monad class, you can still create instances of it by just seeing where the types lead you. You may be surprised to find that this actually gets you a long way towards understanding the intuition; at the very least, it will give you some concrete examples to play with as you read more about the Monad class in general. The first few examples are from the standard Prelude; the remaining examples are from the transformers package.
- The simplest possible instance of
MonadisIdentity, which is described in Dan Piponi’s highly recommended blog post on The Trivial Monad. Despite being “trivial”, it is a great introduction to theMonadtype class, and contains some good exercises to get your brain working. - The next simplest instance of
MonadisMaybe. We already know how to writereturn/pureforMaybe. So how do we write(>>=)? Well, let’s think about its type. Specializing forMaybe, we have(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b.
If the first argument to
(>>=)isJust x, then we have something of typea(namely,x), to which we can apply the second argument—resulting in aMaybe b, which is exactly what we wanted. What if the first argument to(>>=)isNothing? In that case, we don’t have anything to which we can apply thea -> Maybe bfunction, so there’s only one thing we can do: yieldNothing. This instance is:instance Monad Maybe where return :: a -> Maybe a return = Just (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b (Just x) >>= g = g x Nothing >>= _ = Nothing
We can already get a bit of intuition as to what is going on here: if we build up a computation by chaining together a bunch of functions with
(>>=), as soon as any one of them fails, the entire computation will fail (becauseNothing >>= fisNothing, no matter whatfis). The entire computation succeeds only if all the constituent functions individually succeed. So theMaybemonad models computations which may fail. - The
Monadinstance for the list constructor[]is similar to itsApplicativeinstance; see the exercise below. - Of course, the
IOconstructor is famously aMonad, but its implementation is somewhat magical, and may in fact differ from compiler to compiler. It is worth emphasizing that theIOmonad is the only monad which is magical. It allows us to build up, in an entirely pure way, values representing possibly effectful computations. The special valuemain, of typeIO (), is taken by the runtime and actually executed, producing actual effects. Every other monad is functionally pure, and requires no special compiler support. We often speak of monadic values as “effectful computations”, but this is because some monads allow us to write code as if it has side effects, when in fact the monad is hiding the plumbing which allows these apparent side effects to be implemented in a functionally pure way. - As mentioned earlier,
((->) e)is known as the reader monad, since it describes computations in which a value of typeeis available as a read-only environment. TheControl.Monad.Readermodule provides theReader e atype, which is just a convenientnewtypewrapper around(e -> a), along with an appropriateMonadinstance and someReader-specific utility functions such asask(retrieve the environment),asks(retrieve a function of the environment), andlocal(run a subcomputation under a different environment). - The
Control.Monad.Writermodule provides theWritermonad, which allows information to be collected as a computation progresses.Writer w ais isomorphic to(a,w), where the output valueais carried along with an annotation or “log” of typew, which must be an instance ofMonoid(see section Monoid); the special functiontellperforms logging. - The
Control.Monad.Statemodule provides theState s atype, anewtypewrapper arounds -> (a,s). Something of typeState s arepresents a stateful computation which produces anabut can access and modify the state of typesalong the way. The module also providesState-specific utility functions such asget(read the current state),gets(read a function of the current state),put(overwrite the state), andmodify(apply a function to the state). - The
Control.Monad.Contmodule provides theContmonad, which represents computations in continuation-passing style. It can be used to suspend and resume computations, and to implement non-local transfers of control, co-routines, other complex control structures—all in a functionally pure way.Conthas been called the “mother of all monads” because of its universal properties.
| Exercises |
|---|
|
Intuition
Let’s look more closely at the type of (>>=). The basic intuition is that it combines two computations into one larger computation. The first argument, m a, is the first computation. However, it would be boring if the second argument were just an m b; then there would be no way for the computations to interact with one another (actually, this is exactly the situation with Applicative). So, the second argument to (>>=) has type a -> m b: a function of this type, given a result of the first computation, can produce a second computation to be run. In other words, x >>= k is a computation which runs x, and then uses the result(s) of x to decide what computation to run second, using the output of the second computation as the result of the entire computation.
∗ Actually, because Haskell allows general recursion, one can recursively construct infinite grammars, and hence Applicative (together with Alternative) is enough to parse any context-sensitive language with a finite alphabet. See Parsing context-sensitive languages with Applicative.
Intuitively, it is this ability to use the output from previous computations to decide what computations to run next that makes Monad more powerful than Applicative. The structure of an Applicative computation is fixed, whereas the structure of a Monad computation can change based on intermediate results. This also means that parsers built using an Applicative interface can only parse context-free languages; in order to parse context-sensitive languages a Monad interface is needed.∗
To see the increased power of Monad from a different point of view, let’s see what happens if we try to implement (>>=) in terms of fmap, pure, and (<*>). We are given a value x of type m a, and a function k of type a -> m b, so the only thing we can do is apply k to x. We can’t apply it directly, of course; we have to use fmap to lift it over the m. But what is the type of fmap k? Well, it’s m a -> m (m b). So after we apply it to x, we are left with something of type m (m b)—but now we are stuck; what we really want is an m b, but there’s no way to get there from here. We can add m’s using pure, but we have no way to collapse multiple m’s into one.
∗ You might hear some people claim that the definition in terms of return, fmap, and join is the “math definition” and the definition in terms of return and (>>=) is something specific to Haskell. In fact, both definitions were known in the mathematics community long before Haskell picked up monads.
This ability to collapse multiple m’s is exactly the ability provided by the function join :: m (m a) -> m a, and it should come as no surprise that an alternative definition of Monad can be given in terms of join:
class Applicative m => Monad'' m where
join :: m (m a) -> m a
In fact, the canonical definition of monads in category theory is in terms of return, fmap, and join (often called , , and in the mathematical literature). Haskell uses an alternative formulation with (>>=) instead of join since it is more convenient to use ∗. However, sometimes it can be easier to think about Monad instances in terms of join, since it is a more “atomic” operation. (For example, join for the list monad is just concat.)
| Exercises |
|---|
|
Utility functions
The Control.Monad module provides a large number of convenient utility functions, all of which can be implemented in terms of the basic Monad operations (return and (>>=) in particular). We have already seen one of them, namely, join. We also mention some other noteworthy ones here; implementing these utility functions oneself is a good exercise. For a more detailed guide to these functions, with commentary and example code, see Henk-Jan van Tuyl’s tour.
liftM :: Monad m => (a -> b) -> m a -> m b. This should be familiar; of course, it is justfmap. The fact that we have bothfmapandliftMis a consequence of the fact that theMonadtype class did not require aFunctorinstance until recently, even though mathematically speaking, every monad is a functor. If you are using GHC 7.10 or newer, you should avoid usingliftMand just usefmapinstead.
ap :: Monad m => m (a -> b) -> m a -> m bshould also be familiar: it is equivalent to(<*>), justifying the claim that theMonadinterface is strictly more powerful thanApplicative. We can make anyMonadinto an instance ofApplicativeby settingpure = returnand(<*>) = ap.
sequence :: Monad m => [m a] -> m [a]takes a list of computations and combines them into one computation which collects a list of their results. It is again something of a historical accident thatsequencehas aMonadconstraint, since it can actually be implemented only in terms ofApplicative(see the exercise at the end of the Utility Functions section for Applicative). Note that the actual type ofsequenceis more general, and works over anyTraversablerather than just lists; see the section onTraversable.
replicateM :: Monad m => Int -> m a -> m [a]is simply a combination ofreplicateandsequence.
mapM :: Monad m => (a -> m b) -> [a] -> m [b]maps its first argument over the second, andsequences the results. TheforMfunction is justmapMwith its arguments reversed; it is calledforMsince it models generalizedforloops: the list[a]provides the loop indices, and the functiona -> m bspecifies the “body” of the loop for each index. Again, these functions actually work over anyTraversable, not just lists, and they can also be defined in terms ofApplicative, notMonad: the analogue ofmapMforApplicativeis calledtraverse.
(=<<) :: Monad m => (a -> m b) -> m a -> m bis just(>>=)with its arguments reversed; sometimes this direction is more convenient since it corresponds more closely to function application.
(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> a -> m cis sort of like function composition, but with an extramon the result type of each function, and the arguments swapped. We’ll have more to say about this operation later. There is also a flipped variant,(<=<).
Many of these functions also have “underscored” variants, such as sequence_ and mapM_; these variants throw away the results of the computations passed to them as arguments, using them only for their side effects.
Other monadic functions which are occasionally useful include filterM, zipWithM, foldM, and forever.
Laws
There are several laws that instances of Monad should satisfy (see also the Monad laws wiki page). The standard presentation is:
return a >>= k = k a
m >>= return = m
m >>= (\x -> k x >>= h) = (m >>= k) >>= h
The first and second laws express the fact that return behaves nicely: if we inject a value a into a monadic context with return, and then bind to k, it is the same as just applying k to a in the first place; if we bind a computation m to return, nothing changes. The third law essentially says that (>>=) is associative, sort of.
∗ I like to pronounce this operator “fish”.
However, the presentation of the above laws, especially the third, is marred by the asymmetry of (>>=). It’s hard to look at the laws and see what they’re really saying. I prefer a much more elegant version of the laws, which is formulated in terms of (>=>) ∗. Recall that (>=>) “composes” two functions of type a -> m b and b -> m c. You can think of something of type a -> m b (roughly) as a function from a to b which may also have some sort of effect in the context corresponding to m. (>=>) lets us compose these “effectful functions”, and we would like to know what properties (>=>) has. The monad laws reformulated in terms of (>=>) are:
return >=> g = g
g >=> return = g
(g >=> h) >=> k = g >=> (h >=> k)
∗ As fans of category theory will note, these laws say precisely that functions of type a -> m b are the arrows of a category with (>=>) as composition! Indeed, this is known as the Kleisli category of the monad m. It will come up again when we discuss Arrows.
Ah, much better! The laws simply state that return is the identity of (>=>), and that (>=>) is associative ∗.
There is also a formulation of the monad laws in terms of fmap, return, and join; for a discussion of this formulation, see the Haskell wikibook page on category theory.
| Exercises |
|---|
|
do notation
Haskell’s special do notation supports an “imperative style” of programming by providing syntactic sugar for chains of monadic expressions. The genesis of the notation lies in realizing that something like a >>= \x -> b >> c >>= \y -> d can be more readably written by putting successive computations on separate lines:
a >>= \x ->
b >>
c >>= \y ->
d
This emphasizes that the overall computation consists of four computations a, b, c, and d, and that x is bound to the result of a, and y is bound to the result of c (b, c, and d are allowed to refer to x, and d is allowed to refer to y as well). From here it is not hard to imagine a nicer notation:
do { x <- a
; b
; y <- c
; d
}
(The curly braces and semicolons may optionally be omitted; the Haskell parser uses layout to determine where they should be inserted.) This discussion should make clear that do notation is just syntactic sugar. In fact, do blocks are recursively translated into monad operations (almost) like this:
do e → e
do { e; stmts } → e >> do { stmts }
do { v <- e; stmts } → e >>= \v -> do { stmts }
do { let decls; stmts} → let decls in do { stmts }
This is not quite the whole story, since v might be a pattern instead of a variable. For example, one can write
do (x:xs) <- foo
bar x
but what happens if foo is an empty list? Well, remember that ugly fail function in the Monad type class declaration? That’s what happens. See section 3.14 of the Haskell Report for the full details. See also the discussion of MonadPlus and MonadZero in the section on other monoidal classes.
A final note on intuition: do notation plays very strongly to the “computational context” point of view rather than the “container” point of view, since the binding notation x <- m is suggestive of “extracting” a single x from m and doing something with it. But m may represent some sort of a container, such as a list or a tree; the meaning of x <- m is entirely dependent on the implementation of (>>=). For example, if m is a list, x <- m actually means that x will take on each value from the list in turn.
Sometimes, the full power of Monad is not needed to desugar do-notation. For example,
do x <- foo1
y <- foo2
z <- foo3
return (g x y z)
would normally be desugared to foo1 >>= \x -> foo2 >>= \y -> foo3 >>= \z -> return (g x y z), but this is equivalent to g <$> foo1 <*> foo2 <*> foo3. With the ApplicativeDo extension enabled (as of GHC 8.0), GHC tries hard to desugar do-blocks using Applicative operations wherever possible. This can sometimes lead to efficiency gains, even for types which also have Monad instances, since in general Applicative computations may be run in parallel, whereas monadic ones may not. For example, consider
g :: Int -> Int -> M Int
-- These could be expensive
bar, baz :: M Int
foo :: M Int
foo = do
x <- bar
y <- baz
g x y
foo definitely depends on the Monad instance of M, since the effects generated by the whole computation may depend (via g) on the Int outputs of bar and baz. Nonetheless, with ApplicativeDo enabled, foo can be desugared as
join (g <$> bar <*> baz)
which may allow bar and baz to be computed in parallel, since they at least do not depend on each other.
The ApplicativeDo extension is described in this wiki page, and in more detail in this Haskell Symposium paper.
Further reading
Philip Wadler was the first to propose using monads to structure functional programs. His paper is still a readable introduction to the subject.
∗ All About Monads, Monads as containers, Understanding monads, The Monadic Way, You Could Have Invented Monads! (And Maybe You Already Have.), there’s a monster in my Haskell!, Understanding Monads. For real., Monads in 15 minutes: Backtracking and Maybe, Monads as computation, Practical Monads
There are, of course, numerous monad tutorials of varying quality ∗.
A few of the best include Cale Gibbard’s Monads as containers and Monads as computation; Jeff Newbern’s All About Monads, a comprehensive guide with lots of examples; and Dan Piponi’s You Could Have Invented Monads!, which features great exercises. If you just want to know how to use IO, you could consult the Introduction to IO. Even this is just a sampling; the monad tutorials timeline is a more complete list. (All these monad tutorials have prompted parodies like think of a monad ... as well as other kinds of backlash like Monads! (and Why Monad Tutorials Are All Awful) or Abstraction, intuition, and the “monad tutorial fallacy”.)
Other good monad references which are not necessarily tutorials include Henk-Jan van Tuyl’s tour of the functions in Control.Monad, Dan Piponi’s field guide, Tim Newsham’s What’s a Monad?, and Chris Smith's excellent article Why Do Monads Matter?. There are also many blog posts which have been written on various aspects of monads; a collection of links can be found under Blog articles/Monads.
For help constructing monads from scratch, and for obtaining a "deep embedding" of monad operations suitable for use in, say, compiling a domain-specific language, see Apfelmus's operational package.
One of the quirks of the Monad class and the Haskell type system is that it is not possible to straightforwardly declare Monad instances for types which require a class constraint on their data, even if they are monads from a mathematical point of view. For example, Data.Set requires an Ord constraint on its data, so it cannot be easily made an instance of Monad. A solution to this problem was first described by Eric Kidd, and later made into a library named rmonad by Ganesh Sittampalam and Peter Gavin.
There are many good reasons for eschewing do notation; some have gone so far as to consider it harmful.
Monads can be generalized in various ways; for an exposition of one possibility, see Robert Atkey’s paper on parameterized monads, or Dan Piponi’s Beyond Monads.
For the categorically inclined, monads can be viewed as monoids (From Monoids to Monads) and also as closure operators (Triples and Closure). Derek Elkins’ article in issue 13 of the Monad.Reader contains an exposition of the category-theoretic underpinnings of some of the standard Monad instances, such as State and Cont. Jonathan Hill and Keith Clarke have an early paper explaining the connection between monads as they arise in category theory and as used in functional programming. There is also a web page by Oleg Kiselyov explaining the history of the IO monad.
Links to many more research papers related to monads can be found under Research papers/Monads and arrows.
MonadFail
Some monads support a notion of failure, without necessarily supporting the notion of recovery suggested by MonadPlus, and possibly including a primitive error reporting mechanism. This notion is expressed by the relatively unprincipled MonadFail. When the MonadFailDesugaring language extension is enabled, the fail method from MonadFail is used for pattern match failure in do bindings rather than the traditional fail method of the Monad class. This language change is being implemented because there are many monads, such as Reader, State, Writer, RWST, and Cont that simply do not support a legitimate fail method.
See the MonadFail proposal for more information.
Definition
class Monad m => MonadFail m where
fail :: String -> m a
Law
fail s >>= m = fail s
Monad transformers
One would often like to be able to combine two monads into one: for example, to have stateful, nondeterministic computations (State + []), or computations which may fail and can consult a read-only environment (Maybe + Reader), and so on. Unfortunately, monads do not compose as nicely as applicative functors (yet another reason to use Applicative if you don’t need the full power that Monad provides), but some monads can be combined in certain ways.
Standard monad transformers
The transformers library provides a number of standard monad transformers. Each monad transformer adds a particular capability/feature/effect to any existing monad.
IdentityTis the identity transformer, which maps a monad to (something isomorphic to) itself. This may seem useless at first glance, but it is useful for the same reason that theidfunction is useful -- it can be passed as an argument to things which are parameterized over an arbitrary monad transformer, when you do not actually want any extra capabilities.StateTadds a read-write state.ReaderTadds a read-only environment.WriterTadds a write-only log.RWSTconveniently combinesReaderT,WriterT, andStateTinto one.MaybeTadds the possibility of failure.ErrorTadds the possibility of failure with an arbitrary type to represent errors.ListTadds non-determinism (however, see the discussion ofListTbelow).ContTadds continuation handling.
For example, StateT s Maybe is an instance of Monad; computations of type StateT s Maybe a may fail, and have access to a mutable state of type s. Monad transformers can be multiply stacked. One thing to keep in mind while using monad transformers is that the order of composition matters. For example, when a StateT s Maybe a computation fails, the state ceases being updated (indeed, it simply disappears); on the other hand, the state of a MaybeT (State s) a computation may continue to be modified even after the computation has "failed". This may seem backwards, but it is correct. Monad transformers build composite monads “inside out”; MaybeT (State s) a is isomorphic to s -> (Maybe a, s). (Lambdabot has an indispensable @unmtl command which you can use to “unpack” a monad transformer stack in this way.)
Intuitively, the monads become "more fundamental" the further inside the stack you get, and the effects of inner monads "have precedence" over the effects of outer ones. Of course, this is just handwaving, and if you are unsure of the proper order for some monads you wish to combine, there is no substitute for using @unmtl or simply trying out the various options.
Definition and laws
All monad transformers should implement the MonadTrans type class, defined in Control.Monad.Trans.Class:
class MonadTrans t where
lift :: Monad m => m a -> t m a
It allows arbitrary computations in the base monad m to be “lifted” into computations in the transformed monad t m. (Note that type application associates to the left, just like function application, so t m a = (t m) a.)
lift must satisfy the laws
lift . return = return
lift (m >>= f) = lift m >>= (lift . f)
which intuitively state that lift transforms m a computations into t m a computations in a "sensible" way, which sends the return and (>>=) of m to the return and (>>=) of t m.
| Exercises |
|---|
|
Transformer type classes and "capability" style
∗ The only problem with this scheme is the quadratic number of instances required as the number of standard monad transformers grows—but as the current set of standard monad transformers seems adequate for most common use cases, this may not be that big of a deal.
There are also type classes (provided by the mtl package) for the operations of each transformer. For example, the MonadState type class provides the state-specific methods get and put, allowing you to conveniently use these methods not only with State, but with any monad which is an instance of MonadState—including MaybeT (State s), StateT s (ReaderT r IO), and so on. Similar type classes exist for Reader, Writer, Cont, IO, and others ∗.
These type classes serve two purposes. First, they get rid of (most of) the need for explicitly using lift, giving a type-directed way to automatically determine the right number of calls to lift. Simply writing put will be automatically translated into lift . put, lift . lift . put, or something similar depending on what concrete monad stack you are using.
Second, they give you more flexibility to switch between different concrete monad stacks. For example, if you are writing a state-based algorithm, don't write
foo :: State Int Char
foo = modify (*2) >> return 'x'
but rather
foo :: MonadState Int m => m Char
foo = modify (*2) >> return 'x'
Now, if somewhere down the line you realize you need to introduce the possibility of failure, you might switch from State Int to MaybeT (State Int). The type of the first version of foo would need to be modified to reflect this change, but the second version of foo can still be used as-is.
However, this sort of "capability-based" style (e.g. specifying that foo works for any monad with the "state capability") quickly runs into problems when you try to naively scale it up: for example, what if you need to maintain two independent states? A framework for solving this and related problems is described by Schrijvers and Olivera (Monads, zippers and views: virtualizing the monad stack, ICFP 2011) and is implemented in the Monatron package.
Composing monads
Is the composition of two monads always a monad? As hinted previously, the answer is no.
Since Applicative functors are closed under composition, the problem must lie with join. Indeed, suppose m and n are arbitrary monads; to make a monad out of their composition we would need to be able to implement
join :: m (n (m (n a))) -> m (n a)
but it is not clear how this could be done in general. The join method for m is no help, because the two occurrences of m are not next to each other (and likewise for n).
However, one situation in which it can be done is if n distributes over m, that is, if there is a function
distrib :: n (m a) -> m (n a)
satisfying certain laws. See Jones and Duponcheel (Composing Monads); see also the section on Traversable.
For a much more in-depth discussion and analysis of the failure of monads to be closed under composition, see this question on StackOverflow.
| Exercises |
|---|
|
Further reading
Much of the monad transformer library (originally mtl, now split between mtl and transformers), including the Reader, Writer, State, and other monads, as well as the monad transformer framework itself, was inspired by Mark Jones’ classic paper Functional Programming with Overloading and Higher-Order Polymorphism. It’s still very much worth a read—and highly readable—after almost fifteen years.
See Edward Kmett's mailing list message for a description of the history and relationships among monad transformer packages (mtl, transformers, monads-fd, monads-tf).
There are two excellent references on monad transformers. Martin Grabmüller’s Monad Transformers Step by Step is a thorough description, with running examples, of how to use monad transformers to elegantly build up computations with various effects. Cale Gibbard’s article on how to use monad transformers is more practical, describing how to structure code using monad transformers to make writing it as painless as possible. Another good starting place for learning about monad transformers is a blog post by Dan Piponi.
The ListT transformer from the transformers package comes with the caveat that ListT m is only a monad when m is commutative, that is, when ma >>= \a -> mb >>= \b -> foo is equivalent to mb >>= \b -> ma >>= \a -> foo (i.e. the order of m's effects does not matter). For one explanation why, see Dan Piponi's blog post "Why isn't ListT [] a monad". For more examples, as well as a design for a version of ListT which does not have this problem, see ListT done right.
There is an alternative way to compose monads, using coproducts, as described by Lüth and Ghani. This method is interesting but has not (yet?) seen widespread use. For a more recent alternative, see Kiselyov et al's Extensible Effects: An Alternative to Monad Transformers.
MonadFix
Note: MonadFix is included here for completeness (and because it is interesting) but seems not to be used much. Skipping this section on a first read-through is perfectly OK (and perhaps even recommended).
do rec notation
The MonadFix class describes monads which support the special fixpoint operation mfix :: (a -> m a) -> m a, which allows the output of monadic computations to be defined via (effectful) recursion. This is supported in GHC by a special “recursive do” notation, enabled by the -XRecursiveDo flag. Within a do block, one may have a nested rec block, like so:
do { x <- foo
; rec { y <- baz
; z <- bar
; bob
}
; w <- frob
}
Normally (if we had do in place of rec in the above example), y would be in scope in bar and bob but not in baz, and z would be in scope only in bob. With the rec, however, y and z are both in scope in all three of baz, bar, and bob. A rec block is analogous to a let block such as
let { y = baz
; z = bar
}
in bob
because, in Haskell, every variable bound in a let-block is in scope throughout the entire block. (From this point of view, Haskell's normal do blocks are analogous to Scheme's let* construct.)
What could such a feature be used for? One of the motivating examples given in the original paper describing MonadFix (see below) is encoding circuit descriptions. A line in a do-block such as
x <- gate y z
describes a gate whose input wires are labeled y and z and whose output wire is labeled x. Many (most?) useful circuits, however, involve some sort of feedback loop, making them impossible to write in a normal do-block (since some wire would have to be mentioned as an input before being listed as an output). Using a rec block solves this problem.
Examples and intuition
Of course, not every monad supports such recursive binding. However, as mentioned above, it suffices to have an implementation of mfix :: (a -> m a) -> m a, satisfying a few laws. Let's try implementing mfix for the Maybe monad. That is, we want to implement a function
maybeFix :: (a -> Maybe a) -> Maybe a
∗ Actually, fix is implemented slightly differently for efficiency reasons; but the given definition is equivalent and simpler for the present purpose.
Let's think for a moment about the implementation ∗ of the non-monadic fix :: (a -> a) -> a:
fix f = f (fix f)
Inspired by fix, our first attempt at implementing maybeFix might be something like
maybeFix :: (a -> Maybe a) -> Maybe a
maybeFix f = maybeFix f >>= f
This has the right type. However, something seems wrong: there is nothing in particular here about Maybe; maybeFix actually has the more general type Monad m => (a -> m a) -> m a. But didn't we just say that not all monads support mfix?
The answer is that although this implementation of maybeFix has the right type, it does not have the intended semantics. If we think about how (>>=) works for the Maybe monad (by pattern-matching on its first argument to see whether it is Nothing or Just) we can see that this definition of maybeFix is completely useless: it will just recurse infinitely, trying to decide whether it is going to return Nothing or Just, without ever even so much as a glance in the direction of f.
The trick is to simply assume that maybeFix will return Just, and get on with life!
maybeFix :: (a -> Maybe a) -> Maybe a
maybeFix f = ma
where ma = f (fromJust ma)
This says that the result of maybeFix is ma, and assuming that ma = Just x, it is defined (recursively) to be equal to f x.
Why is this OK? Isn't fromJust almost as bad as unsafePerformIO? Well, usually, yes. This is just about the only situation in which it is justified! The interesting thing to note is that maybeFix will never crash -- although it may, of course, fail to terminate. The only way we could get a crash is if we try to evaluate fromJust ma when we know that ma = Nothing. But how could we know ma = Nothing? Since ma is defined as f (fromJust ma), it must be that this expression has already been evaluated to Nothing -- in which case there is no reason for us to be evaluating fromJust ma in the first place!
To see this from another point of view, we can consider three possibilities. First, if f outputs Nothing without looking at its argument, then maybeFix f clearly returns Nothing. Second, if f always outputs Just x, where x depends on its argument, then the recursion can proceed usefully: fromJust ma will be able to evaluate to x, thus feeding f's output back to it as input. Third, if f tries to use its argument to decide whether to output Just or Nothing, then maybeFix f will not terminate: evaluating f's argument requires evaluating ma to see whether it is Just, which requires evaluating f (fromJust ma), which requires evaluating ma, ... and so on.
There are also instances of MonadFix for lists (which works analogously to the instance for Maybe), for ST, and for IO. The instance for IO is particularly amusing: it creates a new (empty) MVar, immediately reads its contents using unsafeInterleaveIO (which delays the actual reading lazily until the value is needed), uses the contents of the MVar to compute a new value, which it then writes back into the MVar. It almost seems, spookily, that mfix is sending a value back in time to itself through the MVar -- though of course what is really going on is that the reading is delayed just long enough (via unsafeInterleaveIO) to get the process bootstrapped.
| Exercises |
|---|
|
mdo syntax
The example at the start of this section can also be written
mdo { x <- foo
; y <- baz
; z <- bar
; bob
; w <- frob
}
which will be translated into the original example (assuming that, say, bar and bob refer to y. The difference is that mdo will analyze the code in order to find minimal recursive blocks, which will be placed in rec blocks, whereas rec blocks desugar directly into calls to mfix without any further analysis.
Further reading
For more information (such as the precise desugaring rules for rec blocks), see Levent Erkök and John Launchbury's 2002 Haskell workshop paper, A Recursive do for Haskell, or for full details, Levent Erkök’s thesis, Value Recursion in Monadic Computations. (Note, while reading, that MonadFix used to be called MonadRec.) You can also read the GHC user manual section on recursive do-notation.
Semigroup
A semigroup is a set together with a binary operation which combines elements from . The operator is required to be associative (that is, , for any which are elements of ).
For example, the natural numbers under addition form a semigroup: the sum of any two natural numbers is a natural number, and for any natural numbers , , and . The integers under multiplication also form a semigroup, as do the integers (or rationals, or reals) under or , Boolean values under conjunction and disjunction, lists under concatenation, functions from a set to itself under composition ... Semigroups show up all over the place, once you know to look for them.
Definition
As of version 4.9 of the base package (which comes with GHC 8.0), semigroups are defined in the Data.Semigroup module. (If you are working with a previous version of base, or want to write a library that supports previous versions of base, you can use the semigroups package.)
The definition of the Semigroup type class (haddock) is as follows:
class Semigroup a where
(<>) :: a -> a -> a
sconcat :: NonEmpty a -> a
sconcat (a :| as) = go a as where
go b (c:cs) = b <> go c cs
go b [] = b
stimes :: Integral b => b -> a -> a
stimes = ...
The really important method is (<>), representing the associative binary operation. The other two methods have default implementations in terms of (<>), and are included in the type class in case some instances can give more efficient implementations than the default.
sconcat reduces a nonempty list using (<>). For most instances, this is the same as foldr1 (<>), but it can be constant-time for idempotent semigroups.
stimes n is equivalent to (but sometimes considerably more efficient than) sconcat . replicate n. Its default definition uses multiplication by doubling (also known as exponentiation by squaring). For many semigroups, this is an important optimization; for some, such as lists, it is terrible and must be overridden.
See the haddock documentation for more information on sconcat and stimes.
Laws
The only law is that (<>) must be associative:
(x <> y) <> z = x <> (y <> z)
Monoid
Many semigroups have a special element for which the binary operation is the identity, that is, for every element . Such a semigroup-with-identity-element is called a monoid.
Definition
The definition of the Monoid type class (defined in
Data.Monoid; haddock) is:
class Monoid a where
mempty :: a
mappend :: a -> a -> a
mconcat :: [a] -> a
mconcat = foldr mappend mempty
The mempty value specifies the identity element of the monoid, and mappend
is the binary operation. The default definition for mconcat
“reduces” a list of elements by combining them all with mappend,
using a right fold. It is only in the Monoid class so that specific
instances have the option of providing an alternative, more efficient
implementation; usually, you can safely ignore mconcat when creating
a Monoid instance, since its default definition will work just fine.
The Monoid methods are rather unfortunately named; they are inspired
by the list instance of Monoid, where indeed mempty = [] and mappend = (++), but this is misleading since many
monoids have little to do with appending (see these Comments from OCaml Hacker Brian Hurt on the Haskell-cafe mailing list). The situation is made somewhat better by (<>), which is provided as an alias for mappend.
Note that the (<>) alias for mappend conflicts with the Semigroup method of the same name. For this reason, Data.Semigroup re-exports much of Data.Monoid; to use semigroups and monoids together, just import Data.Semigroup, and make sure all your types have both Semigroup and Monoid instances (and that (<>) = mappend).
Laws
Of course, every Monoid instance should actually be a monoid in the
mathematical sense, which implies these laws:
mempty `mappend` x = x
x `mappend` mempty = x
(x `mappend` y) `mappend` z = x `mappend` (y `mappend` z)
Instances
There are quite a few interesting Monoid instances defined in Data.Monoid.
[a]is aMonoid, withmempty = []andmappend = (++). It is not hard to check that(x ++ y) ++ z = x ++ (y ++ z)for any listsx,y, andz, and that the empty list is the identity:[] ++ x = x ++ [] = x.- As noted previously, we can make a monoid out of any numeric type under either addition or multiplication. However, since we can’t have two instances for the same type,
Data.Monoidprovides twonewtypewrappers,SumandProduct, with appropriateMonoidinstances.> getSum (mconcat . map Sum $ [1..5]) 15 > getProduct (mconcat . map Product $ [1..5]) 120
This example code is silly, of course; we could just write
sum [1..5]andproduct [1..5]. Nevertheless, these instances are useful in more generalized settings, as we will see in the section onFoldable. AnyandAllarenewtypewrappers providingMonoidinstances forBool(under disjunction and conjunction, respectively).- There are three instances for
Maybe: a basic instance which lifts aMonoidinstance forato an instance forMaybe a, and twonewtypewrappersFirstandLastfor whichmappendselects the first (respectively last) non-Nothingitem. Endo ais a newtype wrapper for functionsa -> a, which form a monoid under composition.- There are several ways to “lift”
Monoidinstances to instances with additional structure. We have already seen that an instance foracan be lifted to an instance forMaybe a. There are also tuple instances: ifaandbare instances ofMonoid, then so is(a,b), using the monoid operations foraandbin the obvious pairwise manner. Finally, ifais aMonoid, then so is the function typee -> afor anye; in particular,g `mappend` his the function which applies bothgandhto its argument and then combines the results using the underlyingMonoidinstance fora. This can be quite useful and elegant (see example). - The type
Ordering = LT | EQ | GTis aMonoid, defined in such a way thatmconcat (zipWith compare xs ys)computes the lexicographic ordering ofxsandys(ifxsandyshave the same length). In particular,mempty = EQ, andmappendevaluates to its leftmost non-EQargument (orEQif both arguments areEQ). This can be used together with the function instance ofMonoidto do some clever things (example). - There are also
Monoidinstances for several standard data structures in the containers library (haddock), includingMap,Set, andSequence.
Monoid is also used to enable several other type class instances.
As noted previously, we can use Monoid to make ((,) e) an instance of Applicative:
instance Monoid e => Applicative ((,) e) where
pure :: Monoid e => a -> (e,a)
pure x = (mempty, x)
(<*>) :: Monoid e => (e,a -> b) -> (e,a) -> (e,b)
(u, f) <*> (v, x) = (u `mappend` v, f x)
Monoid can be similarly used to make ((,) e) an instance of Monad as well; this is known as the writer monad. As we’ve already seen, Writer and WriterT are a newtype wrapper and transformer for this monad, respectively.
Monoid also plays a key role in the Foldable type class (see section Foldable).
Further reading
Monoids got a fair bit of attention in 2009, when
a blog post by Brian Hurt
complained about the fact that the names of many Haskell type classes
(Monoid in particular) are taken from abstract mathematics. This
resulted in a long Haskell-cafe thread
arguing the point and discussing monoids in general.
∗ May its name live forever.
However, this was quickly followed by several blog posts about
Monoid ∗. First, Dan Piponi
wrote a great introductory post, Haskell Monoids and their Uses. This was quickly followed by
Heinrich Apfelmus’ Monoids and Finger Trees, an accessible exposition of
Hinze and Paterson’s classic paper on 2-3 finger trees, which makes very clever
use of Monoid to implement an elegant and generic data structure.
Dan Piponi then wrote two fascinating articles about using Monoids
(and finger trees): Fast Incremental Regular Expressions and Beyond Regular Expressions
In a similar vein, David Place’s article on improving Data.Map in
order to compute incremental folds (see the Monad Reader issue 11)
is also a
good example of using Monoid to generalize a data structure.
Some other interesting examples of Monoid use include building elegant list sorting combinators, collecting unstructured information, combining probability distributions, and a brilliant series of posts by Chung-Chieh Shan and Dylan Thurston using Monoids to elegantly solve a difficult combinatorial puzzle (followed by part 2, part 3, part 4).
As unlikely as it sounds, monads can actually be viewed as a sort of
monoid, with join playing the role of the binary operation and
return the role of the identity; see Dan Piponi’s blog post.
Failure and choice: Alternative, MonadPlus, ArrowPlus
Several classes (Applicative, Monad, Arrow) have "monoidal" subclasses, intended to model computations that support "failure" and "choice" (in some appropriate sense).
Definition
The Alternative type class (haddock)
is for Applicative functors which also have
a monoid structure:
class Applicative f => Alternative f where
empty :: f a
(<|>) :: f a -> f a -> f a
some :: f a -> f [a]
many :: f a -> f [a]
The basic intuition is that empty represents some sort of "failure", and (<|>) represents a choice between alternatives. (However, this intuition does not fully capture the nuance possible; see the section on Laws below.) Of course, (<|>) should be associative and empty should be the identity element for it.
Instances of Alternative must implement empty and (<|>); some and many have default implementations but are included in the class since specialized implementations may be more efficient than the default.
The default definitions of some and many are essentially given by
some v = (:) <$> v <*> many v
many v = some v <|> pure []
(though for some reason, in actual fact they are not defined via mutual recursion). The intuition is that both keep running v, collecting its results into a list, until it fails; some v requires v to succeed at least once, whereas many v does not require it to succeed at all. That is, many represents 0 or more repetitions of v, whereas some represents 1 or more repetitions. Note that some and many do not make sense for all instances of Alternative; they are discussed further below.
Likewise, MonadPlus (haddock)
is for Monads with a monoid structure:
class Monad m => MonadPlus m where
mzero :: m a
mplus :: m a -> m a -> m a
Finally, ArrowZero and ArrowPlus (haddock)
represent Arrows (see below) with a
monoid structure:
class Arrow arr => ArrowZero arr where
zeroArrow :: b `arr` c
class ArrowZero arr => ArrowPlus arr where
(<+>) :: (b `arr` c) -> (b `arr` c) -> (b `arr` c)
Instances
Although this document typically discusses laws before presenting example instances, for Alternative and friends it is worth doing things the other way around, because there is some controversy over the laws and it helps to have some concrete examples in mind when discussing them. We mostly focus on Alternative in this section and the next; now that Applicative is a superclass of Monad, there is little reason to use MonadPlus any longer, and ArrowPlus is rather obscure.
Maybeis an instance ofAlternative, whereemptyisNothingand the choice operator(<|>)results in its first argument when it isJust, and otherwise results in its second argument. Hence folding over a list ofMaybewith(<|>)(which can be done withasumfromData.Foldable) results in the first non-Nothingvalue in the list (orNothingif there are none).
[]is an instance, withemptygiven by the empty list, and(<|>)equal to(++). It is worth pointing out that this is identical to theMonoidinstance for[a], whereas theAlternativeandMonoidinstances forMaybeare different: theMonoidinstance forMaybe arequires aMonoidinstance fora, and monoidally combines the contained values when presented with twoJusts.
Let's think about the behavior of some and many for Maybe and []. For Maybe, we have some Nothing = (:) <$> Nothing <*> many Nothing = Nothing <*> many Nothing = Nothing. Hence we also have many Nothing = some Nothing <|> pure [] = Nothing <|> pure [] = pure [] = Just []. Boring. But what about applying some and many to Just? In fact, some (Just a) and many (Just a) are both bottom! The problem is that since Just a is always "successful", the recursion will never terminate. In theory the result "should be" the infinite list [a,a,a,...] but it cannot even start producing any elements of this list, because there is no way for the (<*>) operator to yield any output until it knows that the result of the call to many will be Just.
You can work out the behavior for [] yourself, but it ends up being quite similar: some and many yield boring results when applied to the empty list, and yield bottom when applied to any non-empty list.
In the end, some and many really only make sense when used with some sort of "stateful" Applicative instance, for which an action v, when run multiple times, can succeed some finite number of times and then fail. For example, parsers have this behavior, and indeed, parsers were the original motivating example for the some and many methods; more on this below.
- Since GHC 8.0 (that is,
base-4.9), there is an instance ofAlternativeforIO.emptythrows an I/O exception, and(<|>)works by first running its left-hand argument; if the left-hand argument throws an I/O exception,(<|>)catches the exception and then calls its second argument. (Note that other types of exceptions are not caught.) There are other, much better ways to handle I/O errors, but this is a quick and dirty way that may work for simple, one-off programs, such as expressions typed at the GHCi prompt. For example, if you want to read the contents of a file but use some default contents in case the file does not exist, you can just writereadFile "somefile.txt" <|> return "default file contents".
Concurrentlyfrom theasyncpackage has anAlternativeinstance, for whichc1 <|> c2racesc1andc2in parallel, and returns the result of whichever finishes first.emptycorresponds to the action that runs forever without returning a value.
- Practically any parser type (e.g. from
parsec,megaparsec,trifecta, ...) has anAlternativeinstance, whereemptyis an unconditional parse failure, and(<|>)is left-biased choice. That is,p1 <|> p2first tries parsing withp1, and ifp1fails then it triesp2instead.
some and many work particularly well with parser types having an Applicative instance: if p is a parser, then some p parses one or more consecutive occurrences of p (i.e. it will parse as many occurrences of p as possible and then stop), and many p parses zero or more occurrences.
Laws
Of course, instances of Alternative should satisfy the monoid laws
empty <|> x = x
x <|> empty = x
(x <|> y) <|> z = x <|> (y <|> z)
The documentation for some and many states that they should be the "least solution" (i.e. least in the definedness partial order) to their characterizing, mutually recursive default definitions. However, this is controversial, and probably wasn't really thought out very carefully.
Since Alternative is a subclass of Applicative, a natural question is, "how should empty and (<|>) interact with (<*>) and pure?"
Almost everyone agrees on the left zero law (though see the discussion of the right zero law below):
empty <*> f = empty
After this is where it starts to get a bit hairy though. It turns out there are several other laws one might imagine adding, and different instances satisfy different laws.
- Right Zero:
Another obvious law would be
f <*> empty = empty
This law is satisfied by most instances; however, it is not satisfied by
IO. Once the effects infhave been executed, there is no way to roll them back if we later encounter an exception. Now consider theBackwardsapplicative transformer from thetransformerspackage. IffisApplicative, then so isBackwards f; it works the same way but performs the actions of the arguments to(<*>)in the reverse order. There is also an instanceAlternative f => Alternative (Backwards f). If somef(such asIO) satisfies left zero but not right zero, thenBackwards fsatisfies right zero but not left zero! So even the left zero law is suspect. The point is that given the existence ofBackwardswe cannot privilege one direction or the other.
- Left Distribution:
(a <|> b) <*> c = (a <*> c) <|> (b <*> c)
This distributivity law is satisfied by
[]andMaybe, as you may verify. However, it is not satisfied byIOor most parsers. The reason is thataandbcan have effects which influence execution ofc, and the left-hand side may end up failing where the right-hand side succeeds.For example, consider
IO, and suppose thataalways executes successfully, butcthrows an I/O exception afterahas run. Concretely, say,amight ensure that a certain file does not exist (deleting it if it does exist or doing nothing if it does not), and thenctries to read that file. In that case(a <|> b) <*> cwill first delete the file, ignoringbsinceais successful, and then throw an exception whenctries to read the file. On the other hand,bmight ensure that the same file in question does exist. In that case(a <*> c) <|> (b <*> c)would succeed: after(a <*> c)throws an exception, it would be caught by(<|>), and then(b <*> c)would be tried.This law does not hold for parsers for a similar reason:
(a <|> b) <*> chas to "commit" to parsing withaorbbefore runningc, whereas(a <*> c) <|> (b <*> c)allows backtracking ifa <*> cfails. In the particular case thatasucceeds butcfails afterabut not afterb, these may give different results. For example, supposeaandcboth expect to see two asterisks, butbexpects to see only one. If there are only three asterisks in the input,b <*> cwill be successful whereasa <*> cwill not.
- Right Distribution:
a <*> (b <|> c) = (a <*> b) <|> (a <*> c)
This law is not satisfied by very many instances, but it's still worth discussing. In particular the law is still satisfied by
Maybe. However, it is not satisfied by, for example, lists. The problem is that the results come out in a different order. For example, supposea = [(+1), (*10)],b = [2], andc = [3]. Then the left-hand side yields[3,4,20,30], whereas the right-hand side is[3,20,4,30].IOdoes not satisfy it either, since, for example,amay succeed only the second time it is executed. Parsers, on the other hand, may or may not satisfy this law, depending on how they handle backtracking. Parsers for which(<|>)by itself does full backtracking will satisfy the law; but for many parser combinator libraries this is not the case, for efficiency reasons. For example, parsec fails this law: ifasucceeds while consuming some input, and afterwardsbfails without consuming any input, then the left-hand side may succeed while the right-hand side fails: after(a <*> b)fails, the right-hand side tries to re-runawithout backtracking over the input the originalaconsumed.
- Left Catch:
(pure a) <|> x = pure a
Intuitively, this law states that
pureshould always represent a "successful" computation. It is satisfied byMaybe,IO, and parsers. However, it is not satisfied by lists, since lists collect all possible results: it corresponds to[a] ++ x == [a]which is obviously false.
This, then, is the situation: we have a lot of instances of Alternative (and MonadPlus), with each instance satisfying some subset of these laws. Moreover, it's not always the same subset, so there is no obvious "default" set of laws to choose. For now at least, we just have to live with the situation. When using a particular instance of Alternative or MonadPlus, it's worth thinking carefully about which laws it satisfies.
Utility functions
There are a few Alternative-specific utility functions worth mentioning:
- checks the given condition, and evaluates to
guard :: Alternative f => Bool -> f ()
pure ()if the condition holds, andemptyif not. This can be used to create a conditional failure point in the middle of a computation, where the computation only proceeds if a certain condition holds.
- reifies potential failure into the
optional :: Alternative f => f a -> f (Maybe a)
Maybetype: that is,optional xis a computation which always succeeds, returningNothingifxfails andJust aifxsuccessfully results ina. It is useful, for example, in the context of parsers, where it corresponds to a production which can occur zero or one times.
Further reading
There used to be a type class called MonadZero containing only
mzero, representing monads with failure. The do-notation requires
some notion of failure to deal with failing pattern matches.
Unfortunately, MonadZero was scrapped in favor of adding the fail
method to the Monad class. If we are lucky, someday MonadZero will
be restored, and fail will be banished to the bit bucket where it
belongs (see MonadPlus reform proposal). The idea is that any
do-block which uses pattern matching (and hence may fail) would require
a MonadZero constraint; otherwise, only a Monad constraint would be
required.
A great introduction to the MonadPlus type class, with interesting examples of its use, is Doug Auclair’s MonadPlus: What a Super Monad! in the Monad.Reader issue 11.
Another interesting use of MonadPlus can be found in Christiansen et al, All Sorts of Permutations, from ICFP 2016.
The logict package defines a type with prominent Alternative and MonadPlus instances that can be used to efficiently enumerate possibilities subject to constraints, i.e. logic programming; it's like the list monad on steroids.
Foldable
The Foldable class, defined in the Data.Foldable
module (haddock), abstracts over containers which can be
“folded” into a summary value. This allows such folding operations
to be written in a container-agnostic way.
Definition
The definition of the Foldable type class is:
class Foldable t where
fold :: Monoid m => t m -> m
foldMap :: Monoid m => (a -> m) -> t a -> m
foldr :: (a -> b -> b) -> b -> t a -> b
foldr' :: (a -> b -> b) -> b -> t a -> b
foldl :: (b -> a -> b) -> b -> t a -> b
foldl' :: (b -> a -> b) -> b -> t a -> b
foldr1 :: (a -> a -> a) -> t a -> a
foldl1 :: (a -> a -> a) -> t a -> a
toList :: t a -> [a]
null :: t a -> Bool
length :: t a -> Int
elem :: Eq a => a -> t a -> Bool
maximum :: Ord a => t a -> a
minimum :: Ord a => t a -> a
sum :: Num a => t a -> a
product :: Num a => t a -> a
This may look complicated, but in fact, to make a Foldable instance
you only need to implement one method: your choice of foldMap or
foldr. All the other methods have default implementations in terms
of these, and are included in the class in case more
efficient implementations can be provided.
Instances and examples
The type of foldMap should make it clear what it is supposed to do:
given a way to convert the data in a container into a Monoid (a
function a -> m) and a container of a’s (t a), foldMap
provides a way to iterate over the entire contents of the container,
converting all the a’s to m’s and combining all the m’s with
mappend. The following code shows two examples: a simple
implementation of foldMap for lists, and a binary tree example
provided by the Foldable documentation.
instance Foldable [] where
foldMap :: Monoid m => (a -> m) -> [a] -> m
foldMap g = mconcat . map g
data Tree a = Empty | Leaf a | Node (Tree a) a (Tree a)
instance Foldable Tree where
foldMap :: Monoid m => (a -> m) -> Tree a -> m
foldMap f Empty = mempty
foldMap f (Leaf x) = f x
foldMap f (Node l k r) = foldMap f l `mappend` f k `mappend` foldMap f r
The Foldable module also provides instances for Maybe and Array;
additionally, many of the data structures found in the standard containers library (for example, Map, Set, Tree,
and Sequence) provide their own Foldable instances.
| Exercises |
|---|
|
Derived folds
Given an instance of Foldable, we can write generic,
container-agnostic functions such as:
-- Compute the size of any container.
containerSize :: Foldable f => f a -> Int
containerSize = getSum . foldMap (const (Sum 1))
-- Compute a list of elements of a container satisfying a predicate.
filterF :: Foldable f => (a -> Bool) -> f a -> [a]
filterF p = foldMap (\a -> if p a then [a] else [])
-- Get a list of all the Strings in a container which include the
-- letter a.
aStrings :: Foldable f => f String -> [String]
aStrings = filterF (elem 'a')
The Foldable module also provides a large number of predefined
folds. These used to be generalized versions of Prelude functions of the
same name that only worked on lists; but as of GHC 7.10, the generalized versions themselves are now exported from the Prelude: for example, concat, concatMap, and,
or, any, all, sum, product, maximum(By),
minimum(By), elem, notElem, and find. For example, before GHC 7.10, length used to have type length :: [a] -> Int; now it has type Foldable t => t a -> Int (and is in fact the same as the containerSize function shown above).
The important function toList is also provided, which turns any Foldable structure into a list of its elements in left-right order; it works by folding with the list monoid.
There are also generic functions that work with Applicative or
Monad instances to generate some sort of computation from each
element in a container, and then perform all the side effects from
those computations, discarding the results: traverse_, sequenceA_,
and others. The results must be discarded because the Foldable
class is too weak to specify what to do with them: we cannot, in
general, make an arbitrary Applicative or Monad instance into a Monoid, but we can make m () into a Monoid for any such m. If we do have an Applicative or Monad with a monoid
structure—that is, an Alternative or a MonadPlus—then we can
use the asum or msum functions, which can combine the results as
well. Consult the Foldable documentation for
more details on any of these functions.
Note that the Foldable operations always forget the structure of
the container being folded. If we start with a container of type t a for some Foldable t, then t will never appear in the output
type of any operations defined in the Foldable module. Many times
this is exactly what we want, but sometimes we would like to be able
to generically traverse a container while preserving its
structure—and this is exactly what the Traversable class provides,
which will be discussed in the next section.
| Exercises |
|---|
|
Utility functions
asum :: (Alternative f, Foldable t) => t (f a) -> f atakes a container full of computations and combines them using(<|>).
sequenceA_ :: (Applicative f, Foldable t) => t (f a) -> f ()takes a container full of computations and runs them in sequence, discarding the results (that is, they are used only for their effects). Since the results are discarded, the container only needs to beFoldable. (Compare withsequenceA :: (Applicative f, Traversable t) => t (f a) -> f (t a), which requires a strongerTraversableconstraint in order to be able to reconstruct a container of results having the same shape as the original container.)
traverse_ :: (Applicative f, Foldable t) => (a -> f b) -> t a -> f ()applies the given function to each element in a foldable container and sequences the effects (but discards the results).
for_is the same astraverse_but with its arguments flipped. This is the moral equivalent of a "foreach" loop in an imperative language.
- For historical reasons, there are also variants of all the above with overly-restrictive
Monad(-like) constraints:msumis the same asasumspecialized toMonadPlus, andsequence_,mapM_, andforM_respectively areMonadspecializations ofsequenceA_,traverse_, andfor_.
| Exercises |
|---|
|
Foldable actually isn't
The generic term "fold" is often used to refer to the more technical concept of catamorphism. Intuitively, given a way to summarize "one level of structure" (where recursive subterms have already been replaced with their summaries), a catamorphism can summarize an entire recursive structure. It is important to realize that Foldable does not correspond to catamorphisms, but to something weaker. In particular, Foldable allows observing only the left-right traversal order of elements within a structure, not the actual structure itself. Put another way, every use of Foldable can be expressed in terms of toList. For example, fold itself is equivalent to mconcat . toList.
This is sufficient for many tasks, but not all. For example, consider trying to compute the depth of a Tree: try as we might, there is no way to implement it using Foldable. However, it can be implemented as a catamorphism.
Further reading
The Foldable class had its genesis in McBride and Paterson’s paper
introducing Applicative, although it has
been fleshed out quite a bit from the form in the paper.
An interesting use of Foldable (as well as Traversable) can be
found in Janis Voigtländer’s paper Bidirectionalization for free!.
For more on the relationship between fold, foldMap, and foldr, see foldr is made of monoids.
There was quite a bit of controversy in the Haskell community about a proposal to integrate Foldable (and Traversable) more tightly into the Prelude, known as the FTP. Some of the controversy centered around Foldable instances such as the one for ((,) a), which, together with generalized types for functions such as length :: Foldable t => t a -> Int, allow one to derive seemingly nonsensical results such as length (2,3) = 1. Here is a humorous talk poking fun at the situation.
Traversable
Definition
The Traversable type class, defined in the Data.Traversable
module (haddock), is:
class (Functor t, Foldable t) => Traversable t where
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
sequenceA :: Applicative f => t (f a) -> f (t a)
mapM :: Monad m => (a -> m b) -> t a -> m (t b)
sequence :: Monad m => t (m a) -> m (t a)
As you can see, every Traversable is also a Foldable Functor. To make a Traversable instance, it suffices to implement either traverse or
sequenceA; the other methods all have default implementations in
terms of these. Note that mapM and sequence only exist for historical reasons; especially now that Applicative is a superclass of Monad, they are nothing more than copies of traverse and sequenceA, respectively, but with more restrictive types.
Intuition
The key method of the Traversable class is traverse, which has the following type:
traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
This leads us to view Traversable as a generalization of Functor. traverse is an "effectful fmap": it allows us to map over a structure of type t a, applying a function to every element of type a in order to produce a new structure of type t b; but along the way the function may have some effects (captured by the applicative functor f).
Alternatively, we may consider the sequenceA function. Consider its type:
sequenceA :: Applicative f => t (f a) -> f (t a)
This answers the fundamental question: when can we commute two functors? For example, can we turn a tree of lists into a list of trees?
The ability to compose two monads depends crucially on this ability to
commute functors. Intuitively, if we want to build a composed monad
M a = m (n a) out of monads m and n, then to be able to
implement join :: M (M a) -> M a, that is,
join :: m (n (m (n a))) -> m (n a), we have to be able to commute
the n past the m to get m (m (n (n a))), and then we can use the
joins for m and n to produce something of type m (n a). See
Mark Jones’ paper for more details.
It turns out that given a Functor constraint on the type t, traverse and sequenceA are equivalent in power: either can be implemented in terms of the other.
| Exercises |
|---|
|
Instances and examples
What’s an example of a Traversable instance?
The following code shows an example instance for the same
Tree type used as an example in the previous Foldable section. It
is instructive to compare this instance with a Functor instance for
Tree, which is also shown.
data Tree a = Empty | Leaf a | Node (Tree a) a (Tree a)
instance Traversable Tree where
traverse :: Applicative f => (a -> f b) -> Tree a -> f (Tree b)
traverse g Empty = pure Empty
traverse g (Leaf x) = Leaf <$> g x
traverse g (Node l x r) = Node <$> traverse g l
<*> g x
<*> traverse g r
instance Functor Tree where
fmap :: (a -> b) -> Tree a -> Tree b
fmap g Empty = Empty
fmap g (Leaf x) = Leaf $ g x
fmap g (Node l x r) = Node (fmap g l)
(g x)
(fmap g r)
It should be clear that the Traversable and Functor instances for
Tree are structurally identical; the only difference is that the Functor
instance involves normal function application, whereas the
applications in the Traversable instance take place within an
Applicative context, using (<$>) and (<*>). This same pattern will hold for any type.
Any Traversable functor is also Foldable, and a Functor. We can see
this not only from the class declaration, but by the fact that we can
implement the methods of both classes given only the Traversable
methods.
The standard libraries provide a number of Traversable instances,
including instances for [], ZipList, Maybe, ((,) e), Sum, Product, Either e, Map, Tree, and Sequence.
Notably, Set is not Traversable, although it is Foldable.
| Exercises |
|---|
|
Laws
Any instance of Traversable must satisfy the following two laws, where Identity is the identity functor (as defined in the Data.Functor.Identity module from the transformers package), and Compose wraps the composition of two functors (as defined in Data.Functor.Compose):
traverse Identity = Identitytraverse (Compose . fmap g . f) = Compose . fmap (traverse g) . traverse f
The first law essentially says that traversals cannot make up arbitrary effects. The second law explains how doing two traversals in sequence can be collapsed to a single traversal.
Additionally, suppose eta is an "Applicative morphism", that is,
eta :: forall a f g. (Applicative f, Applicative g) => f a -> g a
and eta preserves the Applicative operations: eta (pure x) = pure x and eta (x <*> y) = eta x <*> eta y. Then, by parametricity, any instance of Traversable satisfying the above two laws will also satisfy eta . traverse f = traverse (eta . f).
Further reading
The Traversable class also had its genesis in McBride and Paterson’s Applicative paper,
and is described in more detail in Gibbons and Oliveira, The Essence of the Iterator Pattern,
which also contains a wealth of references to related work.
Traversable forms a core component of Edward Kmett's lens library. Watching Edward's talk on the subject is a highly recommended way to gain better insight into Traversable, Foldable, Applicative, and many other things besides.
For references on the Traversable laws, see Russell O'Connor's mailing list post (and subsequent thread), and this paper by Jaskelioff and Rypacek for a more in-depth discussion. Daniel Mlot also has this very nice blog post explaining how Traversable arises by considering a variant on the usual Kleisli category of a monad, which also sheds light on where the Traversable laws come from.
This blog post by Will Fancher shows how to use Traversable along with a clever choice of Applicative to efficiently sort any Traversable container.
Bifunctor
Recall that a Functor is a type of kind * -> * where one can "map" a function over the type parameter. (Either e) is a Functor (with fmap :: (a -> b) -> Either e a -> Either e b), as is ((,) e). But there is something oddly asymmetric about these two examples: in principle, there is no reason we can't map over the e instead of the a, for example, like so: lmap :: (e -> e') -> Either e a -> Either e' a. This observation leads directly to the definition of Bifunctor, a class for types of kind * -> * -> * where one can functorially map over both type parameters.
Definition
Here is the type class declaration for Bifunctor, defined
in Data.Bifunctor (since base-4.8, which came with GHC 7.10):
class Bifunctor p where
bimap :: (a -> b) -> (c -> d) -> p a c -> p b d
first :: (a -> b) -> p a c -> p b c
second :: (b -> c) -> p a b -> p a c
We can infer from the fact that p is applied to two type
arguments that its kind must be * -> * -> *. The most
fundamental method of the Bifunctor class is
bimap, which allows mapping over both type arguments at
once. For example,
bimap (+1) length (4, [1,2,3]) = (5,3)
first and second are also provided for
mapping over only one type argument at a time. One is required to
define either bimap, or both first and
second, since default definitions are provided for each
in terms of the others, namely:
bimap f g = first f . second g
first f = bimap f id
second g = bimap id g
Laws
The laws for Bifunctor are entirely analogous to the laws
for Functor. First, mapping with the identity function
should have no effect:
bimap id id = id
first id = id
second id = id
Second, mapping with a composition should be the same as a composition of maps:
bimap (f . g) (h . i) = bimap f h . bimap g i
first (f . g) = first f . first g
second (f . g) = second f . second g
These composition laws actually come "for free" (that is, by
parametricity) once the identity laws are satisfied. One can also
check that the default implementations of first and
second will satisfy the requisite laws if and only if
bimap does, and vice versa.
There is one additional law that relates bimap,
first, and second, namely,
bimap f g = first f . second g
However, this law will hold automatically if one defines only
bimap, or only first and
second, using the default implementation for the others.
So you only need to worry about this law if for some reason (e.g.
efficiency) you define all three of the methods by hand.
One might wonder about the symmetric law bimap f g = second g
. first f; it turns out that once bimap f g = first f
. second g is satisfied, the symmetric version also follows from parametricity.
In summary, there are many laws that can be stated, but most of them
follow automatically from default definitions or from parametricity.
For example, if you define only bimap, then the only law
you actually need to check is bimap id id = id; all the
other laws come for free. Likewise, if you define only
first and second, you only need to check
that first id = id and second id = id.
Instances
(,)andEitherare instances in the evident way.
- Some larger tuple constructors are also instances; for example, the instance for
(,,)maps over the last two components, leaving the first alone. Why anyone would ever want to use this is unclear.
- A value of type
Const a b(to be discussed more in a later section) consists simply of a value of typea;bimap f gmapsfover theaand ignoresg.
Category
Category is a relatively recent addition to the Haskell standard libraries. It generalizes the notion of function composition to general “morphisms”.
∗ GHC 7.6.1 changed its rules regarding types and type variables. Now, any operator at the type level is treated as a type constructor rather than a type variable; prior to GHC 7.6.1 it was possible to use (~>) instead of `arr`. For more information, see the discussion on the GHC-users mailing list. For a new approach to nice arrow notation that works with GHC 7.6.1, see this message and also this message from Edward Kmett, though for simplicity I haven't adopted it here.
The definition of the Category type class (from
Control.Category; haddock) is shown below. For ease of reading, note that I have used an infix type variable `arr`, in parallel with the infix function type constructor (->). ∗ This syntax is not part of Haskell 2010. The second definition shown is the one used in the standard libraries. For the remainder of this document, I will use the infix type constructor `arr` for Category as well as Arrow.
class Category arr where
id :: a `arr` a
(.) :: (b `arr` c) -> (a `arr` b) -> (a `arr` c)
-- The same thing, with a normal (prefix) type constructor
class Category cat where
id :: cat a a
(.) :: cat b c -> cat a b -> cat a c
Note that an instance of Category should be a type which takes two type arguments, that is, something of kind * -> * -> *. It is instructive to imagine the type variable cat replaced by the function constructor (->): indeed, in this case we recover precisely the familiar identity function id and function composition operator (.) defined in the standard Prelude.
Of course, the Category module provides exactly such an instance of
Category for (->). But it also provides one other instance, shown below, which should be familiar from the previous discussion of the Monad laws. Kleisli m a b, as defined in the Control.Arrow module, is just a newtype wrapper around a -> m b.
newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }
instance Monad m => Category (Kleisli m) where
id :: Kleisli m a a
id = Kleisli return
(.) :: Kleisli m b c -> Kleisli m a b -> Kleisli m a c
Kleisli g . Kleisli h = Kleisli (h >=> g)
The only laws that Category instances should satisfy are that id should be the identity of (.), and (.) should be associative. This is kind of like being a monoid, except that, unlike with monoids, not any two values can be composed with (.)---their types have to match up.
Finally, the Category module exports two additional operators:
(<<<), which is just a synonym for (.), and (>>>), which is (.) with its arguments reversed. (In previous versions of the libraries, these operators were defined as part of the Arrow class.)
Further reading
The name Category is a bit misleading, since the Category class cannot represent arbitrary categories, but only categories whose objects are objects of Hask, the category of Haskell types. For a more general treatment of categories within Haskell, see the category-extras package. For more about category theory in general, see the excellent Haskell wikibook page,
Steve Awodey’s new book, Benjamin Pierce’s Basic category theory for computer scientists, or Barr and Wells category theory lecture notes. Benjamin Russell’s blog post
is another good source of motivation and category theory links. You certainly don’t need to know any category theory to be a successful and productive Haskell programmer, but it does lend itself to much deeper appreciation of Haskell’s underlying theory.
Arrow
The Arrow class represents another abstraction of computation, in a
similar vein to Monad and Applicative. However, unlike Monad
and Applicative, whose types only reflect their output, the type of
an Arrow computation reflects both its input and output. Arrows
generalize functions: if arr is an instance of Arrow, a value of
type b `arr` c can be thought of as a computation which takes values of
type b as input, and produces values of type c as output. In the
(->) instance of Arrow this is just a pure function; in general, however,
an arrow may represent some sort of “effectful” computation.
Definition
The definition of the Arrow type class, from
Control.Arrow (haddock), is:
class Category arr => Arrow arr where
arr :: (b -> c) -> (b `arr` c)
first :: (b `arr` c) -> ((b, d) `arr` (c, d))
second :: (b `arr` c) -> ((d, b) `arr` (d, c))
(***) :: (b `arr` c) -> (b' `arr` c') -> ((b, b') `arr` (c, c'))
(&&&) :: (b `arr` c) -> (b `arr` c') -> (b `arr` (c, c'))
∗ In versions of the base
package prior to version 4, there is no Category class, and the
Arrow class includes the arrow composition operator (>>>). It
also includes pure as a synonym for arr, but this was removed
since it conflicts with the pure from Applicative.
The first thing to note is the Category class constraint, which
means that we get identity arrows and arrow composition for free:
given two arrows g :: b `arr` c and h :: c `arr` d, we can form their
composition g >>> h :: b `arr` d ∗.
As should be a familiar pattern by now, the only methods which must be
defined when writing a new instance of Arrow are arr and first;
the other methods have default definitions in terms of these, but are
included in the Arrow class so that they can be overridden with more
efficient implementations if desired.
Note that first and second conflict with methods of the same name from Data.Bifunctor. If you want to use both for some reason, you will need to import one or both qualified. It used to be common to import Control.Arrow just to get the (->) instance for use in editing pairs using first or second; now it is recommended to import Data.Bifunctor for this purpose instead. (Notice that for the (->) instance of Arrow and the (,) instance of Bifunctor, first and second specialize to the same type.)
Intuition
Let’s look at each of the arrow methods in turn. Ross Paterson’s web page on arrows has nice diagrams which can help build intuition.
- The
arrfunction takes any functionb -> cand turns it into a generalized arrowb `arr` c. Thearrmethod justifies the claim that arrows generalize functions, since it says that we can treat any function as an arrow. It is intended that the arrowarr gis “pure” in the sense that it only computesgand has no “effects” (whatever that might mean for any particular arrow type).
- The
firstmethod turns any arrow frombtocinto an arrow from(b,d)to(c,d). The idea is thatfirst gusesgto process the first element of a tuple, and lets the second element pass through unchanged. For the function instance ofArrow, of course,first g (x,y) = (g x, y).
- The
secondfunction is similar tofirst, but with the elements of the tuples swapped. Indeed, it can be defined in terms offirstusing an auxiliary functionswap, defined byswap (x,y) = (y,x).
- The
(***)operator is “parallel composition” of arrows: it takes two arrows and makes them into one arrow on tuples, which has the behavior of the first arrow on the first element of a tuple, and the behavior of the second arrow on the second element. The mnemonic is thatg *** his the product (hence*) ofgandh. For the function instance ofArrow, we define(g *** h) (x,y) = (g x, h y). The default implementation of(***)is in terms offirst,second, and sequential arrow composition(>>>). The reader may also wish to think about how to implementfirstandsecondin terms of(***).
- The
(&&&)operator is “fanout composition” of arrows: it takes two arrowsgandhand makes them into a new arrowg &&& hwhich supplies its input as the input to bothgandh, returning their results as a tuple. The mnemonic is thatg &&& hperforms bothgandh(hence&) on its input. For functions, we define(g &&& h) x = (g x, h x).
Instances
The Arrow library itself only provides two Arrow instances, both
of which we have already seen: (->), the normal function
constructor, and Kleisli m, which makes functions of
type a -> m b into Arrows for any Monad m. These instances are:
instance Arrow (->) where
arr :: (b -> c) -> (b -> c)
arr g = g
first :: (b -> c) -> ((b,d) -> (c,d))
first g (x,y) = (g x, y)
newtype Kleisli m a b = Kleisli { runKleisli :: a -> m b }
instance Monad m => Arrow (Kleisli m) where
arr :: (b -> c) -> Kleisli m b c
arr f = Kleisli (return . f)
first :: Kleisli m b c -> Kleisli m (b,d) (c,d)
first (Kleisli f) = Kleisli (\ ~(b,d) -> do c <- f b
return (c,d) )
Laws
∗ See John Hughes: Generalising monads to arrows; Sam Lindley, Philip Wadler, Jeremy Yallop: The arrow calculus; Ross Paterson: Programming with Arrows.
There are quite a few laws that instances of Arrow should
satisfy ∗:
arr id = id
arr (h . g) = arr g >>> arr h
first (arr g) = arr (g *** id)
first (g >>> h) = first g >>> first h
first g >>> arr (id *** h) = arr (id *** h) >>> first g
first g >>> arr fst = arr fst >>> g
first (first g) >>> arr assoc = arr assoc >>> first g
assoc ((x,y),z) = (x,(y,z))
Note that this version of the laws is slightly different than the laws given in the
first two above references, since several of the laws have now been
subsumed by the Category laws (in particular, the requirements that
id is the identity arrow and that (>>>) is associative). The laws
shown here follow those in Paterson’s Programming with Arrows, which uses the
Category class.
∗ Unless category-theory-induced insomnolence is your cup of tea.
The reader is advised not to lose too much sleep over the Arrow
laws ∗, since it is not essential to understand them in order to
program with arrows. There are also laws that ArrowChoice,
ArrowApply, and ArrowLoop instances should satisfy; the interested
reader should consult Paterson: Programming with Arrows.
ArrowChoice
Computations built using the Arrow class, like those built using
the Applicative class, are rather inflexible: the structure of the computation
is fixed at the outset, and there is no ability to choose between
alternate execution paths based on intermediate results.
The ArrowChoice class provides exactly such an ability:
class Arrow arr => ArrowChoice arr where
left :: (b `arr` c) -> (Either b d `arr` Either c d)
right :: (b `arr` c) -> (Either d b `arr` Either d c)
(+++) :: (b `arr` c) -> (b' `arr` c') -> (Either b b' `arr` Either c c')
(|||) :: (b `arr` d) -> (c `arr` d) -> (Either b c `arr` d)
A comparison of ArrowChoice to Arrow will reveal a striking
parallel between left, right, (+++), (|||) and first,
second, (***), (&&&), respectively. Indeed, they are dual:
first, second, (***), and (&&&) all operate on product types
(tuples), and left, right, (+++), and (|||) are the
corresponding operations on sum types. In general, these operations
create arrows whose inputs are tagged with Left or Right, and can
choose how to act based on these tags.
- If
gis an arrow frombtoc, thenleft gis an arrow fromEither b dtoEither c d. On inputs tagged withLeft, theleft garrow has the behavior ofg; on inputs tagged withRight, it behaves as the identity.
- The
rightfunction, of course, is the mirror image ofleft. The arrowright ghas the behavior ofgon inputs tagged withRight.
- The
(+++)operator performs “multiplexing”:g +++ hbehaves asgon inputs tagged withLeft, and ashon inputs tagged withRight. The tags are preserved. The(+++)operator is the sum (hence+) of two arrows, just as(***)is the product.
- The
(|||)operator is “merge” or “fanin”: the arrowg ||| hbehaves asgon inputs tagged withLeft, andhon inputs tagged withRight, but the tags are discarded (hence,gandhmust have the same output type). The mnemonic is thatg ||| hperforms eithergorhon its input.
The ArrowChoice class allows computations to choose among a finite number of execution paths, based on intermediate results. The possible
execution paths must be known in advance, and explicitly assembled with (+++) or (|||). However, sometimes more flexibility is
needed: we would like to be able to compute an arrow from intermediate results, and use this computed arrow to continue the computation. This is the power given to us by ArrowApply.
ArrowApply
The ArrowApply type class is:
class Arrow arr => ArrowApply arr where
app :: (b `arr` c, b) `arr` c
If we have computed an arrow as the output of some previous
computation, then app allows us to apply that arrow to an input,
producing its output as the output of app. As an exercise, the
reader may wish to use app to implement an alternative “curried”
version, app2 :: b `arr` ((b `arr` c) `arr` c).
This notion of being able to compute a new computation
may sound familiar:
this is exactly what the monadic bind operator (>>=) does. It
should not particularly come as a surprise that ArrowApply and
Monad are exactly equivalent in expressive power. In particular,
Kleisli m can be made an instance of ArrowApply, and any instance
of ArrowApply can be made a Monad (via the newtype wrapper
ArrowMonad). As an exercise, the reader may wish to try
implementing these instances:
class Arrow arr => ArrowApply arr where
app :: (b `arr` c, b) `arr` c
instance Monad m => ArrowApply (Kleisli m) where
app :: Kleisli m (Kleisli m b c, b) c
app = -- exercise
newtype ArrowApply a => ArrowMonad a b = ArrowMonad (a () b)
instance ArrowApply a => Monad (ArrowMonad a) where
return :: b -> ArrowMonad a b
return = -- exercise
(>>=) :: ArrowMonad a a -> (a -> ArrowMonad a b) -> ArrowMonad a b
(ArrowMonad a) >>= k = -- exercise
ArrowLoop
The ArrowLoop type class is:
class Arrow a => ArrowLoop a where
loop :: a (b, d) (c, d) -> a b c
trace :: ((b,d) -> (c,d)) -> b -> c
trace f b = let (c,d) = f (b,d) in c
It describes arrows that can use recursion to compute results, and is
used to desugar the rec construct in arrow notation (described
below).
Taken by itself, the type of the loop method does not seem to tell
us much. Its intention, however, is a generalization of the trace
function which is also shown. The d component of the first arrow’s
output is fed back in as its own input. In other words, the arrow
loop g is obtained by recursively “fixing” the second component of
the input to g.
It can be a bit difficult to grok what the trace function is doing.
How can d appear on the left and right sides of the let? Well,
this is Haskell’s laziness at work. There is not space here for a
full explanation; the interested reader is encouraged to study the
standard fix function, and to read Paterson’s arrow tutorial.
Arrow notation
Programming directly with the arrow combinators can be painful,
especially when writing complex computations which need to retain
simultaneous reference to a number of intermediate results. With
nothing but the arrow combinators, such intermediate results must be
kept in nested tuples, and it is up to the programmer to remember
which intermediate results are in which components, and to swap,
reassociate, and generally mangle tuples as necessary. This problem
is solved by the special arrow notation supported by GHC, similar to
do notation for monads, that allows names to be assigned to
intermediate results while building up arrow computations. An example
arrow implemented using arrow notation, taken from
Paterson, is:
class ArrowLoop arr => ArrowCircuit arr where
delay :: b -> (b `arr` b)
counter :: ArrowCircuit arr => Bool `arr` Int
counter = proc reset -> do
rec output <- idA -< if reset then 0 else next
next <- delay 0 -< output + 1
idA -< output
This arrow is intended to represent a recursively defined counter circuit with a reset line.
There is not space here for a full explanation of arrow notation; the interested reader should consult Paterson’s paper introducing the notation, or his later tutorial which presents a simplified version.
Further reading
An excellent starting place for the student of arrows is the arrows web page, which contains an introduction and many references. Some key papers on arrows include Hughes’ original paper introducing arrows, Generalising monads to arrows, and Paterson’s paper on arrow notation.
Both Hughes and Paterson later wrote accessible tutorials intended for a broader audience: Paterson: Programming with Arrows and Hughes: Programming with Arrows.
Although Hughes’ goal in defining the Arrow class was to
generalize Monads, and it has been said that Arrow lies “between
Applicative and Monad” in power, they are not directly
comparable. The precise relationship remained in some confusion until
analyzed by Lindley, Wadler, and Yallop, who
also invented a new calculus of arrows, based on the lambda calculus,
which considerably simplifies the presentation of the arrow laws
(see The arrow calculus). There is also a precise technical sense in which Arrow can be seen as the intersection of Applicative and Category.
Some examples of Arrows include Yampa, the
Haskell XML Toolkit, and the functional GUI library Grapefruit.
Some extensions to arrows have been explored; for example, the
BiArrows of Alimarine et al. ("There and Back Again: Arrows for Invertible Programming"), for two-way instead of one-way
computation.
The Haskell wiki has links to many additional research papers relating to Arrows.
Comonad
The final type class we will examine is Comonad. The Comonad class
is the categorical dual of Monad; that is, Comonad is like Monad
but with all the function arrows flipped. It is not actually in the
standard Haskell libraries, but it has seen some interesting uses
recently, so we include it here for completeness.
Definition
The Comonad type class, defined in the Control.Comonad module of
the comonad library, is:
class Functor w => Comonad w where
extract :: w a -> a
duplicate :: w a -> w (w a)
duplicate = extend id
extend :: (w a -> b) -> w a -> w b
extend f = fmap f . duplicate
As you can see, extract is the dual of return, duplicate is the dual of join, and extend is the dual of (=<<). The definition of Comonad is a bit redundant, giving the programmer the choice on whether extend or duplicate are implemented; the other operation then has a default implementation.
A prototypical example of a Comonad instance is:
-- Infinite lazy streams
data Stream a = Cons a (Stream a)
-- 'duplicate' is like the list function 'tails'
-- 'extend' computes a new Stream from an old, where the element
-- at position n is computed as a function of everything from
-- position n onwards in the old Stream
instance Comonad Stream where
extract :: Stream a -> a
extract (Cons x _) = x
duplicate :: Stream a -> Stream (Stream a)
duplicate s@(Cons x xs) = Cons s (duplicate xs)
extend :: (Stream a -> b) -> Stream a -> Stream b
extend g s@(Cons x xs) = Cons (g s) (extend g xs)
-- = fmap g (duplicate s)
Further reading
Dan Piponi explains in a blog post what cellular automata have to do with comonads. In another blog post, Conal Elliott has examined a comonadic formulation of functional reactive programming. Sterling Clover’s blog post Comonads in everyday life explains the relationship between comonads and zippers, and how comonads can be used to design a menu system for a web site.
Uustalu and Vene have a number of papers exploring ideas related to comonads and functional programming:
- Comonadic Notions of Computation
- The dual of substitution is redecoration (Also available as ps.gz.)
- Recursive coalgebras from comonads
- Recursion schemes from comonads
- The Essence of Dataflow Programming.
Gabriel Gonzalez's Comonads are objects points out similarities between comonads and object-oriented programming.
The comonad-transformers package contains comonad transformers.
Acknowledgements
A special thanks to all of those who taught me about standard Haskell type classes and helped me develop good intuition for them, particularly Jules Bean (quicksilver), Derek Elkins (ddarius), Conal Elliott (conal), Cale Gibbard (Cale), David House, Dan Piponi (sigfpe), and Kevin Reid (kpreid).
I also thank the many people who provided a mountain of helpful feedback and suggestions on a first draft of the Typeclassopedia: David Amos, Kevin Ballard, Reid Barton, Doug Beardsley, Joachim Breitner, Andrew Cave, David Christiansen, Gregory Collins, Mark Jason Dominus, Conal Elliott, Yitz Gale, George Giorgidze, Steven Grady, Travis Hartwell, Steve Hicks, Philip Hölzenspies, Edward Kmett, Eric Kow, Serge Le Huitouze, Felipe Lessa, Stefan Ljungstrand, Eric Macaulay, Rob MacAulay, Simon Meier, Eric Mertens, Tim Newsham, Russell O’Connor, Conrad Parker, Walt Rorie-Baety, Colin Ross, Tom Schrijvers, Aditya Siram, C. Smith, Martijn van Steenbergen, Joe Thornber, Jared Updike, Rob Vollmert, Andrew Wagner, Louis Wasserman, and Ashley Yakeley, as well as a few only known to me by their IRC nicks: b_jonas, maltem, tehgeekmeister, and ziman. I have undoubtedly omitted a few inadvertently, which in no way diminishes my gratitude.
Finally, I would like to thank Wouter Swierstra for his fantastic work editing the Monad.Reader, and my wife Joyia for her patience during the process of writing the Typeclassopedia.
About the author
Brent Yorgey (blog, homepage) is (as of November 2011) a fourth-year Ph.D. student in the programming languages group at the University of Pennsylvania. He enjoys teaching, creating EDSLs, playing Bach fugues, musing upon category theory, and cooking tasty lambda-treats for the denizens of #haskell.
Colophon
The Typeclassopedia was written by Brent Yorgey and initially published in March 2009. Painstakingly converted to wiki syntax by User:Geheimdienst in November 2011, after asking Brent’s permission.
If something like this TeX to wiki syntax conversion ever needs to be done again, here are some vim commands that helped:
- %s/\\section{\([^}]*\)}/=\1=/gc
- %s/\\subsection{\([^}]*\)}/==\1==/gc
- %s/^ *\\item /\r* /gc
- %s/---/—/gc
- %s/\$\([^$]*\)\$/<math>\1\\ <\/math>/gc Appending “\ ” forces images to be rendered. Otherwise, Mediawiki would go back and forth between one font for short <math> tags, and another more TeX-like font for longer tags (containing more than a few characters)""
- %s/|\([^|]*\)|/<code>\1<\/code>/gc
- %s/\\dots/.../gc
- %s/^\\label{.*$//gc
- %s/\\emph{\([^}]*\)}/''\1''/gc
- %s/\\term{\([^}]*\)}/''\1''/gc
The biggest issue was taking the academic-paper-style citations and turning them into hyperlinks with an appropriate title and an appropriate target. In most cases there was an obvious thing to do (e.g. online PDFs of the cited papers or CiteSeer entries). Sometimes, however, it’s less clear and you might want to check the original Typeclassopedia PDF with the original bibliography file.
To get all the citations into the main text, I first tried processing the source with TeX or Lyx. This didn’t work due to missing unfindable packages, syntax errors, and my general ineptitude with TeX.
I then went for the next best solution, which seemed to be extracting all instances of “\cite{something}” from the source and in that order pulling the referenced entries from the .bib file. This way you can go through the source file and sorted-references file in parallel, copying over what you need, without searching back and forth in the .bib file. I used:
- egrep -o "\cite\{[^\}]*\}" ~/typeclassopedia.lhs | cut -c 6- | tr "," "\n" | tr -d "}" > /tmp/citations
- for i in $(cat /tmp/citations); do grep -A99 "$i" ~/typeclassopedia.bib|egrep -B99 '^\}$' -m1 ; done > ~/typeclasso-refs-sorted