Zipper monad
The TravelTree Monad is a monad proposed and designed by Paolo Martini (xerox), and coded by David House (davidhouse). It is based on the State monad and is used for navigating around in binary trees, using the concept of TheZipper.
Definition
newtype Travel t a = Travel { unT :: State t a }
deriving (Functor, Monad, MonadState t)
type TravelTree a = Travel (Loc a) (Tree a)
Computations in TravelTree are stateful. Loc a and Tree a are defined as follows:
data Tree a = Leaf a | Branch (Tree a) (Tree a)
data Cxt a = Top
| L (Cxt a) (Tree a)
| R (Tree a) (Cxt a)
deriving (Show)
type Loc a = (Tree a, Cxt a)
See TheZipper for an explanation of the Cxt and Loc concepts.
Functions
Moving around
There are four main functions for stringing together TravelTree computations:
left, -- moves down a level, through the left branch
right, -- moves down a level, through the right branch
up, -- moves to the node's parent
top -- moves to the top node
:: TravelTree a
All four return the subtree at the new location.
Mutation
There are also functions available for changing the tree:
getTree :: TravelTree a
putTree :: Tree a -> TravelTree a
modifyTree :: (Tree a -> Tree a) -> TravelTree a
These are direct front-doors for State's get, put and modify, and all three return the subtree after any applicable modifications.
Exit points
To get out of the monad, use traverse:
traverse :: Tree a -> TravelTree a -> Tree a
Again, this is just a front-door for evalState, with an initial state of (tt, Top) where tt is the TravelTree passed in.
Examples
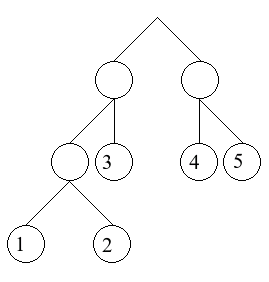
The following examples use as the example tree:
t = Branch (Branch (Branch (Leaf 1) (Leaf 2))
(Leaf 3))
(Branch (Leaf 4)
(Leaf 5))
Code
data Cxt a = Top
| L (Cxt a) (Tree a)
| R (Tree a) (Cxt a)
deriving (Show)
type Loc a = (Tree a, Cxt a)
newtype Travel t a = Travel { unT :: State t a }
deriving (Functor, Monad, MonadState t)
type TravelTree a = Travel (Loc a) (Tree a)
t = Branch (Branch (Branch (Leaf 1) (Leaf 2))
(Leaf 3))
(Branch (Leaf 4)
(Leaf 5))
left :: TravelTree a
left = modify left' >> liftM fst get where
left' (Branch l r, c) = (l, L c r)
right :: TravelTree a
right = modify right' >> liftM fst get where
right' (Branch l r, c) = (r, R l c)
up :: TravelTree a
up = modify up' >> liftM fst get where
up' (t, L c r) = (Branch t r, c)
up' (t, R l c) = (Branch l t, c)
top :: TravelTree a
top = modify (second $ const Top) >> liftM fst get
modifyTree :: (Tree a -> Tree a) -> TravelTree a
modifyTree f = modify (first f) >> liftM fst get
putTree :: Tree a -> TravelTree a
putTree t = modifyTree $ const t
getTree :: TravelTree a
getTree = modifyTree id -- works because modifyTree returns the 'new' tree
traverse :: Tree a -> TravelTree a -> Tree a
traverse t tt = evalState (unT tt) (t, Top)
leftLeftRight :: TravelTree a
leftLeftRight = do left
left
right
revTreeZipper :: Tree a -> Tree a
revTreeZipper t = t `traverse` revTreeZipper' where
revTreeZipper' :: TravelTree a
revTreeZipper' = do t <- getTree
case t of
Branch _ _ -> do left
l' <- revTreeZipper'
up
right
r' <- revTreeZipper'
up
putTree $ Branch r' l'
Leaf x -> return $ Leaf x