99 questions/Solutions/70
(**) Tree construction from a node string.
We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level.
By this rule, the tree below (tree5) is represented as: afg^^c^bd^e^^^
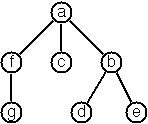
Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. Make your predicate work in both directions.
We could write separate printing and parsing functions, but the problem statement asks for a bidirectional function.
First we need a parser monad, with some primitives:
newtype P a = P { runP :: String -> Maybe (a, String) }
instance Monad P where
return x = P $ \ s -> Just (x, s)
P v >>= f = P $ \ s -> do
(x, s') <- v s
runP (f x) s'
instance MonadPlus P where
mzero = P $ \ _ -> Nothing
P u `mplus` P v = P $ \ s -> u s `mplus` v s
charP :: P Char
charP = P view_list
where view_list [] = Nothing
view_list (c:cs) = Just (c, cs)
literalP :: Char -> P ()
literalP c = do { c' <- charP; guard (c == c') }
spaceP :: P ()
spaceP = P (\ s -> Just ((), dropWhile isSpace s))
Next a Syntax type, combining printing and parsing functions:
data Syntax a = Syntax {
display :: a -> String,
parse :: P a
}
(We don't use a class, because we want multiple syntaxes for a given type.) Some combinators for building syntaxes:
-- concatenation
(<*>) :: Syntax a -> Syntax b -> Syntax (a,b)
a <*> b = Syntax {
display = \ (va,vb) -> display a va ++ display b vb,
parse = liftM2 (,) (parse a) (parse b)
}
-- alternatives
(<|>) :: Syntax a -> Syntax b -> Syntax (Either a b)
a <|> b = Syntax {
display = either (display a) (display b),
parse = liftM Left (parse a) `mplus` liftM Right (parse b)
}
char :: Syntax Char
char = Syntax return charP
literal :: Char -> Syntax ()
literal c = Syntax (const [c]) (literalP c)
space :: Syntax ()
space = Syntax (const " ") spaceP
iso :: (a -> b) -> (b -> a) -> Syntax a -> Syntax b
iso a_to_b b_to_a a = Syntax {
display = display a . b_to_a,
parse = liftM a_to_b (parse a)
}
The last one maps a syntax using an isomorphism between types. Some uses of this function:
-- concatenation, with no value in the first part
(*>) :: Syntax () -> Syntax a -> Syntax a
p *> q = iso snd ((,) ()) (p <*> q)
-- list of a's, followed by finish
list :: Syntax a -> Syntax () -> Syntax [a]
list a finish = iso toList fromList (finish <|> (a <*> list a finish))
where toList (Left _) = []
toList (Right (x, xs)) = x:xs
fromList [] = Left ()
fromList (x:xs) = Right (x, xs)
Now we can define the syntax of depth-first presentations:
df :: Syntax (Tree Char)
df = iso toTree fromTree (char <*> list df (literal '^'))
where toTree (x, ts) = Node x ts
fromTree (Node x ts) = (x, ts)
We are using the isomorphism between Tree a and (a, [Tree a]). Some examples:
Tree> display df tree5
"afg^^c^bd^e^^^"
Tree> runP (parse df) "afg^^c^bd^e^^^"
Just (Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]],"")
A more naive solution, trying to split the string with stack
stringToTree :: String -> Tree Char
stringToTree (x:xs@(y:ys))
| y == '^' = Node x []
| otherwise = Node x (map stringToTree subs)
where subs = snd $ foldl parse ([],[]) $ init xs
parse ([],[]) z = ([z], [[z]])
parse (stack, acc) z = (stack', acc')
where stack'
| z == '^' = init stack
| otherwise = stack ++ [z]
acc' = if stack == []
then acc ++ [[z]]
else (init acc) ++ [(last acc) ++ [z]]
A simple solution that uses Standard Prelude functions:
stringToTree :: String -> Tree Char
stringToTree (x:'^':"") = Node x []
stringToTree (x:xs) = Node x ys
where
z = map fst $ filter ((==) 0 . snd) $ zip [0..] $
scanl (+) 0 $ map (\x -> if x == '^' then -1 else 1) xs
ys = map (stringToTree . uncurry (sub xs)) $ zip (init z) (tail z)
sub s a b = take (b - a) $ drop a s
A solution similar to that of problem 69, special casing the root node:
stringToTree :: String -> Tree Char
stringToTree (x:xs) = Node x (fst (stringToTrees xs))
where stringToTrees (x:xs)
| x == '^' = ([], xs)
| otherwise = ([Node x trees0] ++ trees1, rest1)
where (trees0, rest0) = stringToTrees xs
(trees1, rest1) = stringToTrees rest0
It's more direct to convert Tree back to string
import Data.List
treeToString :: Tree Char -> String
treeToString (Node x ts)
= [x] ++ (concat $ intersperse "^" (map treeToString ts)) ++ "^"
The exercise was really designed for Prolog, and calls for a bidirectional predicate. The closest thing to that, in Haskell, is a class! This is really a parsing/pretty-printing solution, with the names to match. Rather than trying to work with strings and a special "up" character (which won't really work at the type level), we use lists of explicit instructions. The requested predicate is BuildTree.
{-# language MultiParamTypeClasses, FunctionalDependencies,
FlexibleContexts, FlexibleInstances, UndecidableInstances,
DataKinds, PolyKinds #-}
import Data.Tree
data Instr c = Up | Down c
class ParseTree str t '[]
=> BuildTree (str :: [Instr c]) (t :: Tree c) | str -> t, t -> str
instance ParseTree str t '[]
=> BuildTree str t
We use two helpers to implement it:
class ParseTree (str :: [Instr c]) (t :: Tree c) (rem :: [Instr c])
| str -> t rem, t rem -> str
class ParseForest (str :: [Instr c]) (ts :: [Tree c]) (rem :: [Instr c])
| str -> ts rem, ts rem -> str
instance ParseTree ('Down c ': 'Up ': r) ('Node c '[]) r
instance ParseForest ('Down d ': is) (t ': ts) r
=> ParseTree ('Down c ': 'Down d ': is) ('Node c (t ': ts)) r
instance ParseForest ('Up ': is) '[] is
instance ( ParseTree ('Down c ': is) t r
, ParseForest r ts r')
=> ParseForest ('Down c ': is) (t ': ts) r'