Difference between revisions of "99 questions/61 to 69"
m |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
This is part of [[H-99:_Ninety-Nine_Haskell_Problems|Ninety-Nine Haskell Problems]], based on [https://prof.ti.bfh.ch/hew1/informatik3/prolog/p-99/ Ninety-Nine Prolog Problems]. |
This is part of [[H-99:_Ninety-Nine_Haskell_Problems|Ninety-Nine Haskell Problems]], based on [https://prof.ti.bfh.ch/hew1/informatik3/prolog/p-99/ Ninety-Nine Prolog Problems]. |
||
| − | = |
+ | <h2 style="border:none">Binary trees</h2> |
| − | As defined |
+ | As defined [[99 questions/54A to 60|here]]. |
An example tree: |
An example tree: |
||
| Line 12: | Line 12: | ||
(Branch 2 Empty Empty) |
(Branch 2 Empty Empty) |
||
</haskell> |
</haskell> |
||
| + | |||
== Problem 61 == |
== Problem 61 == |
||
| + | <div style="border-bottom:1px solid #eee">Count the leaves of a binary tree. <span style="float:right"><small>[[99 questions/Solutions/61|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | Count the leaves of a binary tree |
||
| + | <br> |
||
A leaf is a node with no successors. Write a predicate count_leaves/2 to count them. |
A leaf is a node with no successors. Write a predicate count_leaves/2 to count them. |
||
| Line 28: | Line 30: | ||
<haskell> |
<haskell> |
||
| − | > countLeaves tree4 |
+ | λ> countLeaves tree4 |
2 |
2 |
||
</haskell> |
</haskell> |
||
| − | [[99 questions/Solutions/61 | Solutions]] |
||
== Problem 61A == |
== Problem 61A == |
||
| + | <div style="border-bottom:1px solid #eee">Collect the leaves of a binary tree in a list. <span style="float:right"><small>[[99 questions/Solutions/61A|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | Collect the leaves of a binary tree in a list |
||
| + | <br> |
||
A leaf is a node with no successors. Write a predicate leaves/2 to collect them in a list. |
A leaf is a node with no successors. Write a predicate leaves/2 to collect them in a list. |
||
| Line 49: | Line 51: | ||
<haskell> |
<haskell> |
||
| − | > leaves tree4 |
+ | λ> leaves tree4 |
[4,2] |
[4,2] |
||
</haskell> |
</haskell> |
||
| − | [[99 questions/Solutions/61A | Solutions]] |
||
== Problem 62 == |
== Problem 62 == |
||
| + | <div style="border-bottom:1px solid #eee">Collect the internal nodes of a binary tree in a list. <span style="float:right"><small>[[99 questions/Solutions/62|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | Collect the internal nodes of a binary tree in a list |
||
| + | <br> |
||
An internal node of a binary tree has either one or two non-empty successors. Write a predicate internals/2 to collect them in a list. |
An internal node of a binary tree has either one or two non-empty successors. Write a predicate internals/2 to collect them in a list. |
||
| Line 70: | Line 72: | ||
<haskell> |
<haskell> |
||
| − | + | λ> internals tree4 |
|
| − | + | [1,2] |
|
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/62 | Solutions]] |
||
== Problem 62B == |
== Problem 62B == |
||
| + | <div style="border-bottom:1px solid #eee">Collect the nodes at a given level in a list. <span style="float:right"><small>[[99 questions/Solutions/62B|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | Collect the nodes at a given level in a list |
||
| + | <br> |
||
A node of a binary tree is at level N if the path from the root to the node has length N-1. The root node is at level 1. Write a predicate atlevel/3 to collect all nodes at a given level in a list. |
A node of a binary tree is at level N if the path from the root to the node has length N-1. The root node is at level 1. Write a predicate atlevel/3 to collect all nodes at a given level in a list. |
||
| Line 92: | Line 93: | ||
<haskell> |
<haskell> |
||
| − | + | λ> atLevel tree4 2 |
|
| − | + | [2,2] |
|
</haskell> |
</haskell> |
||
| − | [[99 questions/Solutions/62B | Solutions]] |
||
== Problem 63 == |
== Problem 63 == |
||
| + | <div style="border-bottom:1px solid #eee">Construct a complete binary tree. <span style="float:right"><small>[[99 questions/Solutions/63|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | Construct a complete binary tree |
||
| + | <br> |
||
A complete binary tree with height H is defined as follows: |
A complete binary tree with height H is defined as follows: |
||
| Line 121: | Line 122: | ||
<haskell> |
<haskell> |
||
| + | λ> completeBinaryTree 4 |
||
| − | Main> complete_binary_tree 4 |
||
Branch 'x' (Branch 'x' (Branch 'x' Empty Empty) Empty) (Branch 'x' Empty Empty) |
Branch 'x' (Branch 'x' (Branch 'x' Empty Empty) Empty) (Branch 'x' Empty Empty) |
||
| − | + | λ> isCompleteBinaryTree $ Branch 'x' (Branch 'x' Empty Empty) (Branch 'x' Empty Empty) |
|
True |
True |
||
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/63 | Solutions]] |
||
== Problem 64 == |
== Problem 64 == |
||
| + | <div style="border-bottom:1px solid #eee">Layout algorithm for displaying trees. <span style="float:right"><small>[[99 questions/Solutions/64|Solutions]]</small></span> |
||
| + | </div> |
||
| + | <br> |
||
Given a binary tree as the usual Prolog term t(X,L,R) (or nil). As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration below: |
Given a binary tree as the usual Prolog term t(X,L,R) (or nil). As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration below: |
||
| − | https:// |
+ | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p64.gif |
In this layout strategy, the position of a node v is obtained by the following two rules: |
In this layout strategy, the position of a node v is obtained by the following two rules: |
||
| Line 174: | Line 176: | ||
<haskell> |
<haskell> |
||
| − | > layout tree64 |
+ | λ> layout tree64 |
Branch ('n',(8,1)) (Branch ('k',(6,2)) (Branch ('c',(2,3)) ... |
Branch ('n',(8,1)) (Branch ('k',(6,2)) (Branch ('c',(2,3)) ... |
||
</haskell> |
</haskell> |
||
| − | [[99 questions/Solutions/64 | Solutions]] |
||
| − | |||
== Problem 65 == |
== Problem 65 == |
||
| + | <div style="border-bottom:1px solid #eee">Layout algorithm for displaying trees (part 2). <span style="float:right"><small>[[99 questions/Solutions/65|Solutions]]</small></span> |
||
| + | </div> |
||
| + | <br> |
||
An alternative layout method is depicted in the illustration below: |
An alternative layout method is depicted in the illustration below: |
||
| − | https:// |
+ | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p65.gif |
Find out the rules and write the corresponding function. |
Find out the rules and write the corresponding function. |
||
| Line 218: | Line 221: | ||
<haskell> |
<haskell> |
||
| − | > layout tree65 |
+ | λ> layout tree65 |
Branch ('n',(15,1)) (Branch ('k',(7,2)) (Branch ('c',(3,3)) ... |
Branch ('n',(15,1)) (Branch ('k',(7,2)) (Branch ('c',(3,3)) ... |
||
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/65 | Solutions]] |
||
== Problem 66 == |
== Problem 66 == |
||
| + | <div style="border-bottom:1px solid #eee">Layout algorithm for displaying trees (part 3). <span style="float:right"><small>[[99 questions/Solutions/66|Solutions]]</small></span> |
||
| + | </div> |
||
| + | <br> |
||
Yet another layout strategy is shown in the illustration below: |
Yet another layout strategy is shown in the illustration below: |
||
| − | https:// |
+ | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p66.gif |
The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding Prolog predicate. Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree? |
The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding Prolog predicate. Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree? |
||
| Line 240: | Line 244: | ||
<haskell> |
<haskell> |
||
| − | > layout tree65 |
+ | λ> layout tree65 |
Branch ('n',(5,1)) (Branch ('k',(3,2)) (Branch ('c',(2,3)) ... |
Branch ('n',(5,1)) (Branch ('k',(3,2)) (Branch ('c',(2,3)) ... |
||
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/66 | Solutions]] |
||
== Problem 67A == |
== Problem 67A == |
||
| + | <div style="border-bottom:1px solid #eee">A string representation of binary trees. <span style="float:right"><small>[[99 questions/Solutions/67A|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | A string representation of binary trees |
||
| + | <br> |
||
Somebody represents binary trees as strings of the following type: |
Somebody represents binary trees as strings of the following type: |
||
| Line 269: | Line 272: | ||
<haskell> |
<haskell> |
||
| − | + | λ> stringToTree "x(y,a(,b))" >>= print |
|
Branch 'x' (Branch 'y' Empty Empty) (Branch 'a' Empty (Branch 'b' Empty Empty)) |
Branch 'x' (Branch 'y' Empty Empty) (Branch 'a' Empty (Branch 'b' Empty Empty)) |
||
| − | + | λ> let t = cbtFromList ['a'..'z'] in stringToTree (treeToString t) >>= print . (== t) |
|
True |
True |
||
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/67A | Solutions]] |
||
== Problem 68 == |
== Problem 68 == |
||
| + | <div style="border-bottom:1px solid #eee">Preorder and inorder sequences of binary trees. <span style="float:right"><small>[[99 questions/Solutions/68|Solutions]]</small></span> |
||
| + | </div> |
||
| + | <br> |
||
| − | + | We consider binary trees with nodes that are identified by single lower-case letters, as in the example of Problem 67. |
|
a) Write predicates preorder/2 and inorder/2 that construct the preorder and inorder sequence of a given binary tree, respectively. The results should be atoms, e.g. 'abdecfg' for the preorder sequence of the example in problem P67. |
a) Write predicates preorder/2 and inorder/2 that construct the preorder and inorder sequence of a given binary tree, respectively. The results should be atoms, e.g. 'abdecfg' for the preorder sequence of the example in problem P67. |
||
| Line 291: | Line 295: | ||
<haskell> |
<haskell> |
||
| − | + | λ> let { Just t = stringToTree "a(b(d,e),c(,f(g,)))" ; |
|
| − | + | po = treeToPreorder t ; |
|
| − | + | io = treeToInorder t } in preInTree po io >>= print |
|
Branch 'a' (Branch 'b' (Branch 'd' Empty Empty) (Branch 'e' Empty Empty)) (Branch 'c' Empty (Branch 'f' (Branch 'g' Empty Empty) Empty)) |
Branch 'a' (Branch 'b' (Branch 'd' Empty Empty) (Branch 'e' Empty Empty)) (Branch 'c' Empty (Branch 'f' (Branch 'g' Empty Empty) Empty)) |
||
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/68 | Solutions]] |
||
== Problem 69 == |
== Problem 69 == |
||
| + | <div style="border-bottom:1px solid #eee">Dotstring representation of binary trees. <span style="float:right"><small>[[99 questions/Solutions/69|Solutions]]</small></span> |
||
| − | |||
| + | </div> |
||
| − | Dotstring representation of binary trees. |
||
| + | <br> |
||
We consider again binary trees with nodes that are identified by single lower-case letters, as in the example of problem P67. Such a tree can be represented by the preorder sequence of its nodes in which dots (.) are inserted where an empty subtree (nil) is encountered during the tree traversal. For example, the tree shown in problem P67 is represented as 'abd..e..c.fg...'. First, try to establish a syntax (BNF or syntax diagrams) and then write a predicate tree_dotstring/2 which does the conversion in both directions. Use |
We consider again binary trees with nodes that are identified by single lower-case letters, as in the example of problem P67. Such a tree can be represented by the preorder sequence of its nodes in which dots (.) are inserted where an empty subtree (nil) is encountered during the tree traversal. For example, the tree shown in problem P67 is represented as 'abd..e..c.fg...'. First, try to establish a syntax (BNF or syntax diagrams) and then write a predicate tree_dotstring/2 which does the conversion in both directions. Use |
||
| Line 310: | Line 313: | ||
<haskell> |
<haskell> |
||
| − | > fst (ds2tree example) |
+ | λ> fst (ds2tree example) |
Branch 'a' (Branch 'b' (Branch 'd' Empty Empty) (Branch 'e' Empty Empty)) (Branch 'c' Empty (Branch 'f' (Branch 'g' Empty Empty) Empty)) |
Branch 'a' (Branch 'b' (Branch 'd' Empty Empty) (Branch 'e' Empty Empty)) (Branch 'c' Empty (Branch 'f' (Branch 'g' Empty Empty) Empty)) |
||
| − | > tree2ds (Branch 'x' (Branch 'y' Empty Empty) (Branch 'z' (Branch '0' Empty Empty) Empty)) |
+ | λ> tree2ds (Branch 'x' (Branch 'y' Empty Empty) (Branch 'z' (Branch '0' Empty Empty) Empty)) |
"xy..z0..." |
"xy..z0..." |
||
</haskell> |
</haskell> |
||
| − | |||
| − | [[99 questions/Solutions/69 | Solutions]] |
||
Latest revision as of 05:35, 11 June 2023
This is part of Ninety-Nine Haskell Problems, based on Ninety-Nine Prolog Problems.
Binary trees
As defined here.
An example tree:
tree4 = Branch 1 (Branch 2 Empty (Branch 4 Empty Empty))
(Branch 2 Empty Empty)
Problem 61
A leaf is a node with no successors. Write a predicate count_leaves/2 to count them.
Example:
% count_leaves(T,N) :- the binary tree T has N leaves
Example in Haskell:
λ> countLeaves tree4
2
Problem 61A
A leaf is a node with no successors. Write a predicate leaves/2 to collect them in a list.
Example:
% leaves(T,S) :- S is the list of all leaves of the binary tree T
Example in Haskell:
λ> leaves tree4
[4,2]
Problem 62
An internal node of a binary tree has either one or two non-empty successors. Write a predicate internals/2 to collect them in a list.
Example:
% internals(T,S) :- S is the list of internal nodes of the binary tree T.
Example in Haskell:
λ> internals tree4
[1,2]
Problem 62B
A node of a binary tree is at level N if the path from the root to the node has length N-1. The root node is at level 1. Write a predicate atlevel/3 to collect all nodes at a given level in a list.
Example:
% atlevel(T,L,S) :- S is the list of nodes of the binary tree T at level L
Example in Haskell:
λ> atLevel tree4 2
[2,2]
Problem 63
A complete binary tree with height H is defined as follows:
- The levels 1,2,3,...,H-1 contain the maximum number of nodes (i.e 2**(i-1) at the level i)
- In level H, which may contain less than the maximum possible number of nodes, all the nodes are "left-adjusted". This means that in a levelorder tree traversal all internal nodes come first, the leaves come second, and empty successors (the nil's which are not really nodes!) come last.
Particularly, complete binary trees are used as data structures (or addressing schemes) for heaps.
We can assign an address number to each node in a complete binary tree by enumerating the nodes in level-order, starting at the root with number 1. For every node X with address A the following property holds: The address of X's left and right successors are 2*A and 2*A+1, respectively, if they exist. This fact can be used to elegantly construct a complete binary tree structure.
Write a predicate complete_binary_tree/2.
Example:
% complete_binary_tree(N,T) :- T is a complete binary tree with N nodes.
Example in Haskell:
λ> completeBinaryTree 4
Branch 'x' (Branch 'x' (Branch 'x' Empty Empty) Empty) (Branch 'x' Empty Empty)
λ> isCompleteBinaryTree $ Branch 'x' (Branch 'x' Empty Empty) (Branch 'x' Empty Empty)
True
Problem 64
Given a binary tree as the usual Prolog term t(X,L,R) (or nil). As a preparation for drawing the tree, a layout algorithm is required to determine the position of each node in a rectangular grid. Several layout methods are conceivable, one of them is shown in the illustration below:
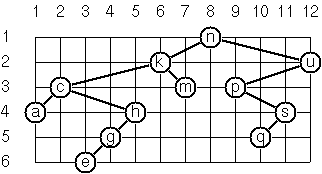
In this layout strategy, the position of a node v is obtained by the following two rules:
- x(v) is equal to the position of the node v in the inorder sequence
- y(v) is equal to the depth of the node v in the tree
Write a function to annotate each node of the tree with a position, where (1,1) in the top left corner or the rectangle bounding the drawn tree.
Here is the example tree from the above illustration:
tree64 = Branch 'n'
(Branch 'k'
(Branch 'c'
(Branch 'a' Empty Empty)
(Branch 'h'
(Branch 'g'
(Branch 'e' Empty Empty)
Empty
)
Empty
)
)
(Branch 'm' Empty Empty)
)
(Branch 'u'
(Branch 'p'
Empty
(Branch 's'
(Branch 'q' Empty Empty)
Empty
)
)
Empty
)
Example in Haskell:
λ> layout tree64
Branch ('n',(8,1)) (Branch ('k',(6,2)) (Branch ('c',(2,3)) ...
Problem 65
An alternative layout method is depicted in the illustration below:
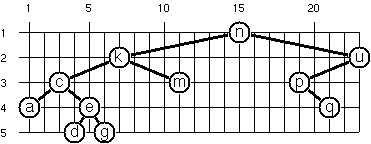
Find out the rules and write the corresponding function. Hint: On a given level, the horizontal distance between neighboring nodes is constant.
Use the same conventions as in problem P64 and test your function in an appropriate way.
Here is the example tree from the above illustration:
tree65 = Branch 'n'
(Branch 'k'
(Branch 'c'
(Branch 'a' Empty Empty)
(Branch 'e'
(Branch 'd' Empty Empty)
(Branch 'g' Empty Empty)
)
)
(Branch 'm' Empty Empty)
)
(Branch 'u'
(Branch 'p'
Empty
(Branch 'q' Empty Empty)
)
Empty
)
Example in Haskell:
λ> layout tree65
Branch ('n',(15,1)) (Branch ('k',(7,2)) (Branch ('c',(3,3)) ...
Problem 66
Yet another layout strategy is shown in the illustration below:
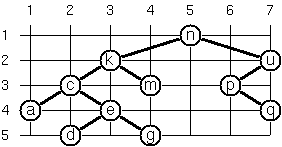
The method yields a very compact layout while maintaining a certain symmetry in every node. Find out the rules and write the corresponding Prolog predicate. Hint: Consider the horizontal distance between a node and its successor nodes. How tight can you pack together two subtrees to construct the combined binary tree?
Use the same conventions as in problem P64 and P65 and test your predicate in an appropriate way. Note: This is a difficult problem. Don't give up too early!
Which layout do you like most?
Example in Haskell:
λ> layout tree65
Branch ('n',(5,1)) (Branch ('k',(3,2)) (Branch ('c',(2,3)) ...
Problem 67A
Somebody represents binary trees as strings of the following type:
- a(b(d,e),c(,f(g,)))
a) Write a Prolog predicate which generates this string representation, if the tree is given as usual (as nil or t(X,L,R) term). Then write a predicate which does this inverse; i.e. given the string representation, construct the tree in the usual form. Finally, combine the two predicates in a single predicate tree_string/2 which can be used in both directions.
Example in Prolog
?- tree_to_string(t(x,t(y,nil,nil),t(a,nil,t(b,nil,nil))),S).
S = 'x(y,a(,b))'
?- string_to_tree('x(y,a(,b))',T).
T = t(x, t(y, nil, nil), t(a, nil, t(b, nil, nil)))
Example in Haskell:
λ> stringToTree "x(y,a(,b))" >>= print
Branch 'x' (Branch 'y' Empty Empty) (Branch 'a' Empty (Branch 'b' Empty Empty))
λ> let t = cbtFromList ['a'..'z'] in stringToTree (treeToString t) >>= print . (== t)
True
Problem 68
We consider binary trees with nodes that are identified by single lower-case letters, as in the example of Problem 67.
a) Write predicates preorder/2 and inorder/2 that construct the preorder and inorder sequence of a given binary tree, respectively. The results should be atoms, e.g. 'abdecfg' for the preorder sequence of the example in problem P67.
b) Can you use preorder/2 from problem part a) in the reverse direction; i.e. given a preorder sequence, construct a corresponding tree? If not, make the necessary arrangements.
c) If both the preorder sequence and the inorder sequence of the nodes of a binary tree are given, then the tree is determined unambiguously. Write a predicate pre_in_tree/3 that does the job.
Example in Haskell:
λ> let { Just t = stringToTree "a(b(d,e),c(,f(g,)))" ;
po = treeToPreorder t ;
io = treeToInorder t } in preInTree po io >>= print
Branch 'a' (Branch 'b' (Branch 'd' Empty Empty) (Branch 'e' Empty Empty)) (Branch 'c' Empty (Branch 'f' (Branch 'g' Empty Empty) Empty))
Problem 69
We consider again binary trees with nodes that are identified by single lower-case letters, as in the example of problem P67. Such a tree can be represented by the preorder sequence of its nodes in which dots (.) are inserted where an empty subtree (nil) is encountered during the tree traversal. For example, the tree shown in problem P67 is represented as 'abd..e..c.fg...'. First, try to establish a syntax (BNF or syntax diagrams) and then write a predicate tree_dotstring/2 which does the conversion in both directions. Use difference lists.
Example in Haskell:
λ> fst (ds2tree example)
Branch 'a' (Branch 'b' (Branch 'd' Empty Empty) (Branch 'e' Empty Empty)) (Branch 'c' Empty (Branch 'f' (Branch 'g' Empty Empty) Empty))
λ> tree2ds (Branch 'x' (Branch 'y' Empty Empty) (Branch 'z' (Branch '0' Empty Empty) Empty))
"xy..z0..."