Difference between revisions of "99 questions/70B to 73"
m (unify ghci prompts) |
m (→Problem 70) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 7: | Line 7: | ||
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest. |
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest. |
||
| − | https:// |
+ | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p70.gif |
== Problem 70B == |
== Problem 70B == |
||
| Line 72: | Line 72: | ||
By this rule, the tree below (<tt>tree5</tt>) is represented as: <tt>afg^^c^bd^e^^^</tt> |
By this rule, the tree below (<tt>tree5</tt>) is represented as: <tt>afg^^c^bd^e^^^</tt> |
||
| − | https:// |
+ | https://www.ic.unicamp.br/~meidanis/courses/mc336/2009s2/prolog/problemas/p70.gif |
Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. |
Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. |
||
Revision as of 22:52, 10 July 2021
This is part of Ninety-Nine Haskell Problems, based on Ninety-Nine Prolog Problems.
Multiway Trees
A multiway tree is composed of a root element and a (possibly empty) set of successors which are multiway trees themselves. A multiway tree is never empty. The set of successor trees is sometimes called a forest.
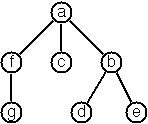
Problem 70B
(*) Check whether a given term represents a multiway tree.
In Prolog or Lisp, one writes a predicate to check this.
Example in Prolog:
?- istree(t(a,[t(f,[t(g,[])]),t(c,[]),t(b,[t(d,[]),t(e,[])])])). Yes
In Haskell, we define multiway trees as a datatype, as in the module Data.Tree:
data Tree a = Node a [Tree a]
deriving (Eq, Show)
Some example trees:
tree1 = Node 'a' []
tree2 = Node 'a' [Node 'b' []]
tree3 = Node 'a' [Node 'b' [Node 'c' []]]
tree4 = Node 'b' [Node 'd' [], Node 'e' []]
tree5 = Node 'a' [
Node 'f' [Node 'g' []],
Node 'c' [],
Node 'b' [Node 'd' [], Node 'e' []]
]
The last is the tree illustrated above.
As in problem 54A, all members of this type are multiway trees; there is no use for a predicate to test them.
Problem 70C
(*) Count the nodes of a multiway tree.
Example in Haskell:
λ> nnodes tree2
2
Problem 70
(**) Tree construction from a node string.
We suppose that the nodes of a multiway tree contain single characters. In the depth-first order sequence of its nodes, a special character ^ has been inserted whenever, during the tree traversal, the move is a backtrack to the previous level.
By this rule, the tree below (tree5) is represented as: afg^^c^bd^e^^^

Define the syntax of the string and write a predicate tree(String,Tree) to construct the Tree when the String is given. Make your predicate work in both directions.
Example in Haskell:
λ> stringToTree "afg^^c^bd^e^^^"
Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]]
λ> treeToString (Node 'a' [Node 'f' [Node 'g' []],Node 'c' [],Node 'b' [Node 'd' [],Node 'e' []]])
"afg^^c^bd^e^^^"
Problem 71
(*) Determine the internal path length of a tree.
We define the internal path length of a multiway tree as the total sum of the path lengths from the root to all nodes of the tree. By this definition, tree5 has an internal path length of 9.
Example in Haskell:
λ> ipl tree5
9
λ> ipl tree4
2
Problem 72
(*) Construct the bottom-up order sequence of the tree nodes.
Write a predicate bottom_up(Tree,Seq) which constructs the bottom-up sequence of the nodes of the multiway tree Tree.
Example in Haskell:
λ> bottom_up tree5
"gfcdeba"
Problem 73
(**) Lisp-like tree representation.
There is a particular notation for multiway trees in Lisp. Lisp is a prominent functional programming language, which is used primarily for artificial intelligence problems. As such it is one of the main competitors of Prolog. In Lisp almost everything is a list, just as in Prolog everything is a term.
The following pictures show how multiway tree structures are represented in Lisp.

Note that in the "lispy" notation a node with successors (children) in the tree is always the first element in a list, followed by its children. The "lispy" representation of a multiway tree is a sequence of atoms and parentheses '(' and ')', which we shall collectively call "tokens". We can represent this sequence of tokens as a Prolog list; e.g. the lispy expression (a (b c)) could be represented as the Prolog list ['(', a, '(', b, c, ')', ')']. Write a predicate tree_ltl(T,LTL) which constructs the "lispy token list" LTL if the tree is given as term T in the usual Prolog notation.
(The Prolog example given is incorrect.)
Example in Haskell:
λ> display lisp tree1
"a"
λ> display lisp tree2
"(a b)"
λ> display lisp tree3
"(a (b c))"
λ> display lisp tree4
"(b d e)"
λ> display lisp tree5
"(a (f g) c (b d e))"
As a second, even more interesting exercise try to rewrite tree_ltl/2 in a way that the inverse conversion is also possible.