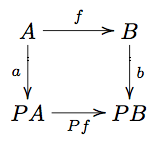User:Michiexile/MATH198/Lecture 9
IMPORTANT NOTE: THESE NOTES ARE STILL UNDER DEVELOPMENT. PLEASE WAIT UNTIL AFTER THE LECTURE WITH HANDING ANYTHING IN, OR TREATING THE NOTES AS READY TO READ.
Recursion patterns
Meijer, Fokkinga & Patterson identified in the paper Functional programming with bananas, lenses, envelopes and barbed wire a number of generic patterns for recursive programming that they had observed, catalogued and systematized. The aim of that paper is to establish a number of rules for modifying and rewriting expressions involving these generic recursion patterns.
As it turns out, these patterns are instances of the same phenomenon we saw last lecture: where the recursion comes from specifying a different algebra, and then take a uniquely existing morphism induced by initiality (or, as we shall see, finality).
Before we go through the recursion patterns, we need to establish a few pieces of theoretical language, dualizing the Eilenberg-Moore algebra constructions from the last lecture.
Coalgebras for endofunctors
Definition If is an endofunctor, then a -coalgebra on is a morphism .
A morphism of coalgebras: is some such that the diagram
commutes.
Just as with algebras, we get a category of coalgebras. And the interesting objects here are the final coalgebras. Just as with algebras, we have
Lemma (Lambek) If is a final coalgebra, it is an isomorphism.
Finally, one thing that makes us care highly about these entities: in an appropriate category (such as ), initial algebras and final coalgebras coincide, with the correspondence given by inverting the algebra/coalgebra morphism. In Haskell not quite true (specifically, the final coalgebra for the lists functor gives us streams...).
Onwards to recursion schemes!
We shall define a few specific morphisms we'll use repeatedly. This notation, introduced here, occurs all over the place in these corners of the literature, and are good to be aware of in general:
- If is an initial algebra for , we denote .
- If is a final coalgebra for , we denote .
- We write for the fixed point operator
mu f = x where x = f x
- MFP write for
Delta f g = \x -> (f x, g x)
- MFP write for
(Nabla f g) (Left x) = f x
(Nabla f g) (Right x) = g x
These two last constructions are directly motivated by the maps induced from the universal properties of products and coproducts.
We shall write and for the and constructions, respectively.
We note that in the situation considered by MFP, inital algebras and final coalgebras coincide, and thus are the pair of isomorphic maps induced by either the initial algebra- or the final coalgebra-structure.
Catamorphisms
A catamorphism is the uniquely existing morphism from an initial algebra to a different algebra. We have to define maps down to the return value type for each of the constructors of the complex data type we're recursing over, and the catamorphism will deconstruct the structure (trees, lists, ...) and do a generalized fold over the structure at hand before returning the final value.
The intuition is that for catamorphisms we start essentially structured, and dismantle the structure.
Example: the length function from last lecture. This is the catamorphism for the functor given by the maps
u :: Int
u = 0
m :: (A, Int) -> Int
m (a, n) = n+1
MFP define the catamorphism by, supposing T is initial for the functor F:
cata :: (F a b -> b) -> T a -> b
cata phi = mu (\x -> phi . fmap x . outT)
We can reframe the example above as a catamorphism by observing that here,
data F a b = Nil | Cons a b deriving (Eq, Show)
type T a = [a]
instance Functor (F a) where
fmap _ Nil = Nil
fmap f (Cons n a) = Cons n (f a)
outT :: T a -> F a (T a)
outT [] = Nil
outT (a:as) = Cons a as
lphi :: F a Int -> Int
lphi Nil = 0
lphi (Cons a n) = n + 1
l = cata lphi
where we observe that mu has a global definition for everything we do and out is defined once we settle on the functor F and its initial algebra. Thus, the definition of phi really is the only place that the recursion data shows up.
Anamorphisms
An anamorphism is the categorical dual to the catamorphism. It is the canonical morphism from a coalgebra to the final coalgebra for that endofunctor.
Here, we start unstructured, and erect a structure, induced by the coalgebra structures involved.
Example: we can write a recursive function
first :: Int -> [Int]
first 1 = [1]
first n = n : first (n - 1)
This is an anamorphism from the coalgebra for on generated by the two maps
c 0 = Left ()
c n = Right (n, n-1)
and we observe that we can chase through the diagram
to conclude that therefore
f 0 = []
f n = n : f (n - 1)
which is exactly the recursion we wrote to begin with.
MFP define the anamorphism by a fixpoint as well, namely:
ana :: (b -> F a b) -> b -> T a
ana psi = mu (\x -> inT . fmap x . psi)
We can, again, recast our illustration above into a structural anamorphism, by:
-- Reuse mu, F, T from above
inT :: F a (T a) -> T a
inT Nil = []
inT (Cons a as) = a:as
fpsi :: Int -> F Int Int
fpsi 0 = Nil
fpsi n = Cons n (n-1)
Again, we can note that the implementation of fpsi here is exactly the c above, and the resulting function will - as we can verify by compiling and running - give us the same kind of reversed list of the n first integers as the first function above would.
Hylomorphisms
The hylomorphisms capture one of the two possible compositions of anamorphisms and catamorphisms. Parametrized over an algebra and a coalgebra the hylomorphism is a recursion pattern that computes a value in from a value in by generating some sort of intermediate structure and then collapsing it again.
It is, thus the composition of the uniquely existing morphism from a coalgebra to the final coalgebra for an endofunctor, followed by the uniquely existing morphism from the initial algebra to some other algebra.
MFP define it, again, as a fix point:
hylo :: (F a b2 -> b2) -> (b1 -> F a b1) -> b1 -> b2
hylo phi psi = mu (\x -> phi . fmap x . psi)
First off, we can observe that by picking one or the other of as a parameter, we can recover both the anamorphisms and the catamorphisms as hylomorphisms.
As an example, we'll compute the factorial function using a hylomorphism:
phi :: F Int Int -> Int
phi Nil = 1
phi (Cons n m) = n*m
psi :: Int -> F Int Int
psi 0 = Int
psi n = Cons n (n-1)
factorial = hylo phi psi
Metamorphisms
The metamorphism is the other composition of an anamorphism with a catamorphism. It takes some structure, deconstructs it, and then reconstructs a new structure from it.
As a recursion pattern, it's kinda boring - it'll take an interesting structure, deconstruct it into a scalar value, and then reconstruct some structure from that scalar. As such, it won't even capture the richness of , since any morphism expressed as a metamorphism will factor through a map .
Paramorphisms
Paramorphisms were discussed in the MFP paper as a way to extend the catamorphisms so that the operating function can access its arguments in computation as well as in recursion. We gave the factorial above as a hylomorphism instead of a catamorphism precisely because no simple enough catamorphic structure exists.
Apomorphisms
The apomorphism is the dual of the paramorphism - it does with retention of values along the way what anamorphisms do compared to catamorphisms.
Further reading
Terminology in the literature: in and out, inl, inr. Bananas et.c. Sorting morphisms.
Homework
- Write a fold for the data type
data T a = L a | B a a | C a a aand demonstrate how this can be written as a catamorphism by giving the algebra it maps to. - Write the fibonacci function as a hylomorphism.
- Write the Towers of Hanoi as a hylomorphism. You'll probably want to use binary trees as the intermediate data structure.
- Write a prime numbers generator as an anamorphism.
- * The integers have a partial order induced by the divisibility relation. We can thus take any integer and arrange all its divisors in a tree by having an edge if and doesn't divide any other divisor of . Write an anamorphic function that will generate this tree for a given starting integer. Demonstrate how this function is an anamorphism by giving the algebra it maps from.
- Hint: You will be helped by having a function to generate a list of all primes. One suggestion is:
primes :: [Integer]
primes = sieve [2..]
where
sieve (p:xs) = p : sieve [x|x <- xs, x `mod` p > 0]
- Hint: A good data structure to use is; with expected output of running the algorithm:
data Tree = Leaf Integer | Node Integer [Tree]
divisionTree 60 =
Node 60 [
Node 30 [
Node 15 [
Leaf 5,
Leaf 3],
Node 10 [
Leaf 5,
Leaf 2],
Node 6 [
Leaf 3,
Leaf 2]],
Node 20 [
Node 10 [
Leaf 5,
Leaf 2],
Node 4 [
Leaf 2]],
Node 12 [
Node 6 [
Leaf 3,
Leaf 2],
Node 4 [
Leaf 2]]]